머신 러닝 모델은 학습데이터로부터 특정한 패턴을 학습합니다. 그리고 학습된 모델의 성능은 테스트 데이터를 이용하여 측정됩니다. 모델의 일반화 성능은 validation dataset 을 이용한 성능 테스트를 통하여 측정됩니다. 우리는 주로 모델의 학습 과정은 training, test dataset 을 이용한 과정으로 정의합니다. 하지만 사실은 validation dataset 을 이용하여 성능이 가장 좋은 “모델을 선택”하는 과정까지도 학습에 포함됩니다. 사실 우리는 cherry picking 을 하고 있습니다. 이번 포스트에서는 모델의 학습 과정에서 우리가 행하는 cherry picking 의 과정과 그 위험성에 대한 선배의 세미나의 내용을 기록하였습니다.
우리는 정말로 over-fitting 을 예방하는가?
며칠 전 금융권에서 시장 예측 모델링을 하는 선배의 세미나를 들을 수 있었습니다. 세미나의 내용은 시장을 예측하는 것이 얼마나 어려운지에 대한 내용이었습니다. 놀랍게도 금융 시장을 예측하는 모델들의 up/down 예측력은 51 ~ 52 % 정도이면 매우 훌륭한 모델들이라고 합니다. 하지만 많은 논문들에 적혀있는 성능들이 60 % 을 넘는 경우도 많습니다. 선배의 표현을 그대로 옮겨보자면, “그런 수치를 적는 것은 사기이거나, 본인이 무슨 말을 하는지 모르면서 하는 말”이라 했습니다. 왠지 속이 시원해지는 말이었습니다.
그렇다면 왜 논문들에서는 현실적이지 않는 성능을 기재하는 것일까요? 그 이유에 대한 설명이 인상깊어서 꼭 포트스로 적어둬야겠다는 생각을 했습니다.
모델을 학습하기 위하여 데이터셋을 세 종류, Training / Testing / Validation dataset 로 나눠 이용합니다. Training dataset 을 이용하여 모델들의 parameters 를 학습합니다. Testing dataset 은 모델을 학습 할 때 over-fitting 을 방지하는 용도로 이용됩니다. 또한 neural network 의 hidden layers 의 구조를 바꾼다던지, tree 계열이나 support vector 를 이용하는 모델들을 선택하는 것처럼 여러 모델 중에 예측력이 좋은 모델을 고르는데도 이용됩니다. 최종적으로 Validation dataset 을 이용하여 “가장 좋은 일반화 성능을 지니는 모델을 선택”합니다. Training 과 testing 과정을 분리한 것은 모델이 training dataset 에 over-fitting 되는 것을 방지하기 위함입니다. 그리고 testing 과 validation 과정을 분리한 것은 testing dataset 에 독립적인 성능을 측정하기 위해서입니다. 그런데 validation 과정을 거쳐 최종적으로 모델을 선정한다면 결국 validation dataset 에 over-fitting 된 하나의 모델을 “학습한 것”입니다. 모델의 선택도 학습입니다. 우리는 validation 을 통하여 validation dataset 에 적합한 모델을 cherry picking 하였습니다. Cherry picking 은 모델의 결과 중에서 좋은 것들만 골라 소개하는 행위를 일컫는 말입니다.
일반화 성능의 측정은 unseen data 에서의 예측 능력을 평가하기 위함입니다. \(X\) 에서 \(Y\) 로의 관계를 모델이 학습하는 추상화된 공식으로 학습하여 학습과정에서 보지 못했던 \(X\) 를 추론합니다. \((X, Y)\) 에 변동이 생겼을 때에도 적용이 될 수 있는 규칙은 주로 복잡하다기보다는 직관적이고 논리적이며 납득할 수 있는 규칙일 것입니다. 비슷한 성능을 보이는 모델이라면 단순한 모델을 선택하자는 Occam’s razor 를 따라야 하는 이유입니다.
선배는 “금융 시장에서의 모델의 성능은 장기적인 적용을 통해서만 제대로 평가될 수 있으며, 테스트는 모델이 적용되는 바로 그 시점 단 한 번” 이라고 말해줬습니다. 저는 그동안 모델의 성능 평가를 얼마나 깐깐하게 따지며 했던가 되돌아 보았습니다.
Cherry picking distort distribution
선배가 들어줬던 cherry picking 의 위험성을 설명하는 실험이 너무나 명료하고 인상 깊어, 실험 코드와 결과를 공유합니다.
매우 간단한 실험입니다. 평균 0, 표준 편차 1 을 따르는 정규분포, \(N(0, 1)\) 로부터 1000 개의 samples 을 임의로 생성합니다. 그리고 samples 의 분포를 살펴보면 평균 0, 표준 편차 1 을 따르는 정규분포를 따릅니다. 이번에는 10 개의 sampels 를 \(N(0, 1)\) 로부터 추출한 뒤, 이 중 최대값을 하나의 sample 로 이용합니다. 이 행위를 1000 번 반복하여 1000 개의 samples 를 만듭니다. 이 samples 의 분포는 평균이 0 보다 크고 표준 편차가 1보다 작은, 평행 이동 된 정규 분포입니다. 이번에는 \(N(0, 1)\) 로부터 30 개의 samples 중 최대값을 하나의 sample 로 이용합니다. 10 개로부터 추출한 samples 의 최대값보다 더 shifted 된 정규 분포를 얻을 수 있습니다.
이는 \(s\) 개의 samples 에서의 최대값의 확률 분포를 직접 구해서 살펴보아도 됩니다. 우리는 실험을 통하여 살펴봅시다.
max_random_sample 은 \(N(0, 1)\) 로부터 max_from 개의 samples 을 만든 뒤, 이의 최대값을 return 하는 함수입니다.
import numpy as np
def max_random_sample(max_from=1):
# mean, std, n samples
return np.random.normal(0, 1, max_from).max()max_random_samples 는 max_random_sample 로부터 n_samples 의 samples 을 얻는 함수입니다.
def max_random_samples(max_from, n_samples):
return np.asarray(
[max_random_sample(max_from) for _ in range(n_samples)])Bokeh 를 이용하여 histrogram 을 plotting 할 준비를 합니다. brewer 는 histogram 의 색을 이용하기 위한 palette 입니다. bokeh.plotting.figure.quad 를 이용하면 histogram 을 그릴 수 있습니다. alpha 는 각 bar 의 투명도입니다.
from bokeh.plotting import show, output_notebook, output_file, figure
from bokeh.palettes import brewer
output_notebook()
def draw_histogram(bins, ranges, color="#036564", legend=None):
if not legend:
p.quad(top=bins, bottom=0, left=ranges[:-1], right=ranges[1:],
fill_color=color, line_color=color, alpha=0.5)
else:
p.quad(top=bins, bottom=0, left=ranges[:-1], right=ranges[1:],
fill_color=color, line_color=color, alpha=0.5, legend=legend)이제 실험을 진행합니다. 각각 1, 20, 50, 100, 200 개의 samples 로부터 최대값을 얻습니다. 이를 10000 번 반복합니다.
numpy.histogram 을 이용하면 sampels 를 equal width 로 bins 개 만큼의 hsitrogram 으로 나눠줍니다. bins 에는 각 bar 의 빈도수가 포함되어 있습니다. 이를 n_samples 로 나눠 각 bin 의 확률을 계산합니다. ranges 는 bins + 1 크기의 numpy.ndarray 입니다. histogram 의 begin, end 가 저장되어 있습니다.
p = figure()
n_samples = 10000
max_froms = [1, 20, 50, 100, 200]
colors = reversed(brewer['YlGnBu'][len(max_froms)])
for max_from, color in zip(max_froms, colors):
samples = max_random_samples(max_from, n_samples)
bins, ranges = np.histogram(samples, bins=30)
bins = bins / n_samples
legend = 'max from {} samples'.format(max_from)
draw_histogram(bins, ranges, color, legend)
mean = samples.mean()
std = samples.std()
print('max from {} samples: mean = {}, std = {}'.format(
max_from, '%.3f' % mean, '%.3f' % std))
show(p)위 실험을 통하여 얻은 평균과 표준편차 입니다. 더 많은 samples 에서 최대값을 취할수록 평균은 커지고 표준편차는 줄어듭니다.
max from 1 samples: mean = -0.014, std = 0.996
max from 20 samples: mean = 1.869, std = 0.527
max from 50 samples: mean = 2.251, std = 0.470
max from 100 samples: mean = 2.505, std = 0.425
max from 200 samples: mean = 2.746, std = 0.403
아래는 histogram 입니다. 더 많은 samples 에서 cherry picking 을 할수록 samples 의 확률 분포를 왜곡할 수 있습니다.
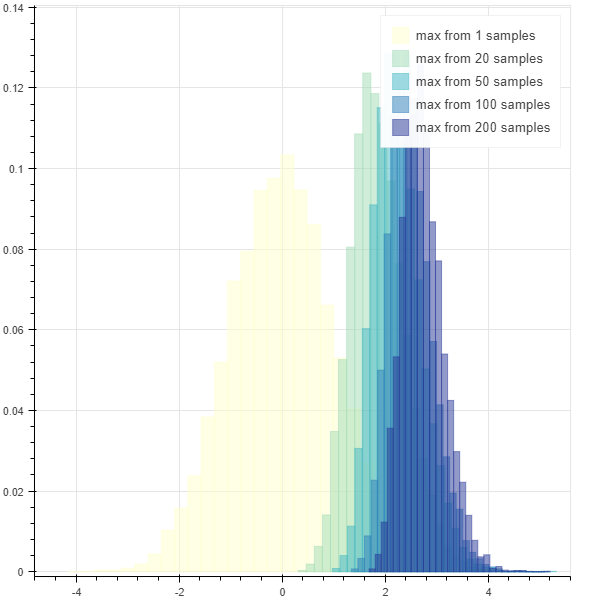
논문의 재현성
아래의 이야기는 일종의 check list 입니다. 세미나로부터 고민했던 생각들을 잊지 않기 위해 적어둡니다.
선배의 세미나에서도 제기된 문제이고, 실제로 머신 러닝 모델을 학습하는 사람이라면 모두가 동의할 말이라 생각합니다. 성능이 좋다고 제안된 논문을 나의 데이터에 적용하면 제대로 성능이 나오는 일이 드뭅니다. 이유는 다양합니다. Unseen 에 대한 테스트를 하여야 하는데, testing 이 training dataset 의 암기력만을 테스팅 하는 경우도 있습니다. 혹은 제안된 모델이 해당 논문의 데이터에 아주 적합하게 설계된 구조일 수도 있습니다. 혹은 test dataset 이 전체 패턴의 극히 일부일 수도 있습니다. 부분적인 (쉬운) 패턴에 대하여 학습과 평가를 한 것이라면 일반적인 성능이라 말할 수 없습니다. 특히 이미 학습된 상태로 배포되는 모델이라면 학습 데이터와 모델이 적용될 데이터에서의 distribution 이 차이가 많이 나는 경우일 수도 있습니다. 자연어처리에서는 이로부터 out of vocabulary problems 이 발생합니다.
그래서 특정 모델이 특정 데이터에 적용되어 얼마의 성능이 나왔다 라는 말보다, “왜 잘 작동하는지, 어떤 단점이 있을 수 있는지”를 알려주는 것이 중요하다 생각합니다.
모델의 구조도 data distribution 이 달라졌을 때에 이를 반영할 수 있거나, 사용자에 의하여 calibration 이 손쉽게 될 수 있는 형태로 설계되어야 한다고 생각합니다. 그렇기 때문에 모델의 해석과 사용자에 의한 간섭이 중요하다 생각합니다.
True unseen
세미나를 들으며 “어떤 문제에 unseen query 에 대한 깐깐한 테스트를 설계해야 하는가?”에 대해 고민했습니다. 금융 분야에서의 시장 예측은 이전의 데이터가 반복되지 않을 때가 많을 것입니다. 금융 만큼 복잡한 분야도 없을 것입니다. 세상의 모든 일이 엮여있어 모델에 영향을 줄 변수들이 너무나 많습니다. 상황을 설명하기에 충분한 변수들을 모으지 못한 것일수도 있습니다. 이때는 테스트 과정을 정말 깐깐하게 설계해야 할 것 입니다. Training 과정에 정말로 이용되지 않은 \(X\) 를 따로 떼어놓아야 할 수도 있습니다. 시계열적인 데이터라면 한 시점의 데이터는 모델의 학습 과정에 전혀 이용하지 않기도 해야할 것이고, 예외적인 상황에 대한 성능 측정도 고려해야 할 것입니다.
어떤 문제는 \(X\) 라는 input 에 \(y\) 라는 label 이 반복적으로 발생하고, 우리가 풀어야 하는 문제는 이전과 비슷한 \(X\) 에 대하여 \(y\) 를 예측 (정확히는 분류)하는 것이라면 training dataset 과 testing, validation dataset 의 분포를 일정하게 맞춰서 \((X, y\) 의 패턴을 “잘 외우는지” 측정해야 합니다.
일반화 성능의 측정은 문제에 따라 true unseen 상황을 가정해야 할 때도 있고, 그렇지 않을 때도 있습니다.
한 가지 더, 앞서 언급한 것처럼 test dataset 이 cover 하는 상황이 전체의 얼마가 되는지도 중요합니다. 발생할 수 있는 \(X\) 에 대하여 확신할 수 있는 \(X\) 의 양을 측정할 수 있다면 모델의 안정성, 신뢰성을 이야기 할 수 있습니다.