Scikit learn 의 logistic regression 이 더 좋은 solution 이 있음에도 이를 찾지 못할 수도 있다는 예시를 발견하였습니다. 이 실험을 통하여 어떤 solution 이 Softmax regression 의 더 좋은 solution 인지에 대한 논의도 함께 합니다.
Brief review of Softmax Regression
Softmax regression 은 가장 간단한 multi class classifiers 중 하나입니다. 클래스의 개수가 2 개일 때는 logistic regression classifier 라 부릅니다. Softmax regression 은 각 클래스의 대표벡터를 에 학습합니다.
각 클래스의 대표벡터가 클래스 별 데이터의 평균벡터는 아닙니다. Softmax regression dms 아래의 확률 공식에 가장 잘 맞는 를 학습합니다.
이에 대한 자세한 내용은 이전의 Logistic regression post 을 보시기 바랍니다. 이전 포스트를 작성하면서 5 개 클래스를 지닌 2 차원 인공데이터를 만들었습니다. 그리고 class 별로 공간을 잘 나눠 분포 되어 있을 때에는 대표벡터가 클래스 공간 위에 위치했지만, 두번째와 세번째 데이터처럼 공간의 한쪽에만 모든 클래스가 위치하면 빈 공간의 경계에 있는 클래스의 대표벡터가 한쪽으로 밀려나는 현상을 발견하였습니다. 저는 이 solutions 이 Softmax regression 알고리즘이 학습하는 cost function 기준으로 비용이 가장 작은 solutions 이라고 생각하였습니다.
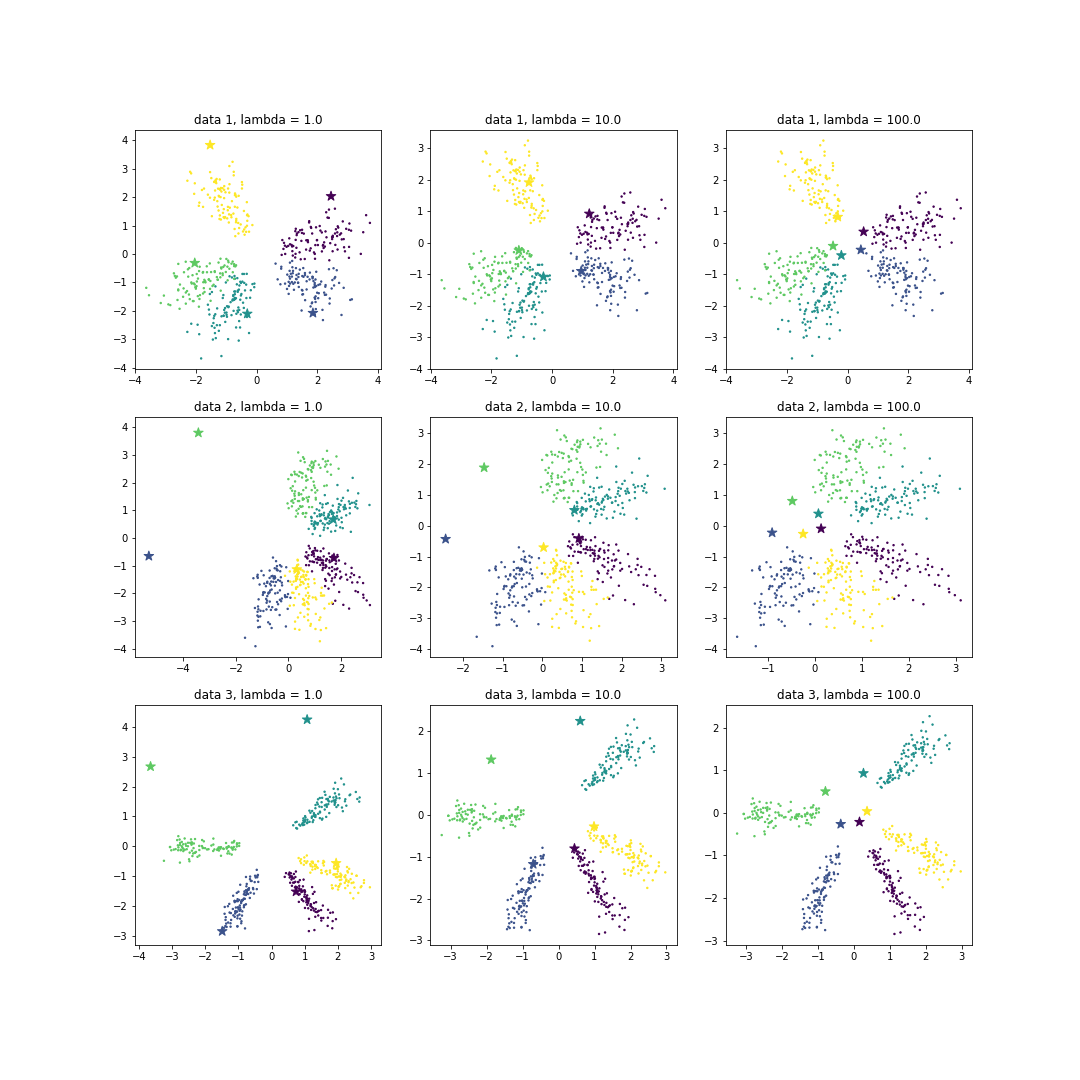
그런데, 정말로 저 solutions 이 optima 인지 궁금해졌습니다.
Not optimal solutions?
Softmax regression 의 cost 는 loss 와 regularization cost 의 합으로 정의됩니다. loss 는 학습데이터의 를 이용하여 를 예측하는 정확도에 관련된 부분이며, 이는 cross entropy 입니다. L2 regularization 을 이용할 경우에는 의 L2 norm 의 배 만큼의 비용이 듭니다.
Scikit learn 의 LogisticRegression 의 argument C 는 입니다.
class sklearn.linear_model.LogisticRegression(
penalty=’l2’,
dual=False,
tol=0.0001,
C=1.0,
fit_intercept=True,
intercept_scaling=1,
class_weight=None,
random_state=None,
solver=’liblinear’,
max_iter=100,
multi_class=’ovr’,
verbose=0,
warm_start=False,
n_jobs=1)
C 를 기본값 1 로 설정하여 모델을 학습한 뒤의 를 확인하였습니다. Star marker 는 같은 색의 클래스 데이터에 대한 입니다. 빈 공간이 경계에 위치한 클래스들의 대표 벡터는 빈 공간쪽으로 몰려있습니다. 그렇기 때문에 대표성을 띄는 좋은 벡터인지 의심이 듭니다.
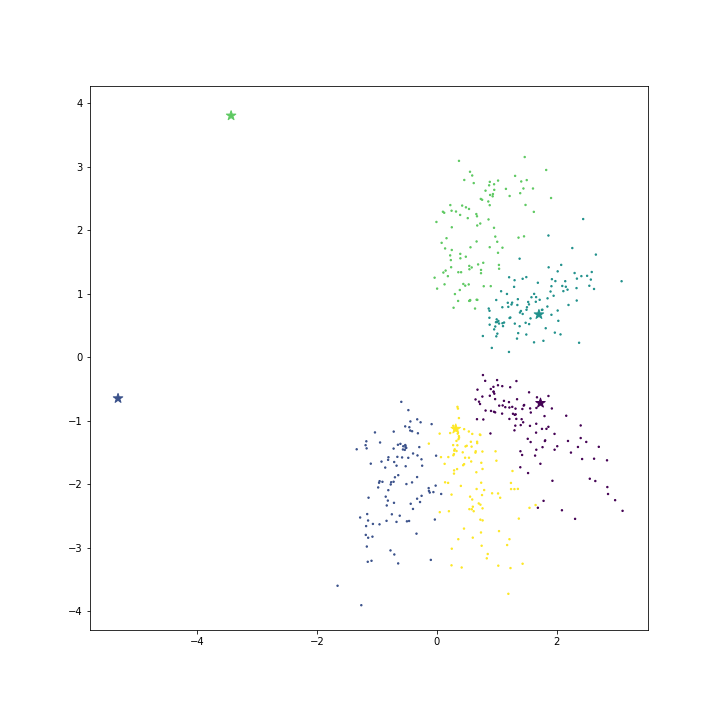
위의 cost function 공식을 이용하여 직접 loss 와 cost 를 계산하였습니다. 위 그림의 loss 와 cost 는 각각 loss = -0.729, cost=14.637 입니다.
import numpy as np
# cross entropy of softmax
def get_loss(X, class_vector):
exp = np.exp(np.inner(X, class_vector))
softmax = exp.max(axis=1) / exp.sum(axis=1)
loss = - softmax.sum() / X.shape[0]
return loss
# cost = loss + regularity
def get_cost(loss, coef, C):
cost = loss + 1/C * np.sqrt((coef ** 2).sum(axis=1)).sum()
return cost아래 그림은 모델을 학습시키지 않고, 각 클래스의 평균 벡터와 배수를 취한 벡터를 대표 벡터로 이용한 경우입니다.
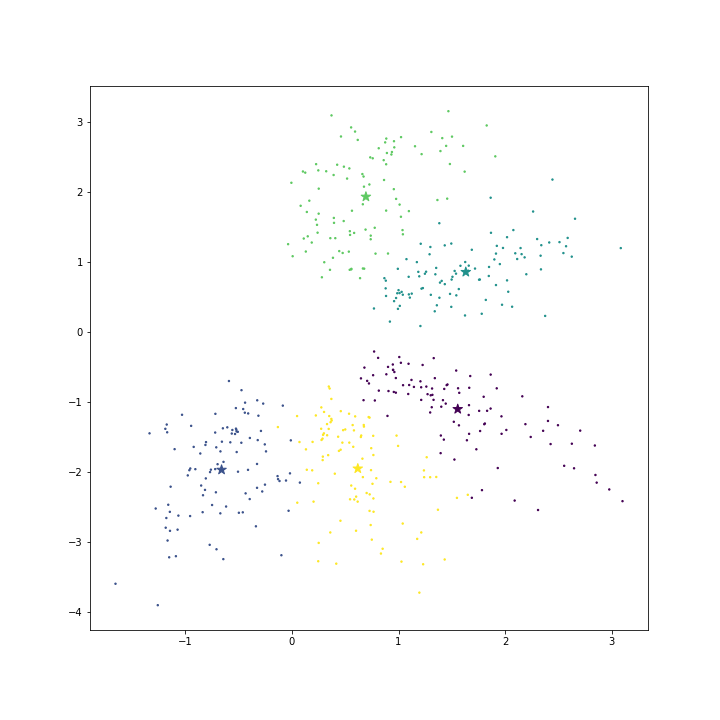
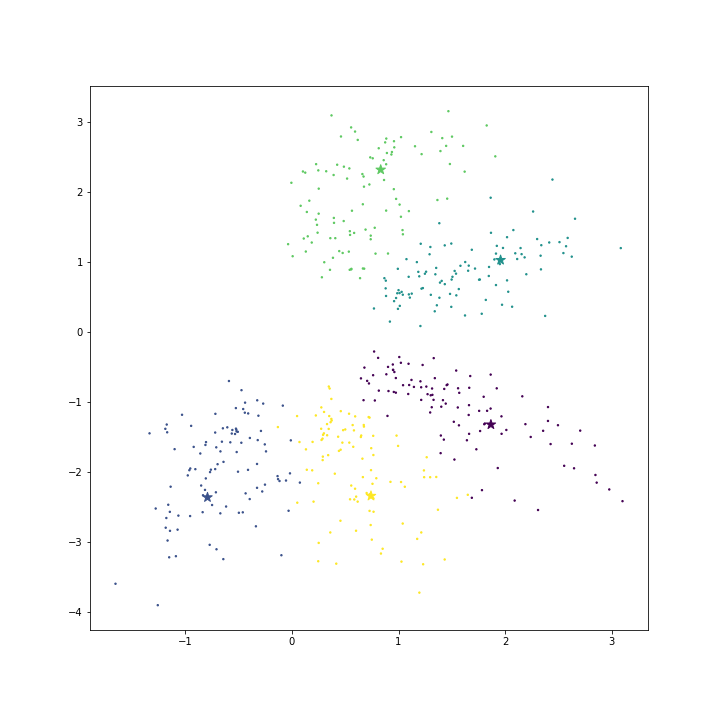
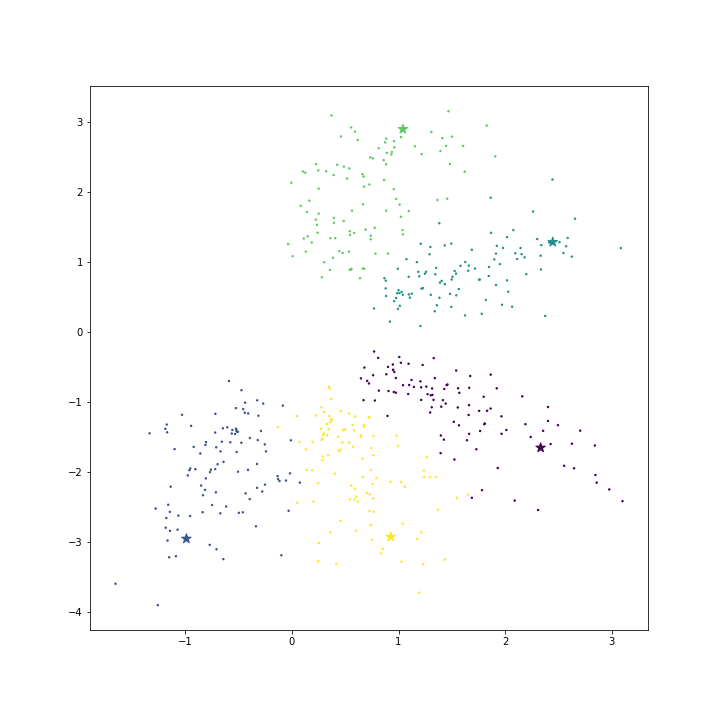
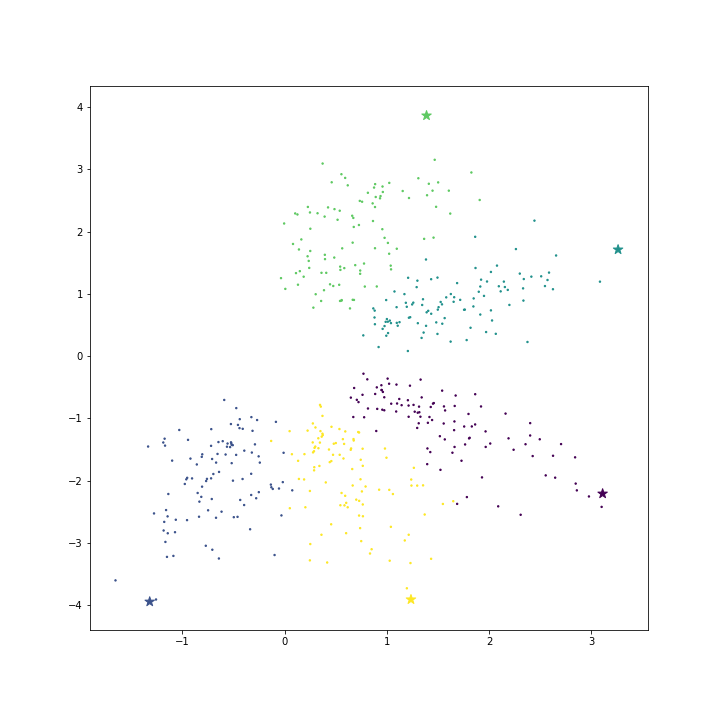
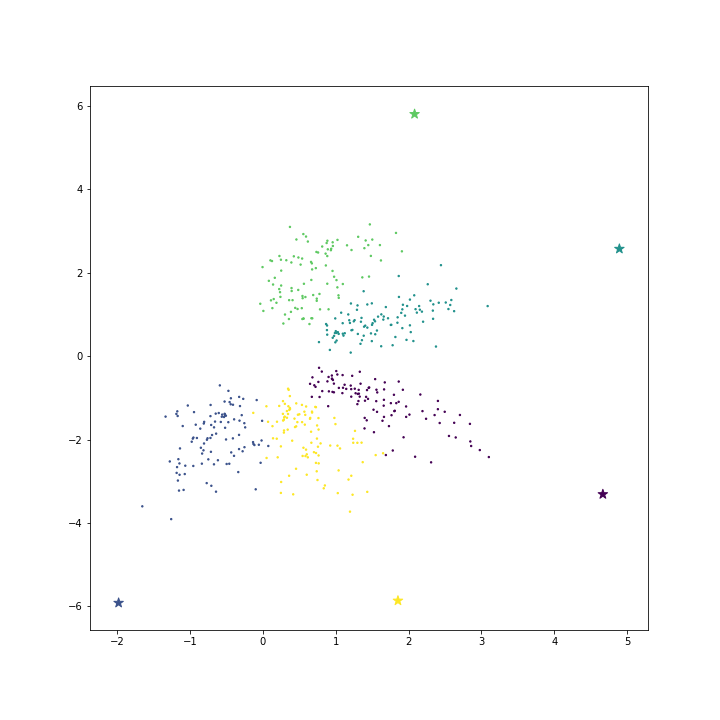
아래 표는 각각의 loss 와 cost 입니다. mean vector 를 로 이용하면 loss 모델을 학습하는 경우보다 loss 가 큽니다. 하지만 x1.5 ~ x2 배수를 취하면 loss 는 오히려 모델을 학습하는 경우보다도 작습니다. 모델의 학습은 cost 기준이기 때문에 mean vector 만을 이용하여도 cost 기준에서 훨씬 좋은 solution 입니다. 그런데 scikit learn 의 LogisticRegression 은 이와 다른 solution 을 찾았네요.
| Class vector type | loss | cost |
|---|---|---|
| model fit | -0.729 | 14.637 |
| mean vector | -0.613 | 9.318 |
| mean x 1.2 | -0.653 | 11.265 |
| mean x 1.5 | -0.702 | 14.195 |
| mean x 2 | -0.764 | 19.099 |
| mean x 3 | -0.842 | 28.952 |
위 표에서 알 수 있는 점 중 하나는, mean vector 에 x2 배수를 취한 경우보다 x3 배수를 취하면 loss 가 작습니다. 하지만, 의 크기가 커집니다. 그래서 cost 는 매우 커집니다. 벡터의 내적은 cosine norm 이기 때문에 큰 벡터일수록 극단적인 prediction 을 합니다. 위 예시의 데이터는 매우 깔끔한 형태이기 때문에 과적합 (over fitting) 의 느낌이 적지만, 복잡한 데이터의 경우에는 잘못된 학습을 할 수 있습니다. 그렇기 때문에 L2 regularization 을 합니다.
는 loss 와 regularity 사이에서 중요도를 정의하는 페러매터입니다. Accuracy 와 over fitting 사이에서 고민하며 의 모습을 결정합니다. 혹시 에 의한 영향인가 싶어 C 를 바꿔가며 모델을 학습했습니다만 solution 이 같았습니다.
어쩌면 solver 때문일지도 모르겠습니다. Solver 는 solution 을 찾는 알고리즘입니다 scikit-learn 의 LogisticRegression 에서 이용할 수 있는 solver 는 아래와 같습니다. Default 는 liblinear 입니다. 이들을 모두 바꿔가며 학습해도 그 결과가 같았습니다.
{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}
어쩌면 다른 seeds 를 이용하여 initialize 하면 다른 결과가 나올지도 모르겠습니다. random_state 를 모두 바꿔가며 실험하였지만, 이마저도 결과가 같았습니다. 모두 같은 solutions 을 찾았습니다.
for r in [5, 5985, 23230, 355, 9864943]
logistic = LogisticRegression(C=1, tol=0.0000001, random_state=r)
random_state=r코드를 뜯어서 내부를 살펴본 것은 아닙니다만, 의심되는 요인들을 바꿔 학습하여도 그 결과는 같았습니다. 이유를 알려면 코드를 뜯어봐야 할 것 같습니다.
Better solution?
이 실험을 하며, 더 좋은 solution 에 대하여 고민하였습니다. 모델이 학습한 solution 을 로 이용하여도 test data 에서 높은 정확도가 나옵니다. 하지만 벡터의 해석 측면에서 좋은 solution 이라고는 생각되지 않습니다.
그러나 평균 벡터를 취하는 것이 좋은 방법도 아닙니다. 예시로 이용한 toy data 는 prediction 을 못하면 절대 안되는 최하 난이도의 데이터입니다. 쉬운 문제이기 때문에 평균 벡터를 이용할 수 있으며, 각 클래스 별로 복잡한 모양을 지녔거나, 클래스 별로 서로 다른 밀도, 서로 다른 개수의 데이터들이 존재할 때도 반드시 잘 작동한다 보장할 수 없습니다.
그렇다면 어떻게하여야 해석력까지 줄 수 있는 better solution 을 구할 수는 없을까요? 일단 “Better” 에 대한 기준이 필요해 보입니다. 이 주제로 한 번 정도 더 포스팅을 할 예정입니다.