인공 데이터는 머신러닝 알고리즘의 작동 원리를 이해하는데 도움이 됩니다. Scikit-learn 에서는 two moons, swiss-roll 등 유명한 인공 데이터를 만드는 함수를 제공합니다. 그러나 scikit-learn 에서 제공하는 함수는 머신러닝 알고리즘이 풀기 쉬운 단순한 모양의 데이터만을 만들기에 몇 개의 인공 데이터 생성 함수를 만들었습니다. 이 포스트에서 소개하는 인공 데이터를 만드는 함수들은 github 에 공개하였습니다.
Motivation
이전 포스트에서 scikit-learn 의 함수를 이용하여 swiss roll data 를 만드는 이야기를 하였습니다.
from sklearn.datasets import make_swiss_roll
X, t = make_swiss_roll(n_samples=1000, noise=0)Plotly 를 이용하여 직접 생성한 swiss roll 을 시각화하는 이야기도 하였습니다.
위 그림의 swiss roll 은 1.5 바퀴 롤이 말려있는 형태입니다. 사실 이 데이터는 많은 manifold learning 알고리즘들이 잘 풀 수 있는 쉬운 난이도의 데이터셋입니다. 저는 더 복잡한 인공데이터를 만들고 싶습니다. 롤을 3 바퀴 혹은 4 바퀴 말거나, y 축의 width 를 넓게도 좁게도 만들고 싶습니다. scikit-learn 의 github 에서 make_swiss_roll 함수는 생각보다 간단합니다. 우리가 원하는 모양의 데이터를 만들기 위해 이를 수정하는 것은 어렵지 않습니다.
def make_swiss_roll(n_samples=100, noise=0.0, random_state=None):
"""docstring
.....
"""
generator = check_random_state(random_state)
t = 1.5 * np.pi * (1 + 2 * generator.rand(1, n_samples))
x = t * np.cos(t)
y = 21 * generator.rand(1, n_samples)
z = t * np.sin(t)
X = np.concatenate((x, y, z))
X += noise * generator.randn(3, n_samples)
X = X.T
t = np.squeeze(t)
return X, t귀찮을 뿐입니다. 그리고 이전에도 다양한 모양의 swiss roll 을 만드는 함수를 만들었었는데, 잃어버렸네요. 분명 제 컴퓨터인데 컴퓨터 속 코드를 잃어버리다니.. 이번에는 만든 함수는 정리해서 git 에 올려야겠다는 생각을 했습니다. 구현된 몇 가지 인공 데이터 생성 함수에 대한 예시와 parameters 를 정리하였습니다.
soydata
github 의 soydata 에는 현재 두 종류의 함수들이 있습니다. 첫째는 data 생성함수입니다. 이는 아래에 나열될 것입니다. 둘째는 visualize 함수입니다. 2D 와 3D scatter plot 을 반복적으로 그릴 것이며, 입력될 데이터의 형식은 X 와 label 이기 때문에 각 label 마다 다른 색을 칠할 기능들을 미리 작성해 두었습니다. 이는 Plotly 를 이용하여 구현하였습니다.
from soydata.data import *
from soydata.visualize import ipython_2d_scatter
from soydata.visualize import ipython_3d_scatter현재는 jupyter notebook 에서 출력 가능한 함수만을 구현했습니다. 그림을 파일로 곧바로 저장하는 함수는 며칠안에 (오늘은 2018-04-27) 구현할 예정입니다.
Two moon
두 개의 눈썹달이 서로에게 닿을듯한 모양인 데이터입니다.
x, y 축의 비율을 다르게 하여 그림을 누르거나 위아래로 늘릴 수 있습니다. xy_ratio 를 조절하여 x range, y range 의 비율을 조절합니다.
x_gap 은 0 보다 작을수록 서로의 방향으로 가까워집니다. trace 0 은 오른쪽으로, trace 1 은 왼쪽으로 이동합니다. -0.2 만큼 이동하였기 때문에 두 달이 하나로 합쳐지려 합니다.
y_gap 을 늘리면 y 축에서의 서로의 거리가 멀어집니다.
noise 는 Gaussian distribution 의 standard deviation 으로, 값을 키울수록 달의 두깨가 두꺼워집니다.
X, color = make_moons(n_samples=300,
xy_ratio=2.0, x_gap=-.2, y_gap=0.2, noise=0.1)
ipython_2d_scatter(X, color)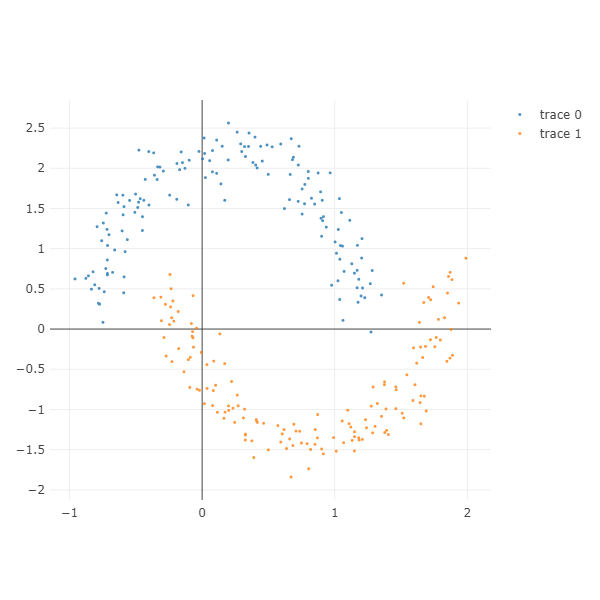
Spiral
나선형 데이터를 그릴 수 있습니다. n_classes 만큼의 나선이 만들어집니다. 각 class 마다의 샘플의 개수는 n_samples_per_class 로 설정합니다.
n_rotations 는 나선의 회전 숫자입니다.
gap_between_spiral 을 키울수록 나선 간의 간격이 멀어집니다. noise 를 키울수록 나선의 두깨가 두꺼워 집니다. 이 둘을 잘 조절하면 닿을듯 말듯 한 spirals 을 만들 수 있습니다.
gap_between_start_point=0 으로 설정하면 spirals 의 시작점이 연결되어 있습니다. 이 값을 키우면 원점에서 gap_between_start_point 만큼 떨어져 나선이 시작됩니다.
equal_interval=True 이기 때문에 나선의 바깥쪽과 안쪽의 밀도가 유지됩니다. gap_between_start_point=False 로 설정하면 나선의 중앙쪽에 샘플이 밀집되고 바깥쪽일수록 밀도가 옅어집니다.
X, color = make_spiral(n_samples_per_class=500, n_classes=3,
n_rotations=3, gap_between_spiral=0.1,
gap_between_start_point=0.1, equal_interval=True,
noise=0.2)
ipython_2d_scatter(X, color)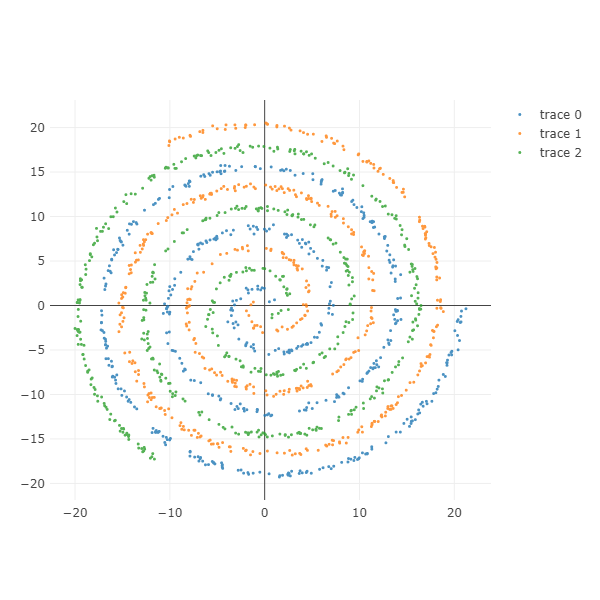
Swiss roll
복잡한 모양의 swiss roll 을 만들 수 있습니다. n_rotations 바퀴 만큼 롤이 말립니다.
gap 을 키울수록 롤 plane 간의 간격이 멀어집니다.
thickness 는 롤 plane 의 두깨입니다. thickness 를 키울수록 롤 plane 의 두깨가 두꺼워집니다.
width 는 y 축의 range 입니다. y 를 키우면 옆으로 긴 롤케잌을 만들 수 있습니다.
X, color = make_swiss_roll(n_samples=3000, n_rotations=3,
gap=0.5, thickness=0.0, width=10.0)
ipython_3d_scatter(X, color)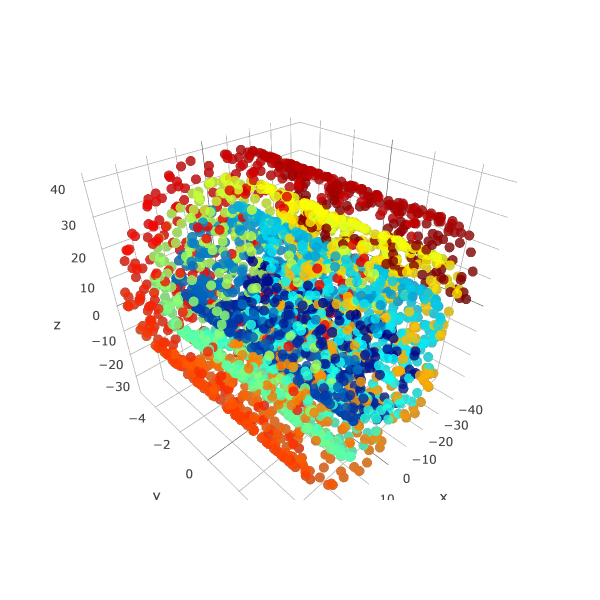
Radial
방사형 데이터를 만들 수 있습니다. n_classes 만큼의 클래스가 서로 반복되어 만들어집니다.
n_classes \(\times\) n_sections_per_class 만큼의 sections 이 만들어집니다. 아래는 6 개의 sections 이 만들어졌습니다.
각 section 의 samples 개수는 n_samples_per_sections 로 조절합니다. 아래는 총 600 개의 점이 그려져 있습니다.
gap 을 늘리면 각 section 간의 간격이 멀어집니다. gap 은 [0, 1] 사이의 값입니다.
equal_proportion=True 이면 각 section 의 원점에서의 각도 기준 영역이 같습니다. equal_proportion=False 이면 section 마다 각도가 random 으로 만들어집니다. 하지만 한 바퀴를 n_classes \(\times\) n_sections_per_class 등분함은 유지됩니다.
radius_min 은 모든 samples 의 최소 radius 입니다. radius_min=0 으로 설정하면 원점 근처에 샘플이 만들어질 수 있습니다.
radius_base 는 각 section 의 평균 radius 입니다.
여기에 radius_variance > 0 으로 설정하면 평균 radius 에 편차가 발생합니다.
X, color = make_radial(n_samples_per_sections=100, n_classes=2,
n_sections_per_class=3, gap=0.1, equal_proportion=True,
radius_min=0.1, radius_base=1.0, radius_variance=0.5)
ipython_2d_scatter(X, color)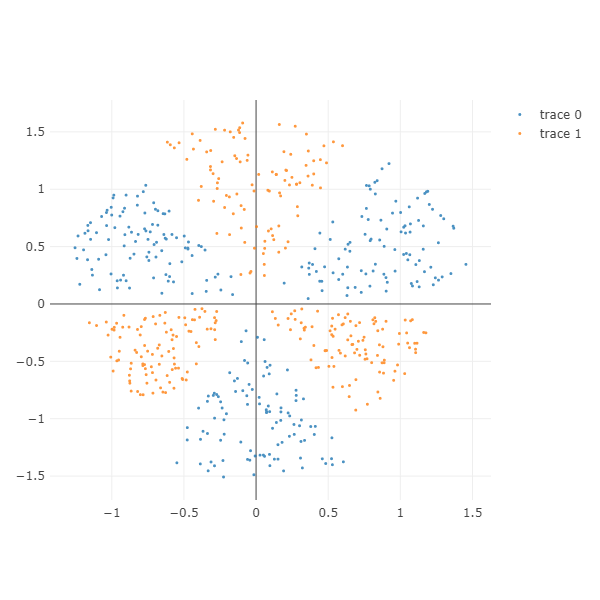
Two layers radial
Radial data 를 만드는 함수를 이용하여 two layer radial data 를 만들 수 있습니다. Parameters 는 동일합니다.
One layer radial data 는 one hidden layer feed-forward neural network 로 분류가 가능합니다. 하지만 Two layers radial data 는 적어도 두 개 이상의 hidden layers 가 필요합니다. 이를 확인하기 위한 데이터입니다.
X, color = make_two_layer_radial(n_samples_per_sections=100, n_classes=2,
n_sections_per_class=3, gap=0.0, equal_proportion=False)
ipython_2d_scatter(X, color)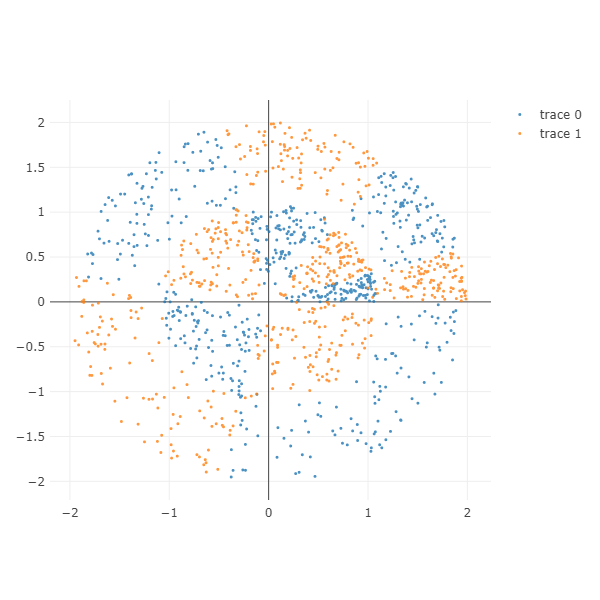
Rectangular
사각형을 만드는 함수입니다. x_b, x_e, y_b, y_e 는 사각형의 좌측 하단의 좌표 (x_b, y_b) 와 사각형의 우측 상단의 좌표 (x_e, y_e) 값입니다.
X, color = make_rectangular(n_samples=500,
label=0, x_b=0, x_e=10, y_b=0, y_e=10)
ipython_2d_scatter(X, color)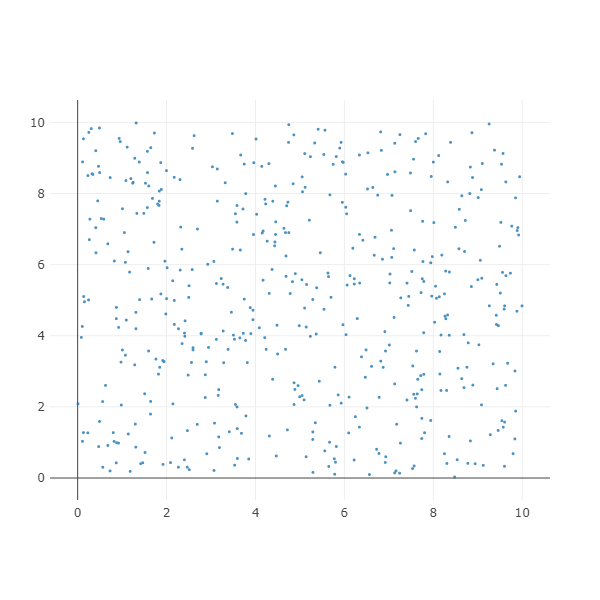
Triangular
삼각형을 만들 수 있습니다. Upper triangular 를 만들기 위해서 upper=True 로 설정합니다. 다른 parameters 는 make_rectangular() 와 같습니다.
X, color = make_triangular(n_samples=500, upper=True,
label=0, x_b=0, x_e=10, y_b=0, y_e=10)
ipython_2d_scatter(X, color)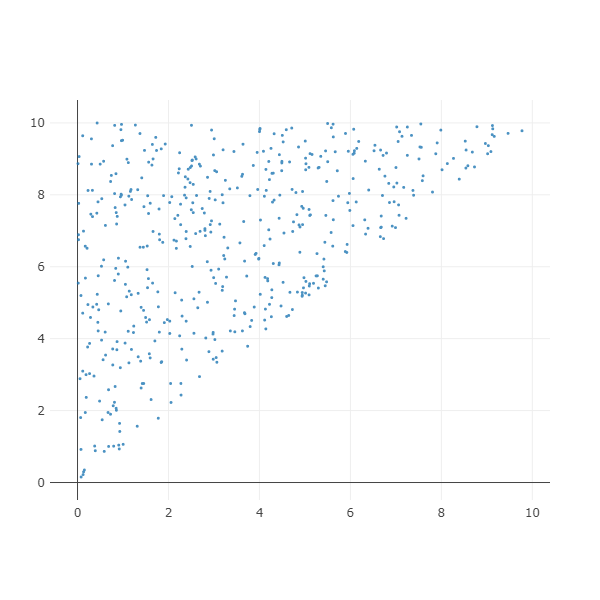
Lower triangular 를 만드려면 upper=False 로 설정합니다.
X, color = make_triangular(n_samples=500, upper=False,
label=0, x_b=0, x_e=10, y_b=0, y_e=10)
ipython_2d_scatter(X, color)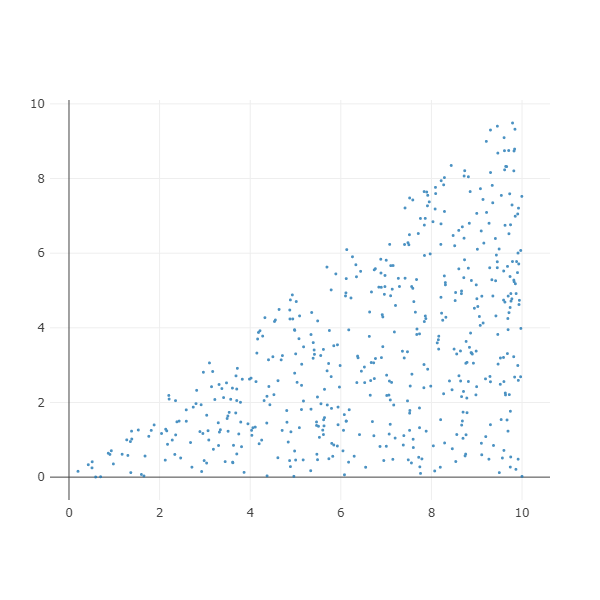
Decision Tree dataset 1
삼각형과 사각형을 만드는 함수를 이용하면 아래와 같은 복잡한 형태의 데이터셋을 만들 수 있습니다.
Decision tree dataset 은 구조를 미리 정의한 데이터셋입니다. 이 구조에 맞춰 n_samples 개수 만큼의 samples 를 만듭니다.
Decision tree dataset 1 은 사각형만으로 이뤄진 데이터이기 때문에 하나의 decision tree 만으로도 classification 을 잘 수행할 수 있습니다.
X, color = get_decision_tree_data_1(n_samples=2000)
ipython_2d_scatter(X, color)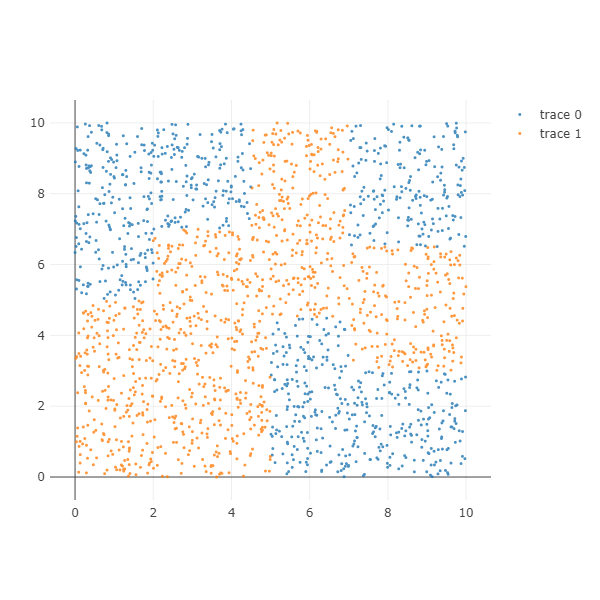
Decision Tree dataset 2
Decision tree dataset 2 은 삼각형이 포함되어 있습니다. 한 번에 하나의 변수를 이용하여 branch 하는 단일 decision tree 를 이용한다면 많은 depth 가 필요합니다.
X, color = get_decision_tree_data_2(n_samples=2000)
ipython_2d_scatter(X, color)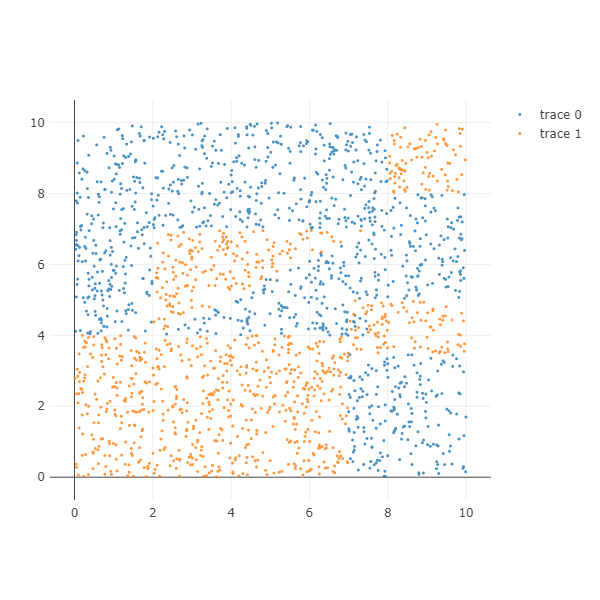
Creating your decision tree dataset
Decision tree dataset 2 은 make_rectangular() 와 make_triangular() 를 이용하여 만들었습니다.
profile 은 각 구성요소의 (type, n sample ratio, label, x_b, x_e, y_b, y_e) 로 구성된 길이가 7 인 tuple 의 list 입니다.
profile = [
('rec', 32, 1, 0, 7, 0, 4),
('rec', 9.5, 0, 7, 10, 0, 3.5),
('rec', 4.5, 1, 7, 10, 3.5, 5),
('rec', 0.5, 1, 7.5, 8, 4, 5),
('rec', 7.5, 0, 7.5, 10, 5, 8),
('rec', 4.5, 1, 8, 10, 8, 10),
('rec', 1, 0, 7.5, 8, 8, 10),
('rec', 16.5, 0, 2, 7.5, 7, 10),
('rec', 12, 0, 0, 2, 4, 10),
('upper', 8.25, 1, 2, 7.5, 4, 7),
('lower', 8.25, 0, 2, 7.5, 4, 7),
]Tuple 의 2 번째 값은 samples 개수의 비율입니다. 전체 1000 개의 samples 을 만드려면 다음처럼 한 구성요소에 sample number ratio 의 몇 배 만큼의 samples 을 만들어야 하는지를 미리 계산해야 합니다.
factor = n_samples / sum((p[1] for p in profile))type 이 ‘rec’ 이면 rectangular 를, ‘upper’ 나 ‘lower’ 이면 각각에 맞는 삼각형을 만듭니다.
numpy.concatenate 에 list of numpy.ndarray 를 입력하면 row 기준으로 행렬을 이어줍니다. column 기준으로 행렬을 이으려면 axis=1 로 설정하면 됩니다.
데이터의 모양을 profile 로 만들어 둔 뒤, 아래 함수를 이용하여 다양한 decision tree dataset 을 만듭니다.
import numpy as np
def _get_decision_tree_data(profile, n_samples=1000):
# set num of samples
factor = n_samples / sum((p[1] for p in profile))
X_array = []
color_array = []
for i, p in enumerate(profile):
n_samples_ = int(p[1] * factor)
#label = i
label = p[2]
if p[0] == 'rec':
X, color = make_rectangular(n_samples_,
label=label, x_b=p[3], x_e=p[4], y_b=p[5], y_e=p[6])
elif p[0] == 'upper':
X, color = make_triangular(n_samples_, True,
label=label, x_b=p[3], x_e=p[4], y_b=p[5], y_e=p[6])
elif p[0] == 'lower':
X, color = make_triangular(n_samples_, False,
label=label, x_b=p[3], x_e=p[4], y_b=p[5], y_e=p[6])
else:
raise ValueError('Profile type error. Type={}'.format(p[0]))
X_array.append(X)
color_array.append(color)
X = np.concatenate(X_array)
color = np.concatenate(color_array)
return X, color