의사결정나무 (Decision tree) 는 classification 과정에 대한 해석을 제공하는 점과 다른 classifiers 보다 데이터의 전처리를 (상대적으로) 덜해도 된다는 장점이 있습니다. 하지만 bag of words model 과 같은 sparse data 의 분류에는 적합하지 않습니다. 이번 포스트에서는 의사결정나무가 무엇을 학습하는지 알아보고, 왜 sparse data 에는 적합하지 않은지에 대하여 이야기합니다.
Decision trees
의사결정나무는 데이터의 공간을 직사각형으로 나눠가며 최대한 같은 종류의 데이터로 이뤄진 부분공간을 찾아가는 classifiers 입니다. 마치 clustering 처럼 비슷한 공간을 하나의 leaf node 로 나눠갑니다. 아래의 데이터를 분류하는 decision tree 를 학습한다고 가정합니다.
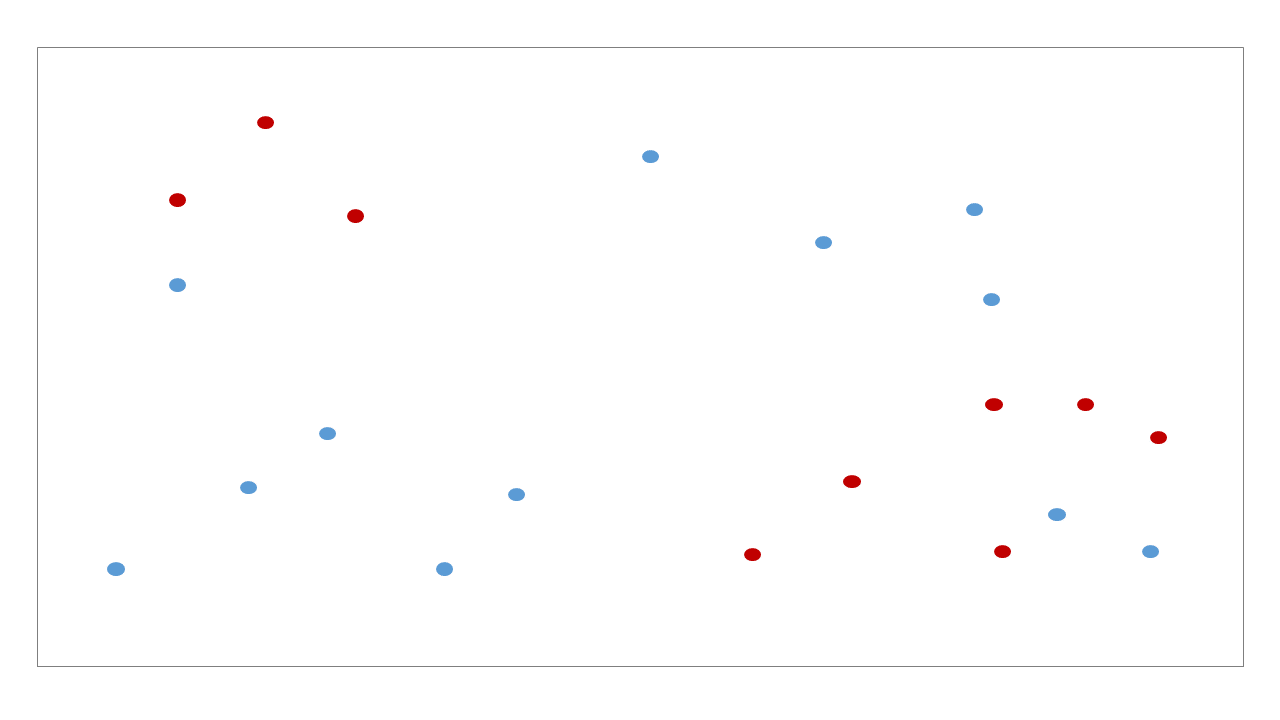
Decision tree 는 매번 각 변수에서 적절한 기준선을 찾아가며 공간을 이분 (bisect)합니다. 이 과정을 조건이 만족할 때까지 반복합니다.
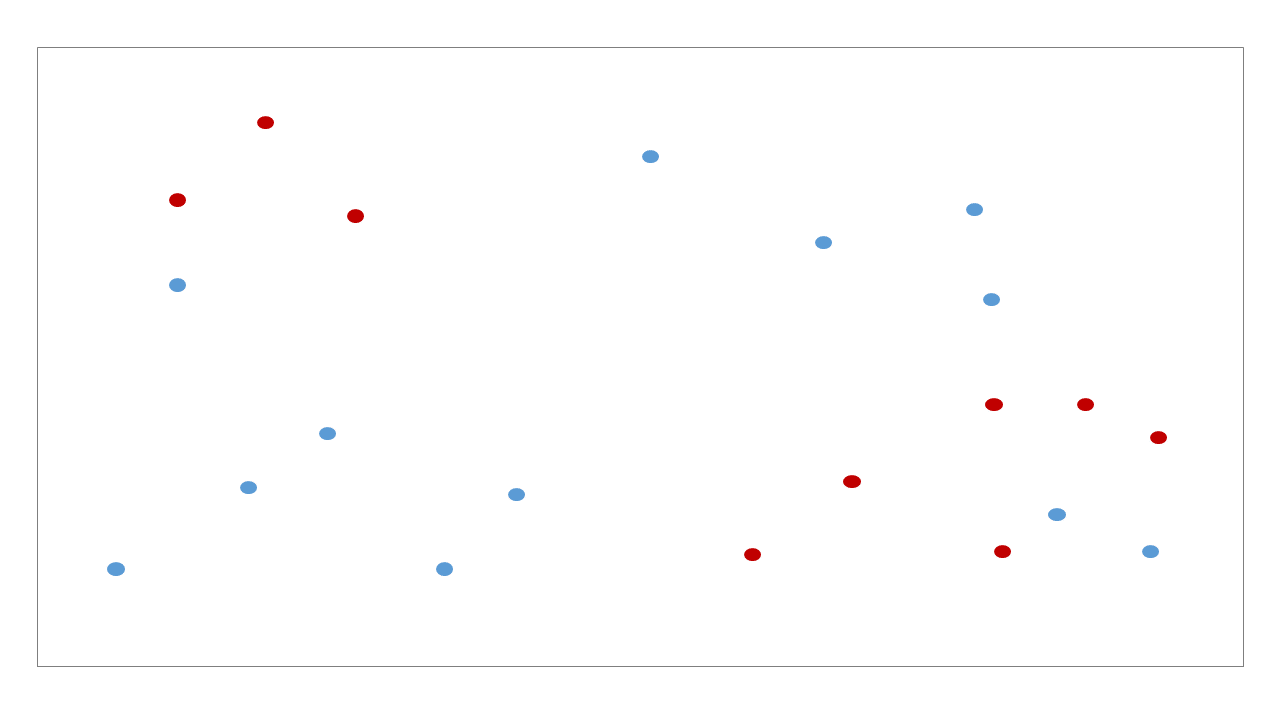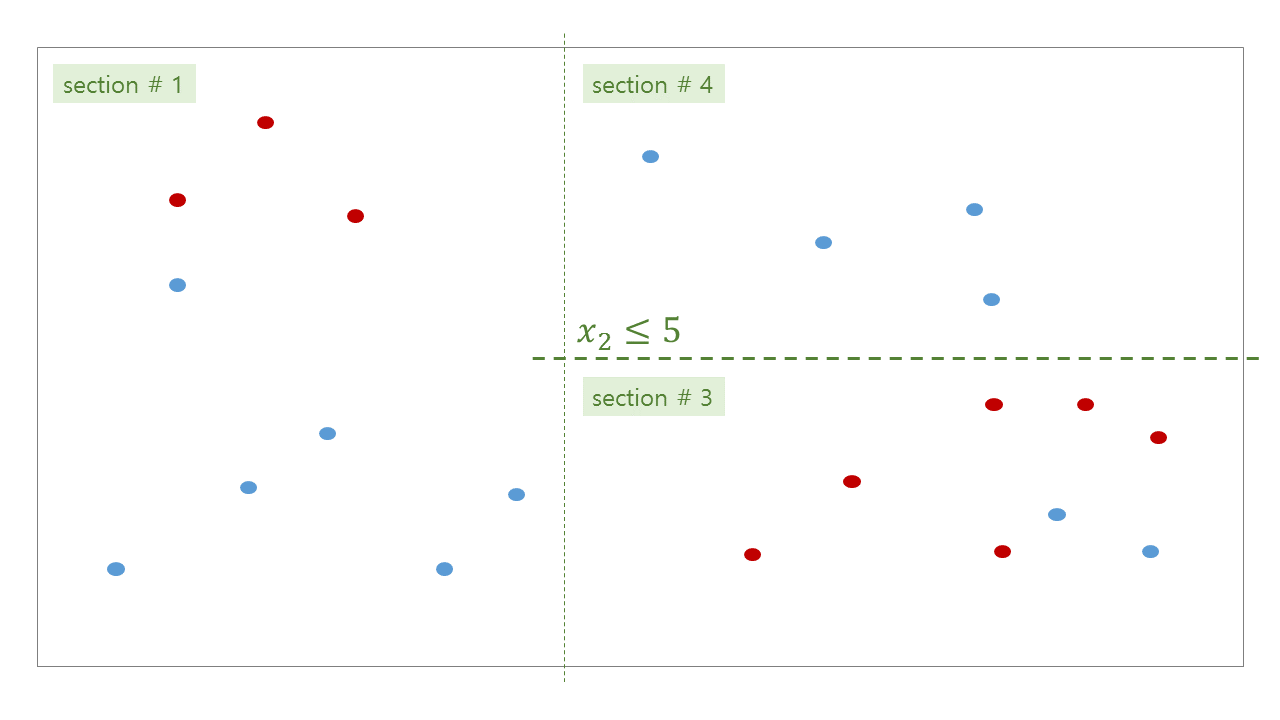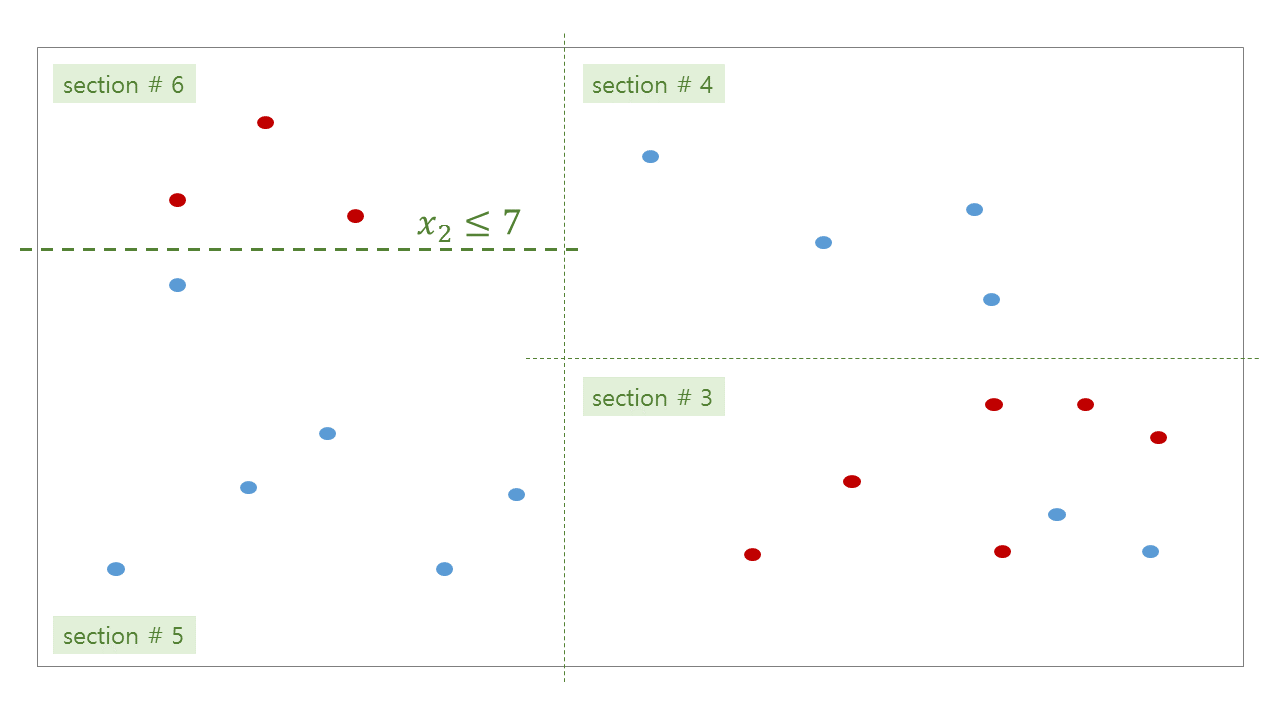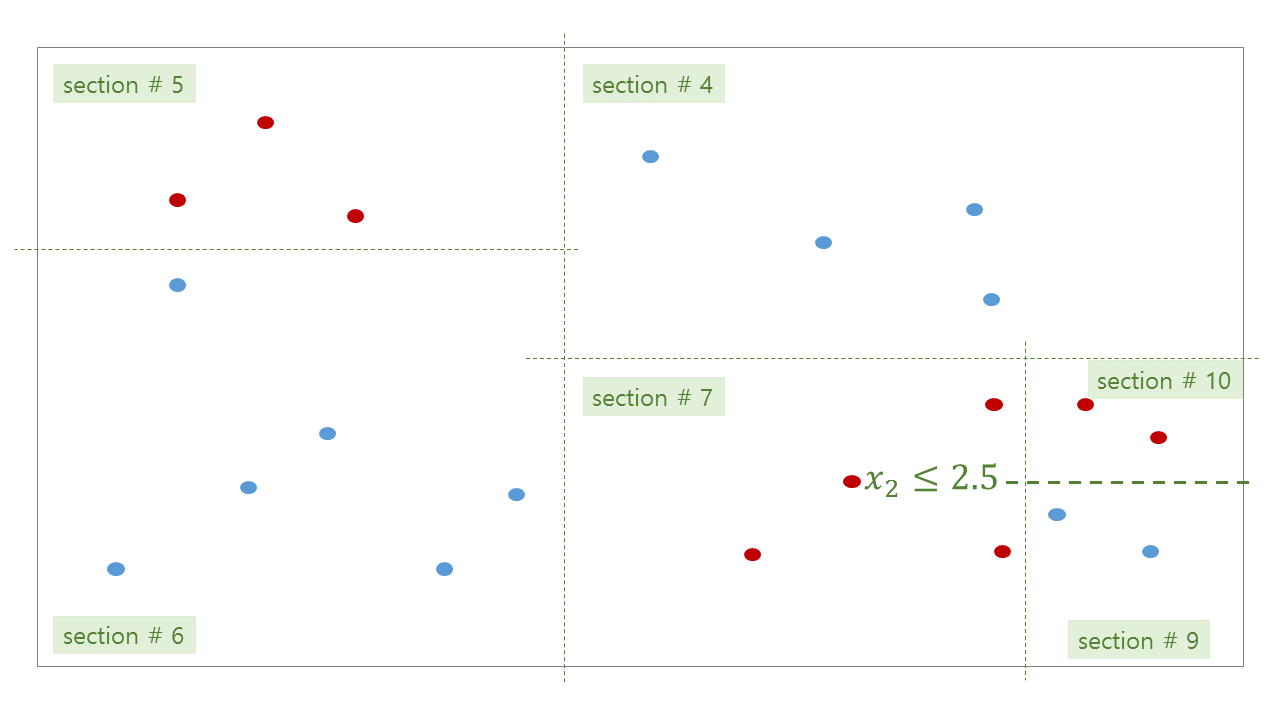
조건이란, 내가 만족할만한 purity 를 얻거나 (한 노드에 빨간색 9, 파란색 1 이 있다면 purity 는 0.9 입니다), 내가 제한하는 최대 깊이 (depth) 까지 공간을 분할하였거나, 직사각형에 포함된 점의 개수등이 최소 개 이상이 될 때 까지 입니다. 이 조건들은 decision tree 학습 시 사용자가 지정하는 parameters 입니다.
위 그림처럼 tree 가 학습된 뒤, 우리는 각 공간에 대한 bisection path 를 얻을 수 있습니다. #0 공간인 root 는 #1 과 #2 로 나눠지고, #2 는 #3 과 #4 로 나눠집니다. 이 모습이 마치 나무같기에 decision tree 라 부릅니다.
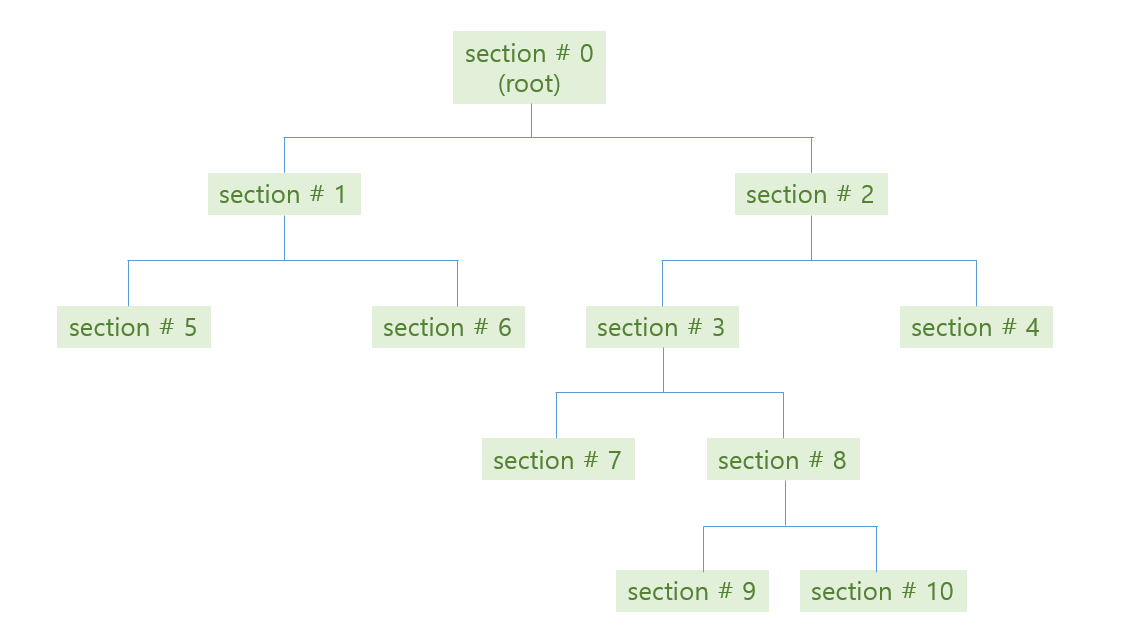
Tree 의 각 section 을 마디 (node) 라 부릅니다. 그 중, #4, #5, #6, #7, #9, #10 처럼 더 이상 자라나지 않는 마지막 마디를 leaf nodes, leaves 라 합니다. 줄기가 아닌 나무의 끝부분이라는 뜻입니다. Branching 은 #3 이 #7 과 #8 로 나뉘어짐을 표현합니다. 이처럼 depth 가 깊어지는 과정을 나무가 자라난다라고 표현하기도 합니다. #7 과 #8 은 #3 에서 자라났기 때문에 children 이라 부르며, #3 은 #7 과 #8 의 parent 입니다.
각 branching 단계마다 decision rule 이 정해집니다. Decision rule 은 사용할 변수와 threshold 로 이뤄집니다. 예를 들어 #0 -> (#1, #2) 으로 나눠지는 기준은 입니다. 이 4 보다 작으면 section #1 로, 4 보다 크면 section #2 로 판단됩니다. 위 그림의 path 를 따라 leaf node 에 도달할 때까지 계속하여 rule classifications 을 수행합니다. 한 query 에 대한 최대 classifications 횟수는 최대 depth 입니다.
| section no | # red | # blue | # entropy | # decision | # left child | # right child |
|---|---|---|---|---|---|---|
| 0 | 9 | 12 | 0.297 | 1 | 2 | |
| 1 | 3 | 6 | 0.276 | 5 | 6 | |
| 2 | 6 | 6 | 0.301 | 3 | 4 | |
| 3 | 6 | 2 | 0.244 | 7 | 8 | |
| 4 | 0 | 4 | 0 | - | - | - |
| 5 | 3 | 0 | 0 | - | - | - |
| 6 | 0 | 6 | 0 | - | - | - |
| 7 | 4 | 0 | 0 | - | - | - |
| 8 | 2 | 2 | 0.301 | 9 | 10 | |
| 9 | 0 | 2 | 0 | - | - | - |
| 10 | 2 | 0 | 0 | - | - | - |
예시는 두 개의 변수를 이용하지만, 변수가 100 개이고 최대 depth 가 5 정도라면 이용하지 않는 변수들도 존재합니다. Decision tree 는 classification 과정에 유용한 변수만을 선택하여 이용한다는 측면도 있습니다.
Branching 을 할 수 있는 점은 다양합니다. 그 중, 공간을 2 개로 나눴을 때 평균 entropy 가 가장 크게 감소하는 방향으로 branching 을 합니다. 이를 Information gain 이라 합니다. 아래처럼 기술됩니다. 특정 분기를 하였을 때 분기하기 전보다 purity 를 높이는 방향으로 분기합니다.
Decision tree 는 한 변수가 어떤 의미를 지닐 때 이용할 수 있는 알고리즘입니다. 그렇기 때문에 Doc2Vec 과 같이 embedding algorithm 을 이용하여 distributed representation 으로 표현된 데이터의 분류에는 적합하지 않습니다. 차원에 특정한 의미가 없기 때문입니다.
또한 몇 개의 변수들을 독립적으로 이용해도 분류가 잘 될 수 있는 데이터에 적합합니다. Leaves 는 rectangular 모양의 공간 입니다. 이 공간 안에서는 대체로 비슷한 labels 을 지닐 것이라 가정합니다. 여러 변수가 서로 상관성이 높을 경우에는 잘 작동하지 않습니다.
Decision tree 도 logistic regression 처럼 regularization 을 할 수 있습니다. 다양한 방법들이 있지만, configuration 을 이용할 수 있습니다. Regularization 의 목적은 trade off 관계인 성능과 모델복잡도의 중요도를 조절하여 좋은 분류 성능을 보이면서도 간단한 모델을 만들기 위함입니다.
Decision trees in scikit learn
Scikit learn 에서는 decision tree 를 제공합니다. 앞서 언급하였던 regularization 을 위한 user configuration parameters 를 입력할 수 있습니다.
from sklearn.tree import DecisionTreeClassifier
decision_tree = DecisionTreeClassifier(
max_depth=10,
min_samples_split=2,
min_samples_leaf=5,
max_features=None,
max_leaf_nodes=None,
class_weight=None
)
decision_tree.fit(X, y)학습된 tree 가 이용하는 features 들과 각 features 의 상대적 중요도를 얻을 수 있습니다. 이는 feature_importances_ 에 저장되어 있습니다. 이를 살펴보면 가장 중요한 features 들이 무엇인지, 그리고 tree 가 이용하는 featues 의 개수가 몇 개인지도 확인할 수 있습니다. feature_importances_ 는 x.shape[1] 크기의 array 입니다. 각 features 에 대한 상대적 중요도가 저장되어 있습니다.
print(decision_tree.feature_importances_.shape)
# (2770,)
print(decision_tree.feature_importances_.sum())
# 1.0이 중에서 상대적 중요도가 0 보다 큰 features 만을 선택할 수 있습니다. Decision tree 가 이용하는 features 입니다.
import numpy as np
np.where(decision_tree.feature_importances_ > 0)[0]sorted 를 이용하여 가장 중요한 topk 개의 features 를 살펴볼 수 있습니다.
sorted(
filter(lambda x:x[1]>0,
enumerate(decision_tree.feature_importances_)),
key=lambda x:-x[1]
)Decision tree for text classification
Document classification 의 경우, 하나의 document 를 bag of words model 과 같은 sparse vector 나 Doc2Vec 과 같은 distributed representation 으로 표현한 뒤, classifiers 를 학습합니다.
Decision tree 가 잘 작동할 수 있는 조건은 (1) 공간의 각 차원에 특별한 의미가 있으며, (2) 각 변수들을 독립적으로 이용하여도 분류를 할 수 있는 데이터 입니다. 그렇기 때문에 각 차원에 특별한 의미를 지니지 않는 distributed representation 은 decision tree 에 맞지 않습니다.
Term frequency vector 나 tf-idf vector 로 문서를 표현할 경우에도 decision tree 는 좋지 않습니다. Decision tree 의 장점 중 하나는 몇 개의 변수를 선택적으로 이용하는 것입니다. Bag of words model 의 경우에는 몇 개의 단어를 선택한다는 의미가 됩니다. 문서 분류가 잘 되려면 tree 가 선택한 단어들을 데이터의 모든 문서들이 가지고 있어야 합니다. -은, -는, -이, -가 처럼 문법 기능을 하지 않는 단어들을 제외하고, 감성분석에서의 ‘좋다’, ‘재미있다’ 와 같은 단어를 많은 문서들이 가지고 있기는 어렵습니다. 결국은 많은 문서들을 cover 하려면 많은 단어를 이용합니다. 특히 뉴스처럼 여러 단락으로 이뤄진 문서가 아니라, 영화평과 같이 짧은 문서일수록 decision tree 에게는 힘든 데이터입니다.
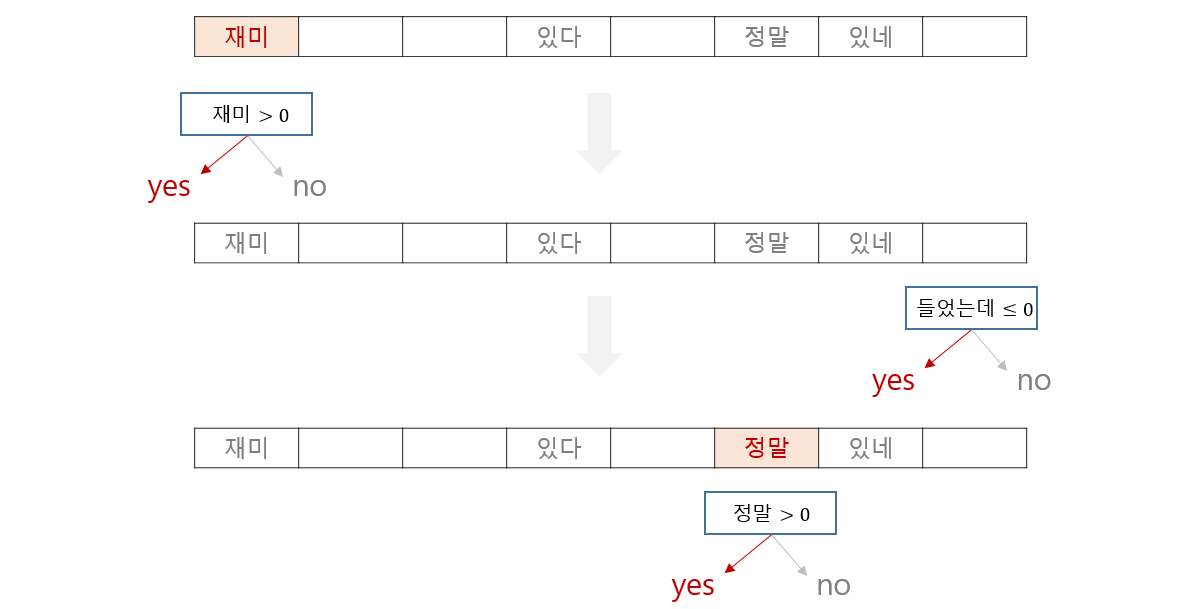
그 과정에서 한 단어씩 따로따로 살펴봅니다. 복잡하지 않은 난이도의 document classifications 은 특정 단어가 문서에 등장하였느냐가 중요한 힌트입니다. Logistic regression 처럼 한 번에 살펴볼 수 있는 문제를 굳이 tree path 를 따라 classification 할 필요는 없습니다.
이를 확인하기 위하여 영화 평점 데이터를 이용한 sentiment classification 을 수행하였습니다. 영화평의 감성 분석을 위해서는 데이터 전처리가 필요합니다. 영화 평점은 1 ~ 10 점을 지닙니다. 사람마다 점수의 기준이 다르기 때문에 4 ~ 7 점은 긍/부정을 명확히 판단하기 어려워 제외하였습니다. 또한 1 ~ 3 점을 서로 다른 클래스로 구분하는 것도 큰 의미가 없습니다. 그렇기 때문에 1 ~ 3 점은 negative, 8 ~ 10 점은 positive 로 레이블을 부여하였습니다.
13,817 개의 단어로 이뤄진 242k 개의 문장입니다.
print(x.shape)
# (242718, 13817)일반화 성능을 검증하기 위하여 cross validation 을 이용하였습니다. scikit-learn 에서는 cross validaton 과정을 함수로 제공합니다. Decision tree 처럼 features 를 선택하는 능력을 지닌 lasso regression 과 함께 cross validation 성능을 비교하였습니다.
둘 모두 이용하는 features 의 개수를 확인하기 위하여 모든 데이터를 이용하는 학습도 마지막에 거쳤습니다.
from sklearn.tree import DecisionTreeClassifier
from sklearn.cross_validation import cross_val_score
n_cv = 10
for depth in [10, 20, 30, 50]:
# ready for decision tree
decision_tree = DecisionTreeClassifier(
max_features=None,
max_depth=depth
)
# cross validation
scores = cross_val_score(
decision_tree, x, y, cv=n_cv)
average_score = sum(scores) / n_cv
# check number of used features
decision_tree.fit(x,y)
useful_features = list(
filter(lambda x:x[1]>0,
enumerate(decision_tree.feature_importances_)
)
)
n_useful_features = len(useful_features)
print('depth = {}, cross-validation average = {:.4}, n useful featuers = {}'.format(
depth, average_score, n_useful_features))더 많은 features 를 이용할 수 있도록 max_depth 만 조절하고 다른 parameters 는 고정였습니다. Depth 가 10 일 때 141 개의 단어를 이용하여 76.65 % 의 정확도를 보입니다. 그러나 depth 가 50 이 되어도 성능의 향상은 그리 크지 않습니다. 하지만 사용한 featuers 의 개수는 2k 가 넘습니다. 15 % 의 단어를 이용하거나 1% 의 단어를 이용하거나 성능은 비슷합니다.
depth = 10, cross-validation average = 0.7665, n useful featuers = 141
depth = 20, cross-validation average = 0.7804, n useful featuers = 588
depth = 30, cross-validation average = 0.7886, n useful featuers = 1128
depth = 50, cross-validation average = 0.7969, n useful featuers = 2022
Lasso penalty 를 이용하여 logistic regression 을 학습합니다. Regularization cost 인 C 만 조절하였습니다.
from sklearn.linear_model import LogisticRegression
for cost in [100, 10, 1, 0.1, 0.01]:
logistic_regression = LogisticRegression(
penalty='l1', C=cost)
scores = cross_val_score(
logistic_regression, x, y, cv=n_cv)
average_score = sum(scores) / n_cv
logistic_regression.fit(x,y)
useful_features = list(
filter(lambda x:x[1]>0,
enumerate(logistic_regression.coef_[0])
)
)
n_useful_features = len(useful_features)
print('L1 lambda = {}, cross-validation = {}, n useful features = {}'.format(
1/cost, average_score, n_useful_features))대체로 decision tree 보다 좋은 성능을 보입니다.
일 때는 regularization 의 효과가 거의 없기 때문에 대부분의 단어를 분류에 이용합니다. 이때는 85.24 % 의 정확도를 보입니다. 하지만 일 때에는 932 개의 단어만을 이용하고도 85.00 % 의 정확도를 보입니다. 7 % 의 단어를 이용하고도 85 % 의 성능을 보입니다. 그러나 decision tree 는 15 % 의 단어를 이용하고도 79.69 % 의 정확도를 보입니다. Recursive 한 방식으로 단어의 유무를 살펴본 것이 오히려 독이 되었습니다.
L1 lambda = 0.01, cross-validation = 0.8523798115500554, n useful features = 7263
L1 lambda = 0.1, cross-validation = 0.8562237871803605, n useful features = 6897
L1 lambda = 1.0, cross-validation = 0.8646945561762077, n useful features = 4226
L1 lambda = 10.0, cross-validation = 0.8499696571854498, n useful features = 932
L1 lambda = 100.0, cross-validation = 0.8060669125960622, n useful features = 177
또한 의사결정나무는 threshold 를 이용합니다. 모든 단어가 1 번 나오고, 한 문장이 네 개의 단어로만 구성되어 있다면 L2 normalization 을 한 term frequency vector 에서의 각 단어의 weight 는 1/2 입니다. 그러나 아홉 개의 단어로 구성된 문장에서의 각 단어의 weight 는 1/3 입니다. 만약 decision rules 의 threshold 가 0.4 로 설정된다면 1/3 의 weight 를 지니는 문장은 해당 단어를 포함했음에도 불구하고, 상대적으로 문서가 길다는 이유로 잘못 분류될 수 있습니다.
Document classification 에서는, 특히 짧은 문서에서는 특정 단어가 등장하였느냐의 유무가 중요합니다. 이런 측면에서 decision tree 는 document classification 에 적합하지 않습니다. 그리고 bag of words model 처럼 sparse vector 로 표현되는 데이터에서는 threshold 와 같은 값에 민감할 수 있기 때문에 decision tree classifier 를 지양하라는 기존 연구들도 많이 있습니다.