L1 regularity 는 분류/예측 성능은 유지하면서 모델의 coefficients 를 최대한 sparse 하게 만듭니다. PyTorch 를 이용하여 L1 regularity 를 부여하는 방법을 살펴봅니다. 이는 custom cost function 을 구현하는 내용이기도 합니다.
L1 Regularity & Lasso Regression
L1 regularity 는 분류/예측 성능은 유지하면서 모델의 coefficients 를 최대한 sparse 하게 만듭니다. Sparse models 은 해석력이 있을 뿐더러, 실제 이용하는 parameters 의 숫자가 줄어들어 모델의 압축에도 유용합니다. L1 regularity 를 이용하는 Softmax Regression 을 Lasso Regression 이라고도 하며, 이전의 블로그 에서 Lasso Regression 을 이용하여 키워드를 추출하는 법도 다뤘습니다. 그 외에도 Sparse Coding 은 sparse vector representation 을 학습하는 방법으로, semantic 한 정보를 보존하면서도 해석력이 있는 sparse vector 를 학습하기도 합니다.
scikit learn 의 많은 모델들이 L1 regularity 를 제공합니다. 대표적으로 Logistic Regression 과 Nonnegative Matrix Factorization (NMF) 는 간단한 argument 설정으로 L1 regularity 를 부여할 수 있습니다. Logistic Regression 에서 penalty 를 l1 으로 설정하면 아래의 비용 함수를 최소화 하는 solutions 을 계산합니다. cost 는 모델이 얼마나 분류를 잘하느냐의 loss 와 모델의 L1 norm 으로 정의되는 regularity 를 더한 형태로 정의됩니다. 아래 식의 의미는 분류를 잘하면서도 \(\theta\) 는 sparse 하게 학습하라는 것입니다.
from sklearn.linear_model import LogisticRegression
logistic_l1 = LR(penalty='l1', C=1.0)
logistic_l1.fit(x, y_true)Nonnegative Matrix Factorization 은 데이터 \(X\) 를 representation \(W\) 와 dictionary \(H\) 로 분해하되, \(W, H\) 의 components 가 모두 non-negative 하게 만드는 factorization 방법입니다. 이 때에도 L1 regularity 를 적용할 수 있습니다. Scikit-learn 의 NMF 는 아래의 비용 함수를 최소화 합니다. l1_ratio \(=\gamma\) 를 1 로 설정하면 L1 regularity 만을 적용합니다.
from sklearn.decomposition import NMF
nmf = NMF(n_components=200, l1_ratio=1.0)
z = nmf.fit_transform(x)우리는 Lasso Regression 의 성능을 확인하기 위하여 아래와 같은 인공데이터를 만들어 실험을 해봅니다.
import numpy as np
n_data = 1000
n_features = 3000
noise = 0.01
probs = np.linspace(0.1, 0.005, num=n_features)
def fill(prob):
if np.random.random() >= prob:
return 0
return np.random.randint(1, 2)
def make_sparse_data(n_data, n_features, probs):
x = np.zeros((2 * n_data, 2 * n_features))
y = np.asarray([0] * n_data + [1] * n_data)
for i in range(n_data):
for j in range(n_features):
x[i,j] = fill(probs[j])
x[i,j + n_features] = fill(max(probs[j] * 10 * noise, noise))
x[i+n_data,j+n_features] = fill(probs[j])
x[i+n_data,j] = fill(max(probs[j] * 10 * noise, noise))
return x, y
x, y_true = make_sparse_data(n_data, n_features, probs)가운데를 중심으로 위쪽은 0, 아래쪽은 1 의 y 를 지니는 binary classifation 용 sparse data 입니다.
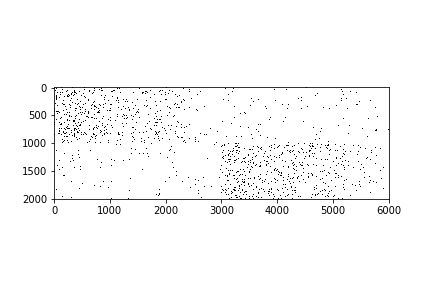
L2 regularity 를 이용하는 Logistic Regression 을 이용하면 정확히 분류가 가능한 데이터입니다.
from sklearn.linear_model import LogisticRegression as LR
logistic_l2 = LR()
logistic_l2.fit(x, y_true)
y_pred = logistic_l2.predict(x)
def accuracy(y_true, y_pred):
return np.where(y_true == y_pred)[0].shape[0] / y_true.shape[0]
accuracy(y_true, y_pred) # 1.0L1 regularity 를 이용하는 Lasso Regression 을 이용하여도 분류가 가능합니다. Regularity cost 에 따라서 nonzero coefficient 를 지니는 변수의 개수도 확인합니다.
from sklearn.linear_model import LogisticRegression
for c in [100, 10, 5, 2, 1, 0.5, 0.2, 0.1, 0.07, 0.03, 0.01]:
logistic_l1 = LR(penalty='l1', C=c)
logistic_l1.fit(x, y_true)
y_pred = logistic_l1.predict(x)
train_accuracy = accuracy(y_true, y_pred)
nnz = np.where(abs(logistic_l1.coef_[0]) > 0)[0].shape[0]
print('c = {}, accuracy = {}, nnz = {}'.format(c, train_accuracy, nnz))강한 regularity 를 부여할수록 nonzero elements 의 개수가 줄어듦을 알 수 있습니다. C = 0.07 으로 설정한 경우에는 3000 개의 변수 중 331 개의 변수만을 이용하여 정확하게 분류를 하는 Lasso Regression 도 학습합니다.
c = 100, accuracy = 1.0, nnz = 1370
c = 10, accuracy = 1.0, nnz = 817
c = 5, accuracy = 1.0, nnz = 738
c = 2, accuracy = 1.0, nnz = 662
c = 1, accuracy = 1.0, nnz = 632
c = 0.5, accuracy = 1.0, nnz = 563
c = 0.2, accuracy = 1.0, nnz = 481
c = 0.1, accuracy = 1.0, nnz = 395
c = 0.07, accuracy = 1.0, nnz = 331
c = 0.03, accuracy = 0.9955, nnz = 143
c = 0.01, accuracy = 0.5, nnz = 0
Implementing Lasso Regression using PyTorch
Lasso Regression 이 학습될 수 있는 데이터임을 확인했으니, PyTorch 를 이용하여 이를 재구현 합니다. 포스트 작성 당시의 PyTorch 의 버전은 0.4.0 입니다.
PyTorch 에서는 optimizer 에서 L2 regularity 를 부여하는 기능을 제공합니다. Optimizer 중 하나인 Adam 의 default arguments 입니다. weight_decay 가 0 으로 설정되어 있는데, 이 값이 L2 regularity coefficient \(\lambda\) 입니다. 이를 0 보다 큰 값으로 설정하면 L2 regularity 가 부여됩니다. 하지만 L1 regularity 는 따로 제공되지 않습니다.
import torch.optim as optim
optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)일단 Logistic Regression 을 만듭니다. Linear layer 하나만 이용하여 구현할 수 있습니다.
import torch.nn as nn
class LogisticRegression(nn.Module):
def __init__(self, input_dim, n_classes, bias=True):
super().__init__()
self.fc = nn.Linear(input_dim, n_classes, bias=bias)
def forward(self, X):
out = self.fc(X)
return out학습을 위한 train 함수를 구현합니다. model, loss_function, optimizer, 학습 데이터 x, y 를 입력받습니다. 반복횟수 epochs 를 설정합니다. c 는 regularity coefficient 이며, penalty 를 l2 로 설정하면 L2 regularity 를, l1 으로 설정하면 L1 regularity 를 부여하도록 합니다. CUDA 이용을 위한 use_gpu 도 추가합니다.
def train(model, loss_func, optimizer, x, y, epochs,
c=1.0, penalty='l1', sparse_threshold=0.0005, use_gpu=False):
...Classification error 에 의한 loss 는 loss_function 에 의하여 계산할 수 있습니다. 정답인 y 와 예측값인 y_pred 를 loss_func 에 입력하여 loss 를 계산합니다. Regularity 는 torch.norm 을 입력하여 계산합니다. cost 는 loss 와 regularity 의 합으로 정의합니다.
...
# predict
y_pred = model(x)
# defining cost
loss = loss_func(y_pred, y)
regularity = torch.norm(model.fc.weight, p=p)
cost = loss + c * regularity
...이 때 한 가지 주의할 점이 있습니다. Type 을 살펴보면 loss, regularty 모두 torch.Tensor 입니다. 처음에 norm 함수에 입력할 값을 Tensor 로 입력하여도 될거라 생각하여 아래와 같이 구현을 했습니다. weight 의 type 은 nn.Linear 의 Parameters 입니다. data 의 type 은 torch.Tensor 입니다. 그런데 아래처럼 Parameters 가 아닌 value 를 cost 에 입력하면 그 값이 gradient 계산에 입력되지 않습니다. 반드시 Parameters 를 입력해야 합니다.
...
regularity = torch.norm(model.fc.weight.data, p=p)
...그래서 다른 예시 코드들을 살펴보면 아래처럼 L1 regularity 를 계산하라고 합니다. Parameters 가 입력되어야 하는 줄 모르고 원인을 못찾아서 처음에 해맸었습니다. Regularity 가 cost 에 적용되지 않는다면 cost 에 입력한 값의 type 이 Parameters 인지 Tensor 인지 반드시 확인하시기 바랍니다.
import torch
norm = torch.FloatTensor([0])
for parameter in model.parameters():
norm += torch.norm(parameter, p=1)여하튼 위와 같이 L1 regularity 를 적용할 수 있는 train 함수를 만들었습니다. Check points 마다 l1 norm, l2 norm, training accuracy 를 출력합니다.
한가지, zero elements 의 개수를 계산하기 위하여 parameters 의 값이 0 이 아닌 변수의 개수를 세지 않았습니다. 대신 parameters 의 절대값 중 가장 큰 값의 sparse_threshold 배 보다 절대값의 크기가 작은 elements 의 개수를 세었습니다. PyTorch 로 구현한 Lasso Regression 의 coefficients 는 학습을 할수록 0 에 매우 가까워지지만, 0 이 되지는 않았습니다. 아마도 scikit-learn 의 구현체는 0 에 거의 가까워지면 그 값을 0 으로 치환하는 것이 아닐까 싶습니다. 실제로 모델을 학습하였을 떄 8.9893 * e-10 의 값이 존재하였지만, 0 은 존재하지 않았습니다. Logistic regression 의 classification 에서는 coefficient 의 절대값이 큰 변수들이 큰 영향력을 지닙니다. 그리고 절대값이 상대적으로 작은 변수들은 영향력이 적습니다. 그렇기 때문에 아래와 같이 coefficient 의 절대값의 sparse_threshold 배보다 작은 값들을 0 이라 생각했습니다.
def train(model, loss_func, optimizer, x, y, epochs,
c=1.0, penalty='l1', sparse_threshold=0.0005, use_gpu=False):
# for training error compute
y_true = y.numpy()
# regularity
c = torch.FloatTensor([c])
p = 1 if penalty == 'l1' else 2
# cuda
use_cuda = use_gpu and torch.cuda.is_available()
if use_cuda:
print('CUDA is {}available'.format('' if use_cuda else 'not '))
model = model.cuda()
x = x.cuda()
y = y.cuda()
c = c.cuda()
# Loop over all epochs
for epoch in range(epochs):
# clean gradient of previous epoch
optimizer.zero_grad()
# predict
y_pred = model(x)
# defining cost
loss = loss_func(y_pred, y)
regularity = torch.norm(model.fc.weight, p=p)
cost = loss + c * regularity
# back-propagation
cost.backward()
optimizer.step()
if epoch % 100 == 0 or epoch <= 10:
# training error
if use_cuda:
y_pred = y_pred.cpu()
y_pred = torch.argmax(y_pred, dim=1).numpy()
train_accuracy = accuracy(y_true, y_pred)
# informations
l1_norm = torch.norm(model.fc.weight, p=1)
l2_norm = torch.norm(model.fc.weight, p=2)
parameters = model.fc.weight.data.cpu().numpy().reshape(-1)
t = abs(parameters).max() * sparse_threshold
nz = np.where(abs(parameters) < t)[0].shape[0]
print('epoch = {}, training accuracy = {:.3}, l1={:.5}, l2={:.3}, nz={}'.format(
epoch, train_accuracy, l1_norm, l2_norm, nnz))
if use_cuda:
model = model.cpu()
return model이를 이용하여 앞서 만든 Logistic Regression 을 학습해 봅니다.
model = LogisticRegression(input_dim = 2 * n_features, n_classes = 2)
# loss function & optimizer
# Mean Squared Error loss
loss_func = nn.CrossEntropyLoss()
# Stochastic Gradient Descent optimizer
optimizer = optim.SGD(model.parameters(),lr=0.01, weight_decay=0.0)
model = train(
model,
loss_func,
optimizer,
torch.FloatTensor(x),
torch.LongTensor(y_true),
epochs=10000,
use_gpu=True,
c = 0.01
)중요한 부분들만을 아래에 기술하였습니다. 초반 10 번의 epochs 이 지나면 분류 성능은 완벽해 집니다. 그리고 random initializer 에 의하여 L1 norm 이 컸던 parameters 는 L1 regularity 에 의하여 계속 줄어듦을 볼 수 있습니다.
loss function 으로 Cross Entropy 를 이용하였습니다. Cross Entropy Loss 에서 data size 의 크기의 영향을 받지 않기 위해 size_average=True 로 설정하였습니다. 그렇기 때문에 Binary classification 에서는 최대 log (0.5) = 0.301 의 값을 지닙니다.
nn.CrossEntropyLoss(weight=None, size_average=True)만약 regularity coefficient 인 c 가 너무 크다면 loss 보다는 regularity 에만 집중하는 모델이 될 수 있습니다. 위 실험에서는 c=0.01 을 설정하였기 때문에 loss 와 regularity 가 어느 정도 균형이 맞습니다. 아래의 logs 를 살펴보면 대체로 L1 norm 이 26 수준에서 수렴합니다. c 를 곱하면 0.26 수준입니다.
그런데 epoch 을 늘릴수록 L1 norm 의 크기는 고정되는데 L2 norm 의 크기가 조금씩 증가합니다. 그리고 zero elements 의 개수도 증가합니다. 이는 몇 개의 elements 의 weight 의 크기를 키우고, 대부분의 weight 를 0 에 가깝게 보낸다는 의미입니다. (0.25, 0.25, 0.25, 0.25) 의 L1 norm 과 L2 norm 의 크기는 각각 1 과 0.5 입니다. 하지만 (0.5, 0.5, 0, 0) 의 L1 norm 과 L2 norm 의 크기는 각각 1 과 0.707 입니다. 극단적으로 (1, 0, 0, 0) 의 L1, L2 norm 은 모두 1 입니다. 아래의 logs 는 coefficients 가 점점 더 sparse 한 형태로 바뀌고 있음을 의미합니다.
epoch = 0, training accuracy = 0.489, l1=75.908, l2=0.805, nz=12
epoch = 1, training accuracy = 0.616, l1=74.749, l2=0.795, nz=14
epoch = 2, training accuracy = 0.713, l1=73.616, l2=0.787, nz=14
epoch = 3, training accuracy = 0.79, l1=72.511, l2=0.778, nz=16
epoch = 4, training accuracy = 0.854, l1=71.433, l2=0.77, nz=16
epoch = 5, training accuracy = 0.903, l1=70.377, l2=0.761, nz=19
epoch = 6, training accuracy = 0.947, l1=69.345, l2=0.753, nz=34
epoch = 7, training accuracy = 0.97, l1=68.333, l2=0.746, nz=34
epoch = 8, training accuracy = 0.987, l1=67.343, l2=0.738, nz=35
epoch = 9, training accuracy = 0.995, l1=66.369, l2=0.731, nz=40
epoch = 10, training accuracy = 0.998, l1=65.417, l2=0.724, nz=61
epoch = 100, training accuracy = 1.0, l1=28.686, l2=0.486, nz=635
epoch = 200, training accuracy = 1.0, l1=25.162, l2=0.49, nz=921
epoch = 300, training accuracy = 1.0, l1=25.048, l2=0.525, nz=1242
epoch = 400, training accuracy = 1.0, l1=25.256, l2=0.56, nz=1491
epoch = 500, training accuracy = 1.0, l1=25.452, l2=0.593, nz=1715
...
epoch = 1000, training accuracy = 1.0, l1=25.984, l2=0.718, nz=2612
epoch = 2000, training accuracy = 1.0, l1=26.285, l2=0.877, nz=3732
epoch = 3000, training accuracy = 1.0, l1=26.41, l2=0.981, nz=4646
epoch = 4000, training accuracy = 1.0, l1=26.464, l2=1.06, nz=5286
epoch = 5000, training accuracy = 1.0, l1=26.485, l2=1.11, nz=5647
epoch = 6000, training accuracy = 1.0, l1=26.505, l2=1.16, nz=6047
epoch = 7000, training accuracy = 1.0, l1=26.508, l2=1.2, nz=6438
epoch = 8000, training accuracy = 1.0, l1=26.508, l2=1.23, nz=6820
epoch = 9000, training accuracy = 1.0, l1=26.518, l2=1.26, nz=6965
epoch = 9900, training accuracy = 1.0, l1=26.516, l2=1.28, nz=7219
정리
이 포스트의 내용을 정리하면 아래와 같습니다.
- PyTorch 에서 L1 regularity 를 부여하기 위해서는 model 의 parameter 로부터 L1 norm 을 계산하여 이를 cost 에 더하면 됩니다. 단, Parameters 가 아닌 Tensor 를 더하면 안됩니다.
- L1 regularity 를 부여해도 coefficient 가 0 이 되지 않을 수 있습니다. Coefficient 의 절대값이 매우 작아지면 이를 0 으로 취급해도 됩니다.
- L1 norm 의 크기가 유지되면서 L2 norm 의 크기가 증가한다면, elements 중 절대값이 0 에 가까워지는 elements 의 개수가 늘어나고 있음을 의미합니다.