Random Projection and Locality Sensitive Hashing

k-nearest neighbor (k-NN) 문제는 모든 query 와 reference data 의 모든 점들 간의 거리를 계산하기 때문에 많은 거리 계산 비용과 정렬 비용이 든다고 알려져 있습니다. 하지만 approximated nearest neighbor search (ANNS) 방법들은 아주 조금 정확하지 않더라도 매우 빠르게 nearest neighbors 를 찾습니다. Locality Sensitive Hashing (LSH) 는 hashing 기반 방법으로, 가장 널리 이용되는 ANNS 입니다. 더 이상 k-NN 은 비싼 알고리즘이 아닙니다.

Nearest neighbor problem

최인접이웃 (nearest neighbors)은 regression, classification 에 이용되는 가장 기본적인 모델입니다. Non-parametric regression 은 주어진 query point 와 비슷한 점들의 y 값의 평균을 이용하여 regression 을 수행합니다.

$y(q) = \sum_{x \in K_q} w(q, x) \times y(x)$

where $w(q,x) = exp \left( -d(q, x) \right)$

Nearest neighbors 방법은 classification 에서는 Naive Bayes classifier 의 오차의 2 배 이하라고도 알려져 있으며, 가장 단순한 classifier 이기 때문에 다른 classifier 연구의 base model 로도 널리 사용됩니다. 일단 아주 직관적인 방법이기 때문에 이해도 쉽습니다.

그러나 하나의 query point 가 주어질 때 reference data 에서 가장 가까운 k 개의 점을 찾기 위해서는 모든 점들과의 거리를 계산해야 합니다. 만약 n 개의 점이 존재한다면 $O(n)$ 의 비용이 드는 매우 비싼 알고리즘이라 말합니다. 그러나 데이터의 크기가 커지면 절대 이런 brute-force 방법으로 계산을 하지 않습니다.

Approximated nearest neighbor search (ANNS) 란, 정확한 k 개의 최인접이웃을 찾지는 못하더라도, 비슷한 최인접이웃을 빠르게 찾기 위한 방법입니다. 이를 위한 방법은 다양합니다. i-Distance 같은 clustering 을 기반으로 하는 방법, random & neighbor network 를 함께 이용하는 네트워크 기반 방법, 혹은 tree 기반 방법들도 이용되었습니다. 이 다양한 방법들의 공통점은 벡터 공간을 단순한 공간으로 분할하여 이해한다는 것 (vector quantization) 입니다. 그 중에서도 hashing 기반 방법인 Locality Sensitive Hashing (LSH) 은 가장 널리 이용되는 방법입니다. 그리고 LSH 의 단점을 보완한 후속 연구들도 매우 많이 제안되었습니다.

Random Projection

Random Projection (RP) 를 이용하면 벡터 간의 거리를 보존하며 차원을 저차원으로 바꾸는 linear mapper 를 만들 수 있습니다. Random projection 은 Johnson-Linderstrauss Lemma 를 이용합니다. 아래의 식을 반드시 이해할 필요는 없습니다만, 중요한 식입니다. $0 < \epsilon < 1$ 일 때, $N$ 차원 인 $m$ 개의 points 가 있다면 $N$ 차원의 벡터를 $n > 8 \times ln(m) / \epsilon^2$ 인 n 차원으로 보낼 수 있는 linear mapper $f : \mathbb{R}^N \rightarrow \mathbb{R}^n$ 이 존재합니다.

$(1 - \epsilon) \rVert u - v \rVert ^2 \le \rVert f(u) - f(v) \rVert ^2 \le (1 + \epsilon) \rVert u - v \rVert ^2$

쉽게 설명하면 두 벡터 $u$ , $v$ 가 있을 때, 각각을 행렬 $M$ 를 곱하여 $x$ , $y$ 를 얻습니다. $x = Mu = f(u)$ , $y = Mv = f(v)$ 입니다. $x$ , $y$ 의 거리는 $u$ , $v$ 거리의 $(1 - \epsilon)$ 와 $(1 + \epsilon)$ 배수 안에 포함됩니다. 이런 성질을 만족시킬 수 있는 행렬 $M$ 이 존재한다는 것이 Johnson-Linderstrauss Lemma 입니다. 어떻게 구할 수 있는지는 나중에 이야기합니다. 만약 $u$ 가 1만 차원이고, $M$ 에 의하여 100차원인 $x$ 를 만들 수 있다면, 벡터 간 거리를 보존하며 100 배 적은 차원으로 차원 축소를 할 수 있습니다.

조금 만 더 알아봅시다. $x=Mu$ , $y=Mv$ 라면 $x \cdot y = u^T M^T M v$ 입니다. 만약 $M$ 의 각 column 이 직교 (orthogonal) 이고 각 column 이 L2 norm 이 1 인 unit vector 라면 $M^TM = I$ 입니다. 때문에 $x \cdot y = u \cdot v$ 입니다. 즉 $M$ 은 내적을 보존하는 linear mapper 입니다. $M$ 이 orthogonal matrix 가 아니라면 $M^T M = I + \epsilon$ 입니다. $\epsilon_{ij} = m_i ^T m_j$ 는 두 컬럼 $i$ , $j$ 의 내적입니다. 그런데 Kaski (1998) 의 논문을 보면 재밌는 실험이 있습니다. 평균이 0 인 random unit vector 를 column 으로 지닌 $M$ 을 만든 뒤, $\epsilon_{ij}$ 를 계산합니다. 그림의 d 는 각 random vector 의 차원입니다. Random vector 의 차원이 클수록 $\epsilon$ 의 절대값의 크기가 0 에 가까워집니다.

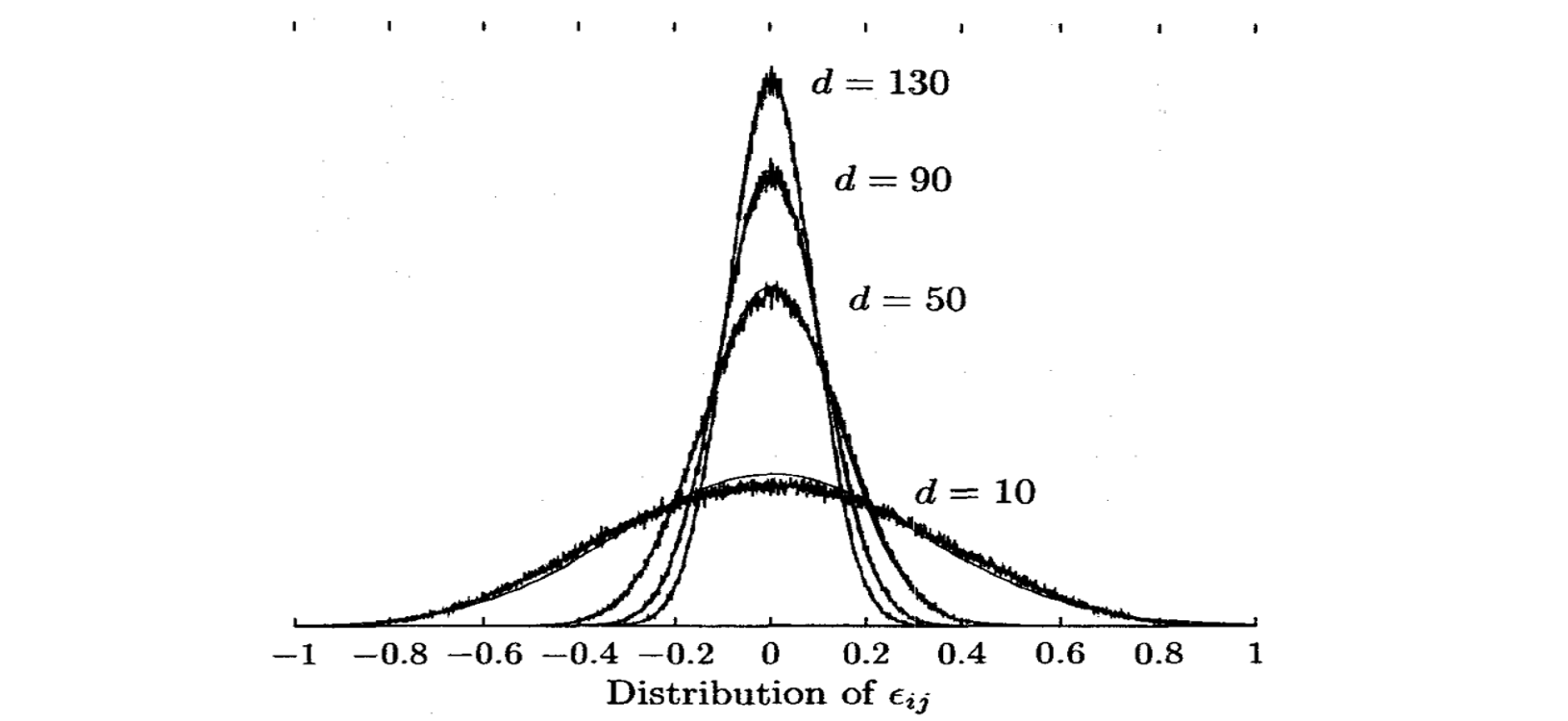
직관적인 해석은 다음과 같습니다. 두 개의 벡터를 random 하게 만들어 내적을 합니다. 두 벡터의 차원이 커질수록 내적의 값이 0 에 가까워집니다. 각 벡터의 elements 를 어떤 데이터라 생각할 경우, 두 벡터의 내적은 두 벡터의 elements 간의 covariance 입니다. 내적이 0 이면 covariance 가 0이라는 의미입니다. 두 벡터를 임의로 만들었습니다. 그렇기 때문에 두 벡터는 당연히 상관이 없죠. 그래서 내적, covariance 가 0 입니다. Random elements 10 개는 우연히도 상관이 있을 수도 있습니다. 하지만 50 개, 100 개 처럼 여러 개의 elements 를 만들수록 더더욱 상관이 없습니다.

$M$ 의 컬럼이 orthogonal 에 가까워질수록 $x \cdot y \simeq u \cdot v$ 가 됩니다.

Bingham & Mannila (2001) 은 Random Projection 과 Principal Components Analysis (PCA) 와의 거리 보존 능력에 대한 테스트를 수행하였습니다. 그 결과는 놀랍게도 거리 보존 능력은 PCA 보다도 RP 가 좋았습니다.

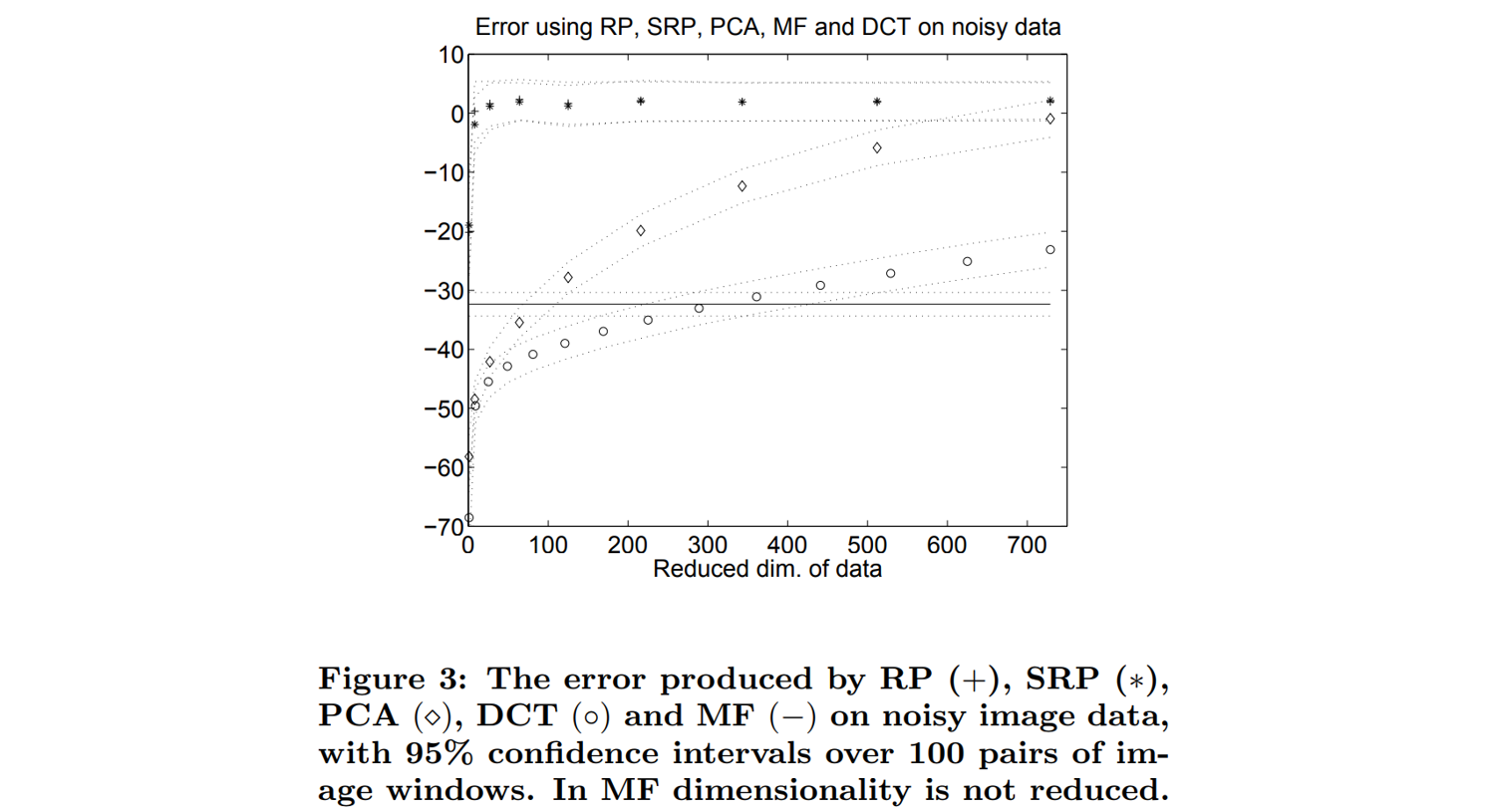
여러 번의 pairwise distance 계산이 필요할 때에는 데이터의 차원을 줄여두면 좋습니다. 비용이 $O(d^2 n^2)$ 이기 때문입니다. 대표적으로 clustering 알고리즘들이 여러 번의 pairwise distance 계산을 요구합니다. 이 때에 random projection 은 데이터의 차원을 줄이기 위해 전처리과정에서 이용되기도 합니다.

Locality Sensitve Hashing

Locality Sensitve Hashing (LSH) 은 Random Projection 을 이용하는 Approximated Nearest Neighbor Search (ANNS) 알고리즘입니다. Random Projection 이 어렵다면, 다음 사실만 기억해도 됩니다. $u$ 에 $M$ 을 곱하였더니 저차원 $x$ 를 얻었고, $u$ , $v$ 의 거리는 $x$ , $y$ 의 거리와 비슷하다라는 점만 기억해도 됩니다.

LSH 는 RP를 이용하여 각 data point 마다 각자가 속한 지역 주소를 부여합니다. 그림의 original vector 에 $M$ 을 곱하여 mapped vector 를 만듭니다. Original vector 가 비슷하였다면 mapped vector 도 비슷할 것입니다. 그런데 mapped vector 는 float 입니다. 소수점 버림을 하여 integer vector 로 변환합니다. 맨 위의 벡터는 [1, 0, 0] 이라는 label 을 가집니다. 2, 3 번째 벡터도 original vector 가 비슷하기 때문에 모두 [1, 0, 0] label 을 할당 받습니다. [1, 0, 0] 이 key 입니다. 같은 키를 지니는 벡터들을 한데 모아 bucket 을 만듭니다. 이 과정이 indexing 입니다.

저는 이 과정을 “우연이 계속되면 필연”이라는 말로 비유합니다. 두 개의 original vectors 가 각각 5 차원의 integer vector 로 바뀌었다고 상상해봅니다. 첫번째 integer 가 같다면 그럴 수 있습니다. 내적이 비슷한 벡터들은 많으니까요. 하지만 두번째 integer 도, 세번째 integer 도 같은 값을 가진다면, 우리는 두 벡터는 본래 비슷한 벡터가 아닌가? 라는 의심을 해야 합니다. 십중 팔구 비슷한 벡터였기 때문에 같은 integer keys 를 지닙니다. (하지만 십중 팔구 이므로, 같은 integer key 를 지녀도 서로 다른 벡터일 수 있습니다.)

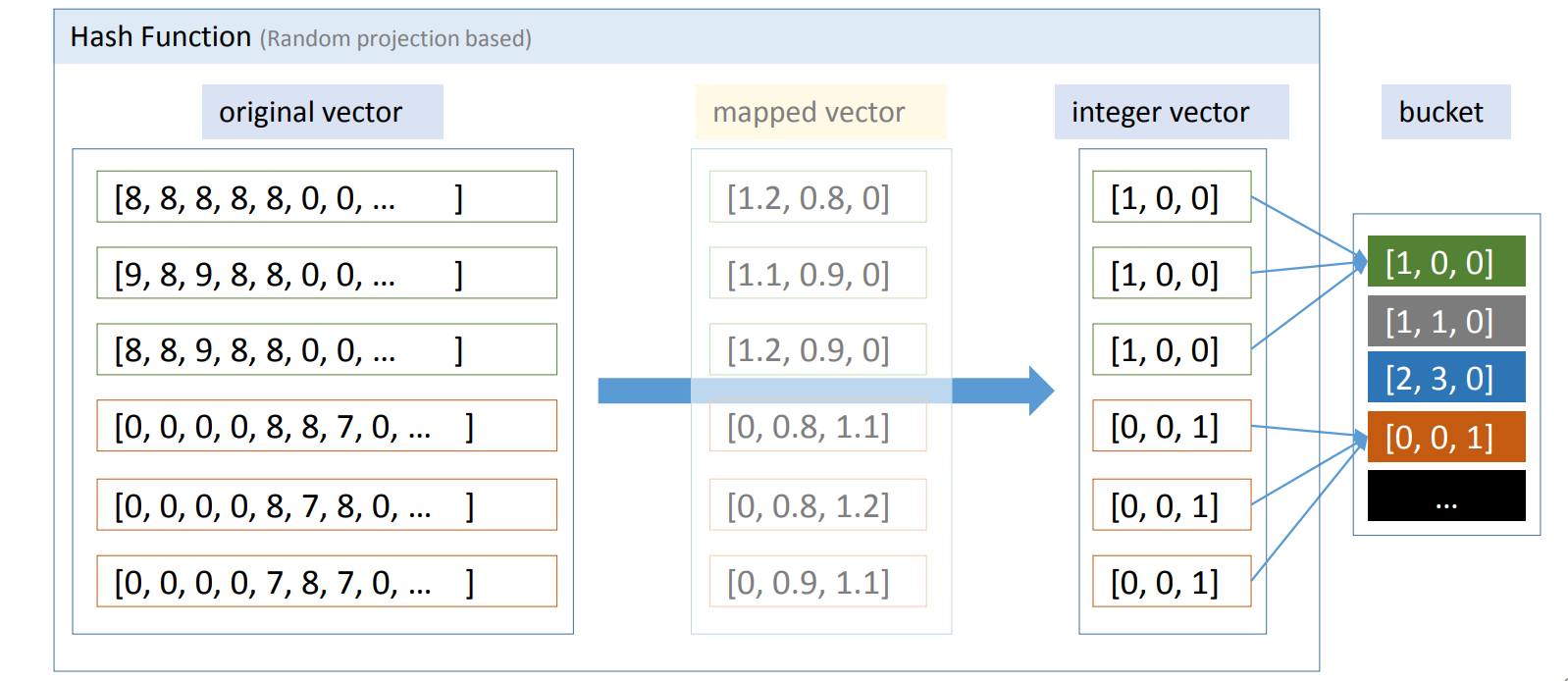
이제 query 와 비슷한 벡터들을 찾아봅시다. Query vector 에도 indexing 에 이용한 mapper $M$ 을 곱하고, integer vector 로 변환을 합니다. Query 도 [1, 0, 0] 의 key 를 얻었습니다. 그렇다면 bucket 에서 같은 [1, 0, 0] 의 키를 지닌 벡터들만 추려서 실제 거리를 계산합니다. 이는 ‘시 - 구 - 동’ 과 같은 구역체계에서 같은 ‘동’에 있는 data point 끼리만 거리를 계산하는 것입니다. 대부분의 벡터들은 다른 key 를 가지고 있기 때문에 불필요한 계산을 많이 줄였습니다. Original vector 가 비슷하면 key 가 비슷할 가능성이 높습니다. 만약 [1, 0, 0] 에 k 개 보다 적은 점이 포함되어 있다면 [1, 0, 0]과 비슷한 [1, 1, 0] 에서 추가적인 최인접이웃을 보강할 수도 있습니다.

이처럼 Original space 에서의 locality 를 고려하여 key 를 만드는 hashing 이라 하여 Locality Sensitive Hashing 이라 부릅니다.

Hashing function and its geometrical interpretation

Key 를 만드는 함수를 hashing function 이라 합니다. $g = (h_1, \cdots , h_m)$ 으로 기술합니다. $g$ 는 $m$ 차원의 integer key 를 만드는 함수입니다. 그리고 각 $h_i$ 는 다음 식과 같습니다. $a_i$ 는 original vector $x$ 와 차원의 크기가 같은 random unit vector 입니다. Gaussian disrtibution 으로 각 elements 를 생성합니다. $b_i$ 는 $[0, r]$ 사이의 random number 입니다. $x$ 는 random unit vector 와 내적을 한 뒤 $r$ 로 나눕니다. 그리고 이 값에 $[0, 1]$ 의 값을 뺀 뒤, 소수점 버림을 통하여 integer 를 만듭니다.

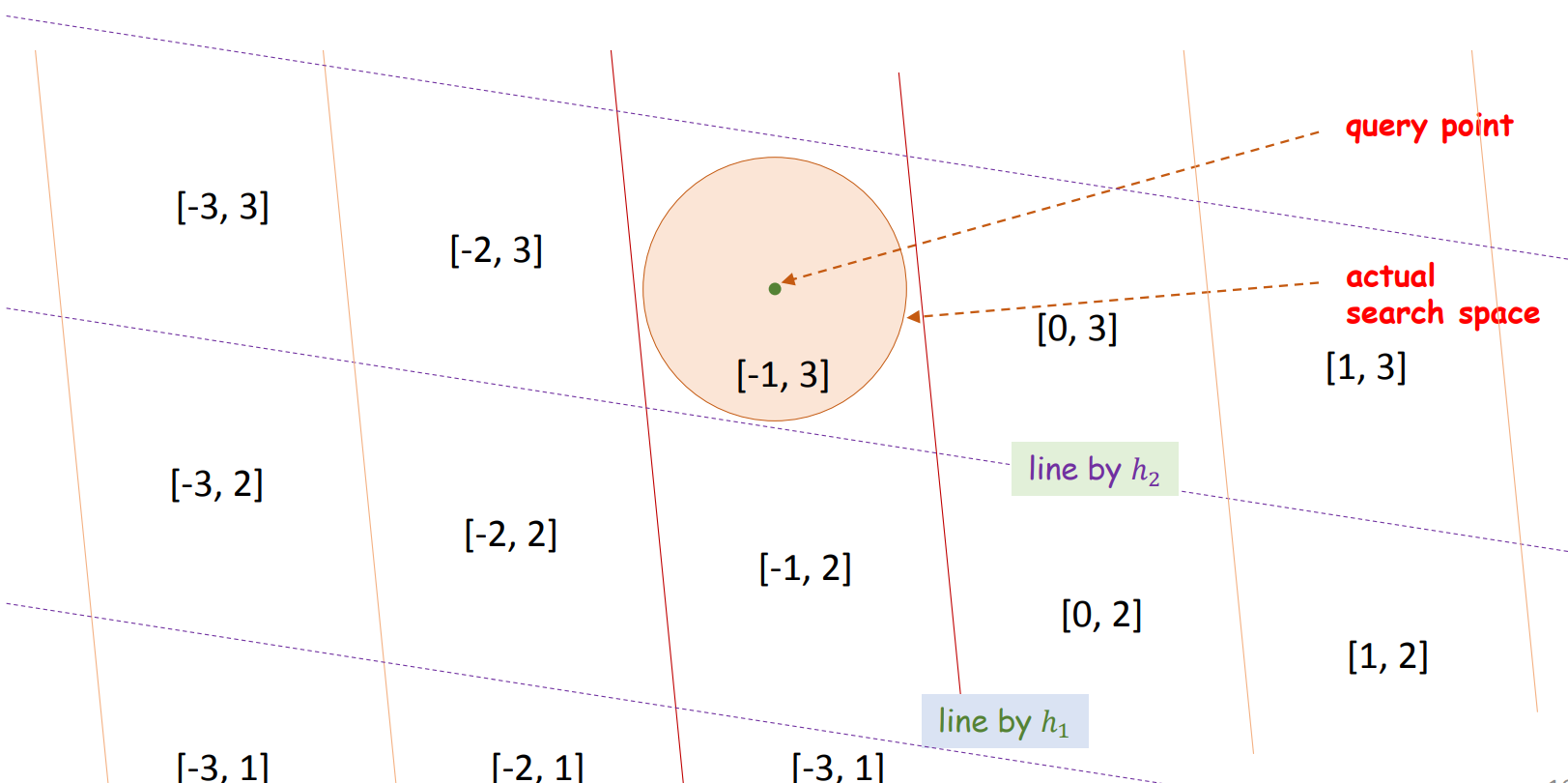
$h_i(x) = \lfloor \frac{a_i ^T x - b_i}{r} \rfloor = \lfloor \frac{a_i ^T x}{r} - \frac{b_i}{r} \rfloor$

$b_i$ 의 역할은 나중에 이야기하고, $a_i$ 를 기하학적으로 해석해봅니다. $h_1$ 에 의하여 같은 integer 를 지니는 공간이란, 평행한 선 ( $a_1$ ) 에 의하여 나뉘어지는 공간이라 생각할 수 있습니다. Query point 의 최인접이웃이 원 안에 포함(actual search space) 되어 있다면, $h_1$ 에 의하여 같은 integer 를 지니는 공간만 탐색하면 됩니다. 원이 [-1] 공간에 포함되어 있지만, 원 외에도 위/아래로 많은 공간이 포함되어 있습니다. 그리고 $r$ 은 평행선의 간격입니다.

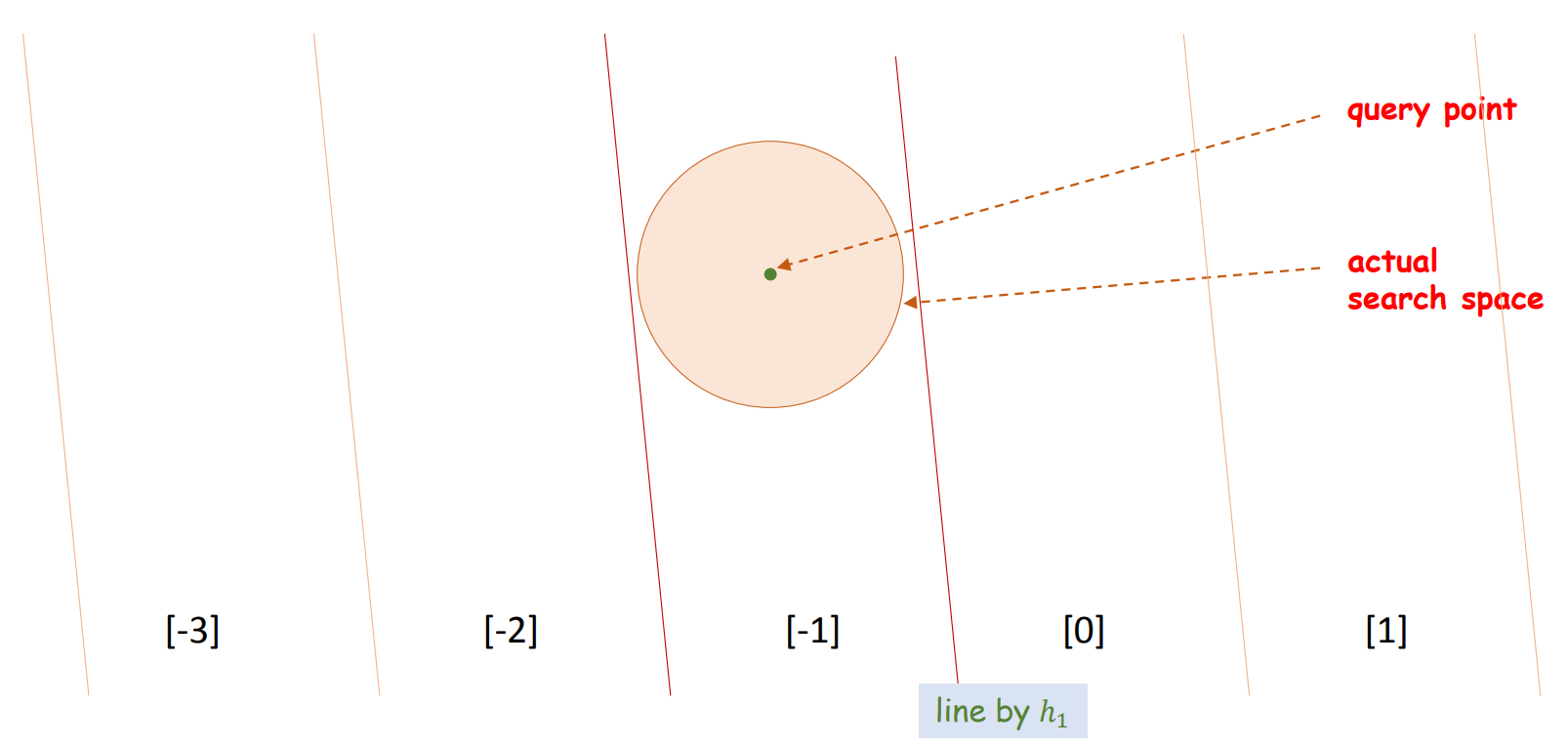
여기에 추가로 $h_2$ 를 적용합니다. Query point 는 [-1, 3] 의 key 를 지닙니다. 그리고 같은 키를 지니는 공간은 원을 포함합니다. 원 외의 공간은 매우 많이 줄어듭니다. $a_i$ 를 random vector 로 만들기 때문에 다양한 방향의 평면들로 공간이 나뉘어진 partition 이 만들어집니다. LSH 는 query point 에 대하여 같은 key 를 지니는 점들만 후보로 선택함으로써 효율적으로 최인접이웃의 후보를 제공합니다.

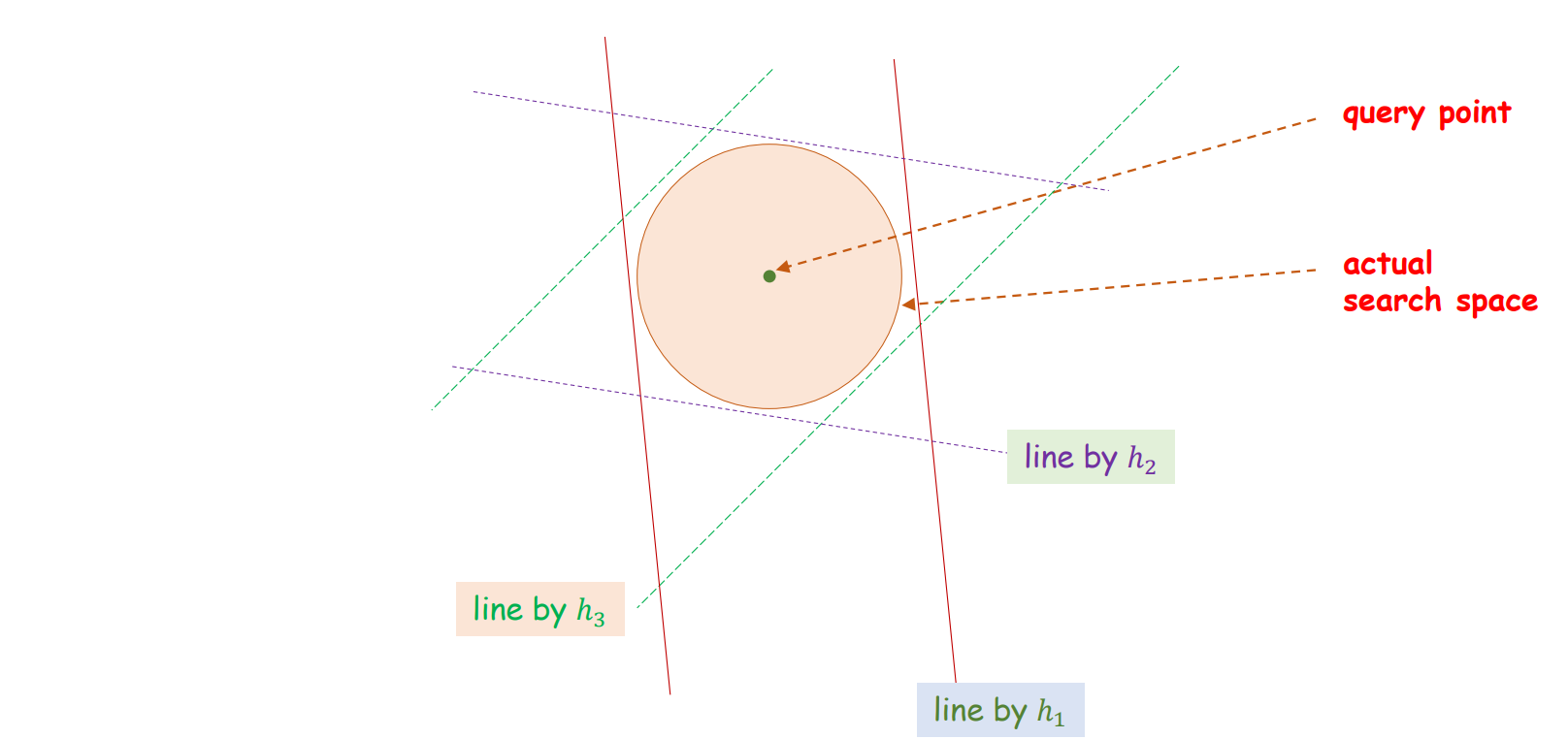
그러나 $h_i$ 를 많이 늘린다고하여 원에 가까운 bucket 이 만들어지지는 않습니다. 언제나 random 에는 한계가 있습니다. Integer vector 의 차원, $h_i$ 의 개수가 적당히 커야 효율적입니다. $h_i$ 의 개수를 늘린다고 partition 의 모양이 원에 한없이 가까워지지는 않습니다.

Multi-layers

그런데 hashing function $g$ 를 하나만 만들면 치명적인 문제가 발생합니다. Query point 가 하나의 $g$ 로 만들어지는 partition 의 모서리에 위치할 수 있습니다. Query point 의 최인접이웃이 위치하는 공간은 원인데, 원의 일부분만 탐색할 수도 있습니다.

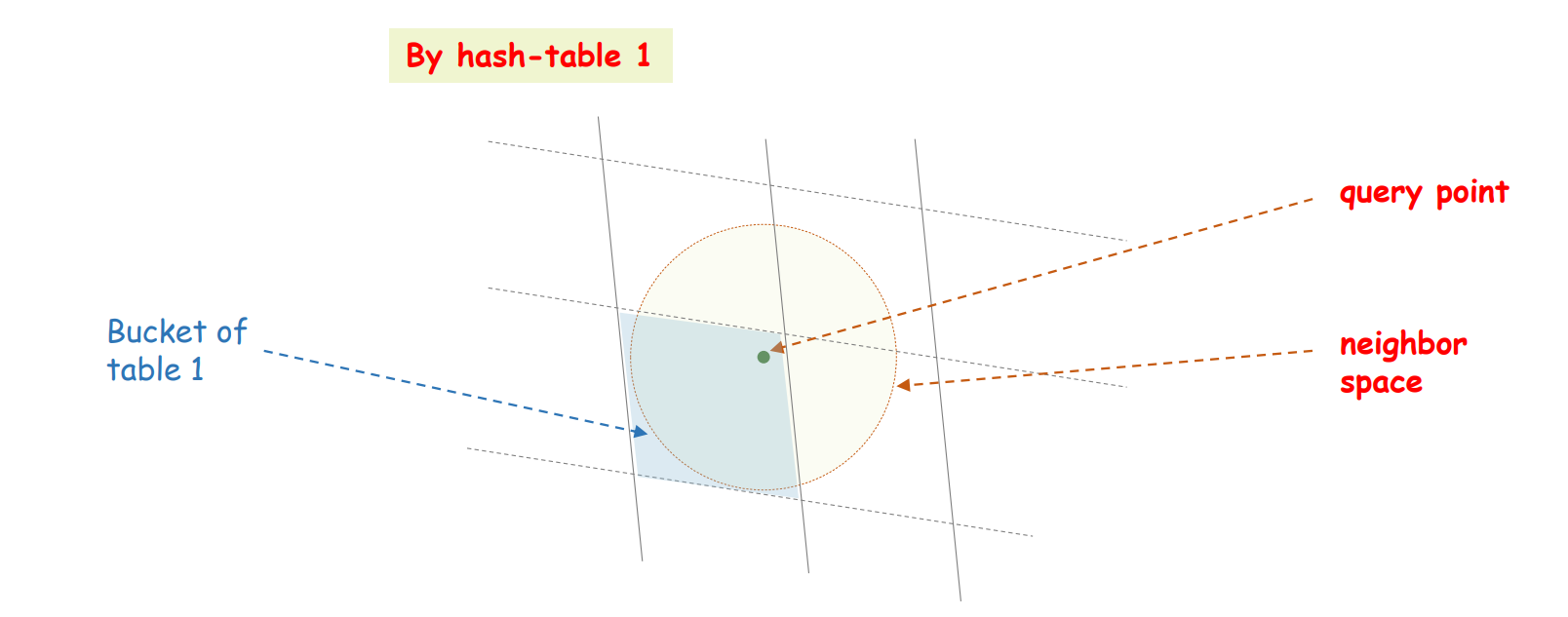
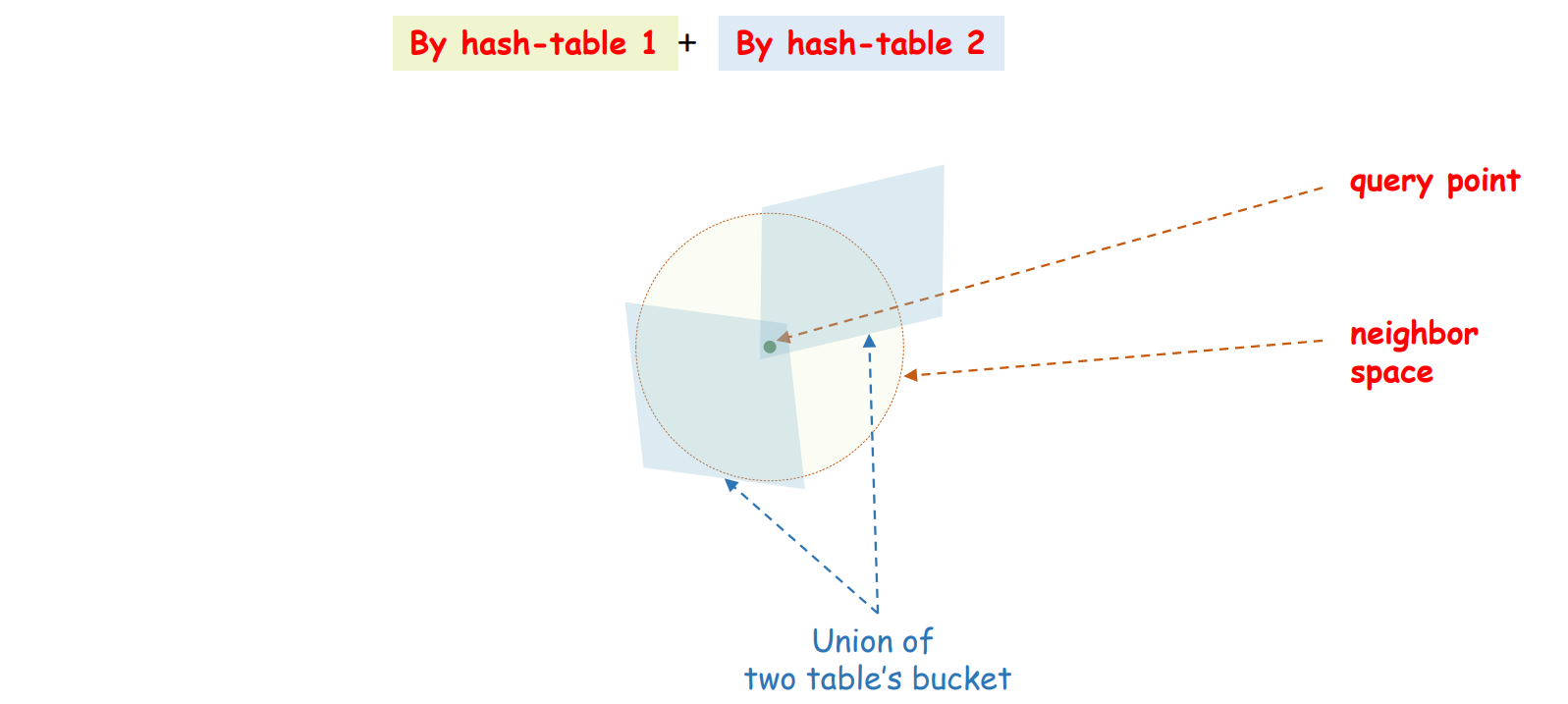
이를 방지하기 위해서 여러 개의 $g$ , 즉 여러 개의 layers (tables) 를 중첩하여 이용합니다. 어자피 모든 $h$ 를 random vector 로 만들기 때문에 또 다른 table, $g_2$ 는 아래 그림처럼 다른 방향의 격자로 공간을 나눈 buckets 이 됩니다.

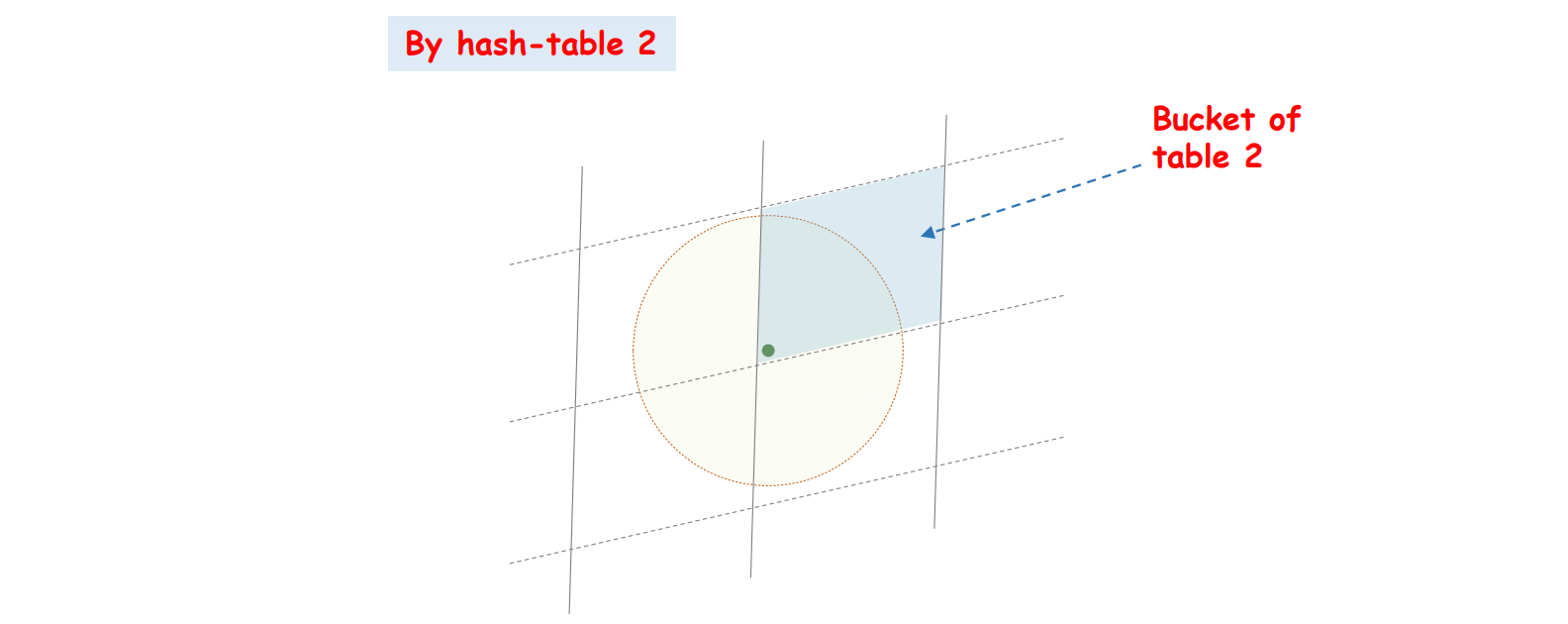
이 둘을 겹치면 좀 더 그럴싸한 탐색공간 (최인접이웃의 후보)을 확보할 수 있습니다.

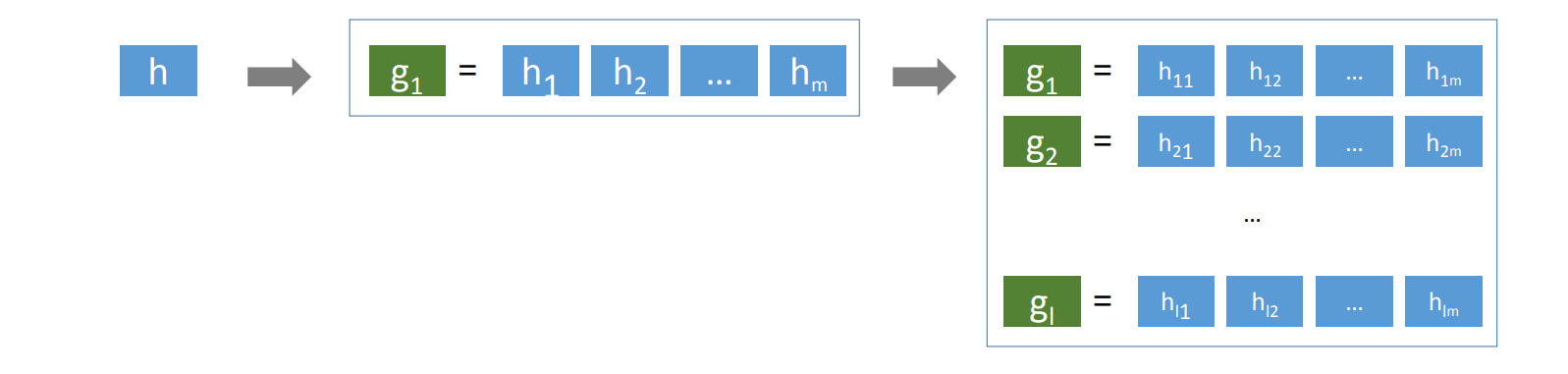
최종적인 구조는 다음과 같습니다. $x$ 를 $m$ 차원의 integer vector 로 변환하는 $g$ 가 $l$ 개 있습니다. $l$ 개의 hash table 을 이용합니다. 하나의 query point 에 대하여 $l$ 개의 hash table 로부터 최인접이웃의 후보를 가져온 뒤, 이들로부터 최종적인 최인접이웃을 구합니다. 후보들과 query point 간의 거리는 실제로 계산을 해야 합니다.

sklearn.neighbors.LSHForest

Scikit-learn 에도 LSH 가 구현되어 있습니다. 이번에는 random data 를 만들어 성능 테스트를 해보겠습니다. 50 차원의 인공데이터 100만개를 만듧니다.

import numpy as np

x = np.random.random_sample((1000000, 50))
x.shape # (1000000, 50)

LSHForest 에는 몇 가지 arguments 옵션이 있습니다. 그 중 n_estimators 는 hash table 의 개수, 즉 $g_i$ 의 개수입니다. 많이 늘린다고 성능이 좋아지지는 않습니다. radius 는 $r$ 에 해당합니다. 이 값을 잘 조절해야 하긴 하지만, 적당히 크게 잡고 n_candidates 를 조절해도 됩니다. n_candidates 는 각 hash table 마다 계산할 최소한의 최인접후보의 개수입니다.

from sklearn.neighbors import LSHForest

LSHForest(
    n_estimators=10,
    radius=1.0,
    n_candidates=50
)

Indexing 은 fit() 을 이용합니다. 100 만개의 데이터임에도 불구하고 인덱싱에 4 초가 걸리지 않습니다.

%%time

lsh = LSHForest(n_estimators=4)
lsh.fit(x)
# Wall time: 3.77 s

x 의 열 개의 점을 샘플링하여 5 개의 최인접이웃을 찾아봅니다. kneighbors() 함수를 이용하면 됩니다. 각 점들과의 거리인 dist 와 점들의 index 가 return 됩니다. 117 ms 만에 검색이 되었습니다.

%%time
dist, idxs = lsh.kneighbors(x[:10,], n_neighbors=5)
# Wall time: 117 ms

References

Bingham, E., & Mannila, H. (2001, August). Random projection in dimensionality reduction: applications to image and text data. In Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 245-250). ACM.
Kaski, S. (1998, May). Dimensionality reduction by random mapping: Fast similarity computation for clustering. In Neural Networks Proceedings, 1998. IEEE World Congress on Computational Intelligence. The 1998 IEEE International Joint Conference on (Vol. 1, pp. 413-418). IEEE.
Indyk, P., & Motwani, R. (1998, May). Approximate nearest neighbors: towards removing the curse of dimensionality. In Proceedings of the thirtieth annual ACM symposium on Theory of computing (pp. 604-613). ACM.