Hidden Markov Model (HMM) 은 품사 판별을 위하여 이용되기도 하였습니다. 특히 앞의 한 단계의 state 정보만을 이용하는 모델을 first-order HMM 이라 합니다. 그런데 이 first-order HMM 을 이용하는 품사 판별기의 품사열은 최단 경로 문제 기법으로도 구할 수 있습니다. 이번 포스트에서는 앞선 포스트에서 다뤘던 Ford algorithm 을 이용하여 품사를 판별하는 방법에 대하여 알아봅니다.
Review of Ford algorithm for shortest path
얼마 전, Hidden Markov Model (HMM) 을 기반으로 하는 품사 판별기의 코드를 공부하던 중, “findPath” 라는 이름의 함수를 보았습니다. HMM 의 decoding 과정을 설명할 때 주로 Dynamic programming 의 관점으로 설명을 하는데, 그 구현체는 최단 경로를 찾는 방법으로 decoding 과정을 설명하고 있었습니다. 생각해보니 first-order 를 따르는 HMM 이라면 최단 경로 문제와 동치가 됩니다. 이 이야기를 한 번 정리해야 겠다는 생각을 하였습니다.
이번 포스트에서는 HMM 에 대한 설명은 하지 않습니다. 조만간에 HMM 관련 포스트를 작성하고, 이 부분을 링크로 대체하도록 하겠습니다. 마디 (node) 와 호 (edge) 로 표현된 그래프에서 두 마디를 연결할 수 있는 경로 (path) 는 다양합니다. 그 중 거리가 가장 짧은 경로를 찾는 문제를 최단 경로 문제, shortest path 라 합니다.
Ford algorithm 은 매우 간단합니다. 목적지까지 가는 길에 조금 더 가까운 경로를 발견한다면, 내가 알고 있는 최단 경로를 그 경로로 계속하여 대체합니다. 더 이상 대체할 경로가 없다면 현재 알고 있는 경로가 최단 경로가 됩니다.
이를 위하여 Ford algorithm 의 초기화를 합니다. 출발지와 목적지가 주어지면, 출발지의 거리를 0 으로 설정합니다. 그리고 그 외의 모든 마디의 거리를 무한대로 설정합니다. 아직 어떤 마디까지도 가보지 않았기 때문에 실제로 얼마의 거리가 걸리는지를 알지 못합니다. 이제 모든 마디에 대해서 아래와 같은 조건이 만족하는 마디가 있는지 확인합니다.
if , then update
위 조건을 만족하는 경우가 없을 때 까지 반복하여 각 마디까지의 비용을 업데이트합니다.
이전 포스트에서 지하철 최단 경로 탐색을 위해 Ford algorithm 을 만드는 과정을 설명하였습니다. Ford algorithm 에 대한 자세한 설명은 위 포스트를 참고하세요. 이번 포스트는 Ford algorithm 에 대해서 알고 있다는 가정하에, 텍스트 처리에 대한 부분만 설명합니다.
예문과 사전
우리가 살펴볼 예문은 아래와 같습니다. 비문인 예문이지만, 쉬운 설명을 위해 아래의 예문을 이용합니다.
sentence = '청하는 아이오아이의 출신입니다'그리고 우리가 알고 있는 단어 사전은 아래와 같다고 가정합니다.
pos2words = {
'Noun': set('아이 아이오 아이오아이 청하 출신 청'.split()),
'Josa': set('은 는 이 가 의 를 을'.split()),
'Verb': set('청하 이 있 하 했 입'.split()),
'Eomi': set('다 었다 는 니다'.split())
}위 사전을 이용하여 위 문장을 다음과 같은 그래프로 표현할 수 있습니다. 그리고 올바른 품사 판별의 결과는 그림 위의 진한 선으로 연결된 경로로 표현할 수 있습니다. 아래 그림에서 BOS, EOS 는 Begin/End of Sentence 로, 문장의 시작과 끝을 표현하는 일반적인 표현입니다.
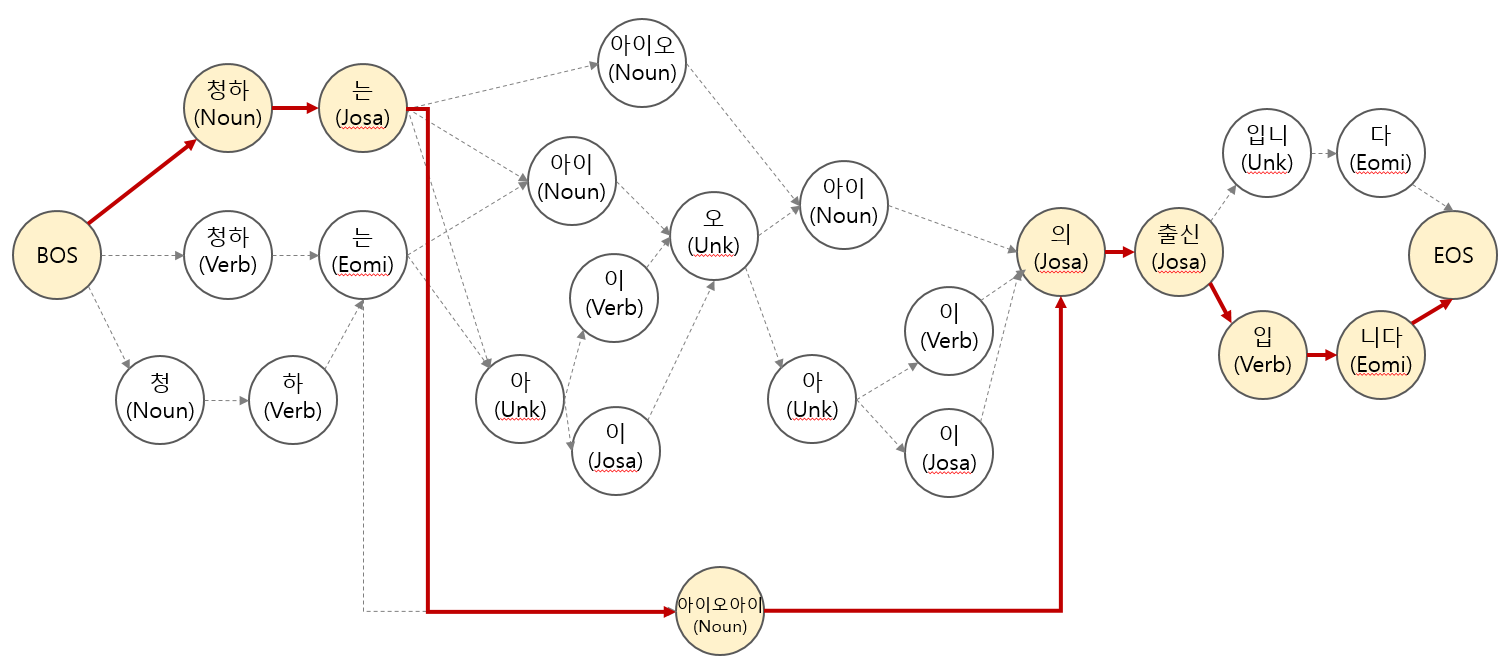
사실 품사 판별, 형태소 분석을 이야기하려면 한국어 용언의 활용과 복원에 대해서도 다뤄야 합니다. 하지만 이는 최단 경로를 이용한 품사 판별 원리를 설명하는데 반드시 필요한 부분이 아니므로, string slicing 만으로 단어 후보를 만들 수 있다고 가정합니다. 용언의 활용과 복원에 대해 궁금하신 분은 위의 링크를 참고하세요.
Lookup 을 위한 Dictionary 구현
우리는 어떤 단어가 주어졌을 때, 해당 단어의 품사를 확인하는 Dictionary 라는 class 를 만들것입니다. 이는 품사 판별 과정에서 단어/품사 후보를 만드는 기능을 합니다.
한 가지, 사전에 등록된 단어의 최대 길이를 확인하는 set_max_len 이라는 함수도 구현합니다.
class Dictionary:
def __init__(self, pos2words=None):
self.pos2words = pos2words if pos2words else {}
self.max_len = self._set_max_len()
def _set_max_len(self):
if not self.pos2words: return 0
return max((len(word) for words in self.pos2words.values() for word in words))
def get_pos(self, word):
return [pos for pos, words in self.pos2words.items() if word in words]
dictionary = Dictionary(pos2words)구현된 Dictionary 를 이용하여 두 단어에 대한 품사를 확인해 봅니다. get_pos 함수는 list of str 을 return 합니다. 만약 단어에 해당하는 품사가 없다면 [] 와 같은 empty list 를 return 합니다.
dictionary.get_pos('이') # ['Josa', 'Verb']
dictionary.get_pos('청하') # ['Noun', 'Verb']Lookup 을 이용한 마디 구성
앞서 만든 dictionary 를 이용하여 문장에서 아는 단어들을 인식합니다. 단어는 띄어쓰기가 포함되어 있지 않다고 가정합니다. 즉 n-gram 은 이번에는 고려하지 않습니다. 그렇다면 일단 띄어쓰기 기준으로 잘려진 어절에서 substring 을 찾은 뒤, dictionary 에 등록된 단어인지를 확인합니다.
eojeol_lookup 은 nested list 를 return 합니다. 이는 어절의 길이와 같은 길이입니다. List 의 각 칸은 각 위치에서의 단어를 의미합니다. Offset 은 문장에서의 단어의 위치를 표시하기 위한 값입니다.
def eojeol_lookup(eojeol, offset):
n = len(eojeol)
words = [[] for _ in range(n)]
for b in range(n):
for r in range(1, dictionary.max_len+1):
e = b+r
if e > n:
continue
sub = eojeol[b:e]
for pos in dictionary.get_pos(sub):
words[b].append((sub, pos, b+offset, e+offset))
return words
eojeol_lookup('청하는', offset=0)예를 들어 ‘청하는’ 이라는 어절에 offset=0 을 입력하면 아래와 같은 결과가 return 됩니다. List 의 첫번째 칸에는 ‘청/Noun’, ‘청하/Noun’, ‘청하/Verb’ 가 포함되어 있습니다. 그리고 문장에서의 각 단어의 시작과 끝점의 위치가 표시되어 있습니다. Offset=0 은 이 어절이 문장의 첫번째 어절이라는 의미입니다. Tuple 은 (단어, 품사, 문장 내 시작 위치, 문장 내 끝 위치) 로 구성되어 있습니다.
[[('청', 'Noun', 0, 1), ('청하', 'Noun', 0, 2), ('청하', 'Verb', 0, 2)],
[('하', 'Verb', 1, 2)],
[('는', 'Josa', 2, 3), ('는', 'Eomi', 2, 3)]]
만약 문장에서 해당 어절 앞에 3 글자가 더 있었다면 offset=3 으로 설정합니다.
eojeol_lookup('청하는', offset=3)그 결과, 단어는 동일하지만 단어의 위치가 다르게 표시됩니다.
[[('청', 'Noun', 3, 4), ('청하', 'Noun', 3, 5), ('청하', 'Verb', 3, 5)],
[('하', 'Verb', 4, 5)],
[('는', 'Josa', 5, 6), ('는', 'Eomi', 5, 6)]]
sent 라는 empty list 를 만든 뒤, 입력된 sentence 의 띄어쓰기 기준으로 eojeol_lookup 을 수행합니다. Offset 은 현재까지의 sent length 를 입력합니다.
def sentence_lookup(sentence):
sent = []
for eojeol in sentence.split():
sent += eojeol_lookup(eojeol, offset=len(sent))
return sent
sentence_lookup(sentence)sentence_lookup 함수를 이용하여 예문에 대한 lookup 을 수행하면 아래와 같은 결과를 얻을 수 있습니다. 아래의 tuple 은 이후 그래프에서의 마디가 됩니다.
[[('청', 'Noun', 0, 1), ('청하', 'Noun', 0, 2), ('청하', 'Verb', 0, 2)],
[('하', 'Verb', 1, 2)],
[('는', 'Josa', 2, 3), ('는', 'Eomi', 2, 3)],
[('아이', 'Noun', 3, 5), ('아이오', 'Noun', 3, 6), ('아이오아이', 'Noun', 3, 8)],
[('이', 'Josa', 4, 5), ('이', 'Verb', 4, 5)],
[],
[('아이', 'Noun', 6, 8)],
[('이', 'Josa', 7, 8), ('이', 'Verb', 7, 8)],
[('의', 'Josa', 8, 9)],
[('출신', 'Noun', 9, 11)],
[],
[('입', 'Verb', 11, 12)],
[('니다', 'Eomi', 12, 14)],
[('다', 'Eomi', 13, 14)]]
위의 nested list 에는 empty list 도 포함되어 있습니다. 이처럼 return type 을 만든 것은 마디 간 edge 를 쉽게 연결하기 위해서 입니다.
Edges 구성하기
연속된 단어 간 edges 와 Unk 간 edges
앞서 sentence_lookup 함수를 이용하여 그래프의 마디들을 만들었으니, 이번에는 이 마디들 간의 edge 를 만들 것입니다. 먼저 몇 가지 함수와 구문을 만듭니다.
sent 는 sentence_lookup 을 통하여 얻은 nested list 입니다.
chars = sentence.replace(' ', '')
sent.append([('EOS', 'EOS', n_char, n_char + 1)])
n_char = len(chars)
여기에 문장의 마지막을 표시하는 ‘EOS’ tuple 을 입력합니다. ‘EOS’의 위치는 문장의 길이보다 1 긴 위치에서 끝나도록 하였습니다.
get_nonempty_first(sent, offset) 는 sent 에서 offset 이후, 처음으로 empty list 가 아닌 index 를 출력합니다. get_nonempty_first(sent, offset=0) 를 실행하면 문장에서 처음으로 lookup 이 된 단어의 위치를 찾을 수 있습니다. 만약 이 위치 (nonempty_first) 가 0 보다 크다면 문장의 맨 앞부터 그 지점까지의 substring 이 그래프에 포함되어 있지 않다는 의미입니다. 그렇기 때문에 Unk 의 태그를 붙인 마디를 sent[0] 에 추가합니다.
def draw_edges(sentence):
chars = sentence.replace(' ', '')
sent = sentence_lookup(sentence)
n_char = len(chars)
sent.append([('EOS', 'EOS', n_char, n_char + 1)])
nonempty_first = get_nonempty_first(sent, offset=0)
if nonempty_first > 0:
sent[0].append((chars[:nonempty_first], 'Unk', 0, nonempty_first))
edges = forward_link(sent, chars)
edges = unk_link(edges, sent)
edges = add_bos(edges, sent)
edges = sorted(edges, key=lambda x:(x[0][2], x[0][3], x[1][2]))
return edges, sent
def get_nonempty_first(sent, offset=0):
for i in range(offset, len(sent)+1):
if sent[i]:
return i
return offset forward_link 함수는 문장 내에서 연속된 두 단어를 (앞의 단어 -> 뒤의 단어)로 연결하는 부분입니다. 예를 들어 (‘청하’, ‘Noun’, 0, 2) 는 문장 내에서 (0, 2)의 위치에 존재합니다. 이 단어는 시작점이 2 인 [(‘는’, ‘Josa’, 2, 3), (‘는’, ‘Eomi’, 2, 3)] 와 연결되어야 합니다. word 의 end position 을 찾은 뒤, sent[end] 에 다른 단어들이 존재하는지 살펴봅니다.
단어가 존재하지 않는다면 (if not sent[end]) end position 이후, 가장 처음으로 단어가 존재하는 구간까지를 Unk 의 태그를 붙인 단어로 graph 에 추가합니다. 사전에 ‘아이/Noun’ 은 등록되어 있지만, ‘오’는 어떤 품사로도 등록되어 있지 않습니다. 이 부분에서 때문에 ‘아이/Noun’ - ‘오/Unk’를 연결합니다. edges 에 ((‘아이’, ‘Noun’, 3, 5), (‘오’, ‘Unk’, 5, 6), 0)) 가 추가됩니다.
연결된 단어가 있다면 edges 에 그 두 단어를 (word, adjacent) 의 형태로 입력합니다. 이 때 edges 에 ((‘청하’, ‘Noun’, 0, 2), (‘는’, ‘Josa’, 2, 3)) 이 추가됩니다.
def forward_link(sent, chars):
edges = []
for words in sent[:-1]:
for word in words:
begin = word[2]
end = word[3]
if not sent[end]:
next_begin = get_nonempty_first(sent, end)
unk = (chars[end:next_begin], 'Unk', end, next_begin)
edges.append((word, unk))
else:
for adjacent in sent[end]:
edges.append((word, adjacent))
return edges앞서 ‘아이/Noun’ - ‘오/Unk’ 를 연결하였지만, ‘오/Unk’ - ‘아이/Noun’ 가 연결되지는 않았습니다. 이번에는 tag 가 ‘Unk’ 인 마디를 찾은 뒤, 이 단어의 end position 과 start position 이 같은 다른 단어를 연결합니다.
def unk_link(edges, sent):
unks = {node for _, node in edges if node[1] == 'Unk'}
for unk in unks:
for adjacent in sent[unk[3]]:
edges.append((unk, adjacent))
return edges마지막으로 문장의 맨 앞에 BOS 를 추가합니다.
def add_bos(edges, sent):
bos = ('BOS', 'BOS', -1, 0)
for word in sent[0]:
edges.append((bos, word))
return edges이 과정들을 합하여 draw_edges 함수를 만들었습니다.
edges, sent = draw_edges(sentence)draw_edges 함수에 예문을 넣은 결과입니다. dictionary 에 pos2words 에 의하여 등록된 단어 간, 그리고 Unk 단어 간의 edges 가 return 됩니다.
[(('BOS', 'BOS', -1, 0), ('청', 'Noun', 0, 1)),
(('BOS', 'BOS', -1, 0), ('청하', 'Noun', 0, 2)),
(('BOS', 'BOS', -1, 0), ('청하', 'Verb', 0, 2)),
(('청', 'Noun', 0, 1), ('하', 'Verb', 1, 2)),
(('청하', 'Noun', 0, 2), ('는', 'Josa', 2, 3)),
(('청하', 'Noun', 0, 2), ('는', 'Eomi', 2, 3)),
(('청하', 'Verb', 0, 2), ('는', 'Josa', 2, 3)),
(('청하', 'Verb', 0, 2), ('는', 'Eomi', 2, 3)),
(('하', 'Verb', 1, 2), ('는', 'Josa', 2, 3)),
(('하', 'Verb', 1, 2), ('는', 'Eomi', 2, 3)),
(('는', 'Josa', 2, 3), ('아이', 'Noun', 3, 5)),
(('는', 'Josa', 2, 3), ('아이오', 'Noun', 3, 6)),
(('는', 'Josa', 2, 3), ('아이오아이', 'Noun', 3, 8)),
(('는', 'Eomi', 2, 3), ('아이', 'Noun', 3, 5)),
(('는', 'Eomi', 2, 3), ('아이오', 'Noun', 3, 6)),
(('는', 'Eomi', 2, 3), ('아이오아이', 'Noun', 3, 8)),
(('아이', 'Noun', 3, 5), ('오', 'Unk', 5, 6)),
(('아이오', 'Noun', 3, 6), ('아이', 'Noun', 6, 8)),
(('아이오아이', 'Noun', 3, 8), ('의', 'Josa', 8, 9)),
(('이', 'Josa', 4, 5), ('오', 'Unk', 5, 6)),
(('이', 'Verb', 4, 5), ('오', 'Unk', 5, 6)),
(('오', 'Unk', 5, 6), ('아이', 'Noun', 6, 8)),
(('아이', 'Noun', 6, 8), ('의', 'Josa', 8, 9)),
(('이', 'Josa', 7, 8), ('의', 'Josa', 8, 9)),
(('이', 'Verb', 7, 8), ('의', 'Josa', 8, 9)),
(('의', 'Josa', 8, 9), ('출신', 'Noun', 9, 11)),
(('출신', 'Noun', 9, 11), ('입', 'Verb', 11, 12)),
(('입', 'Verb', 11, 12), ('니다', 'Eomi', 12, 14)),
(('니다', 'Eomi', 12, 14), ('EOS', 'EOS', 14, 15)),
(('다', 'Eomi', 13, 14), ('EOS', 'EOS', 14, 15))]
Weight 부여
이제 연결한 edges 에 weight 를 부여해야 합니다. 매우 간단한 edge weight 의 규칙을 한 가지 만들어봅니다. 만약 연결된 두 마디의 품사가 (‘Noun’, ‘Josa’) 이면 0.7 점을 부여합니다. 그 외의 다른 품사 쌍에 대한 점수를 transition 에 부여합니다. 여기에 포함되지 않는 품사 쌍의 점수는 0 점입니다.
또한 각 (단어, 품사) 에 대한 점수도 부여할 수 있습니다. (‘아이오아이’, ‘Noun’) 일 경우에는 0.5 점을, (‘청하’, ‘Noun’) 일 경우에는 0.2 점을 부여합니다.
transition = {
('Noun', 'Josa'): 0.7,
('Noun', 'Noun'): 0.3,
('Verb', 'Eomi'): 0.5,
('Verb', 'Noun'): 0.5,
('Verb', 'Josa'): -0.1,
}
generation = {
'Noun': {
'아이오아이': 0.5,
'청하': 0.2,
}
}이로부터 우리는 두 마디 간 edge 의 weight 를 계산하는 함수를 만들 수 있습니다. ((‘청하’, ‘Noun’, 0, 2), (‘는’, ‘Josa’, 2, 3)) 이라는 edge 가 cost 함수에 입력되었을 때, 품사 쌍이 transition 에 포함되어 있는지 get 함수를 이용하여 탐색합니다.
score = transition.get((edge[0][1], edge[1][1]), 0)(단어, 품사)에 대한 점수는 두번째 마디에 대해서만 계산합니다. 이전에 계산한 score 에 해당 점수를 더합니다.
score += generation.get(edge[1][1], {}).get(edge[1][0], 0)이 과정을 정리하여 Weighter 라는 class 로 만듭니다. init 함수의 argument 는 transition 과 generation 이라는 점수표 입니다. 그리고 비용 (cost) 은 점수 (score) 에 -1 을 곱한 값을 이용합니다. 이 값이 edge weight 입니다.
class Weighter:
def __init__(self, transition, generation):
self.transition = transition
self.generation = generation
def cost(self, edge):
score = 0
score += self.transition.get((edge[0][1], edge[1][1]), 0)
score += self.generation.get(edge[1][1], {}).get(edge[1][0], 0)
return -1 * score
weighter = Weighter(transition, generation)이를 이용하여 앞서 만든 edges 의 한 edge 의 weight 를 계산하였습니다.
print(edges[4]) # (('청하', 'Noun', 0, 2), ('는', 'Josa', 2, 3))
print(weighter.cost(edges[4])) # -0.7모든 edges 에 대하여 weight 를 추가합니다.
def attach_weight(edges):
edges = [(edge[0], edge[1], weighter.cost(edge)) for edge in edges]
return edges
edges = attach_weight(edges)그 결과는 아래와 같습니다.
[(('BOS', 'BOS', -1, 0), ('청', 'Noun', 0, 1), 0),
(('BOS', 'BOS', -1, 0), ('청하', 'Noun', 0, 2), -0.2),
(('BOS', 'BOS', -1, 0), ('청하', 'Verb', 0, 2), 0),
(('청', 'Noun', 0, 1), ('하', 'Verb', 1, 2), 0),
(('청하', 'Noun', 0, 2), ('는', 'Josa', 2, 3), -0.7),
(('청하', 'Noun', 0, 2), ('는', 'Eomi', 2, 3), 0),
(('청하', 'Verb', 0, 2), ('는', 'Josa', 2, 3), 0.1),
(('청하', 'Verb', 0, 2), ('는', 'Eomi', 2, 3), -0.5),
(('하', 'Verb', 1, 2), ('는', 'Josa', 2, 3), 0.1),
(('하', 'Verb', 1, 2), ('는', 'Eomi', 2, 3), -0.5),
(('는', 'Josa', 2, 3), ('아이', 'Noun', 3, 5), 0),
(('는', 'Josa', 2, 3), ('아이오', 'Noun', 3, 6), 0),
(('는', 'Josa', 2, 3), ('아이오아이', 'Noun', 3, 8), -0.5),
(('는', 'Eomi', 2, 3), ('아이', 'Noun', 3, 5), 0),
(('는', 'Eomi', 2, 3), ('아이오', 'Noun', 3, 6), 0),
(('는', 'Eomi', 2, 3), ('아이오아이', 'Noun', 3, 8), -0.5),
(('아이', 'Noun', 3, 5), ('오', 'Unk', 5, 6), 0),
(('아이오', 'Noun', 3, 6), ('아이', 'Noun', 6, 8), -0.3),
(('아이오아이', 'Noun', 3, 8), ('의', 'Josa', 8, 9), -0.7),
(('이', 'Josa', 4, 5), ('오', 'Unk', 5, 6), 0),
(('이', 'Verb', 4, 5), ('오', 'Unk', 5, 6), 0),
(('오', 'Unk', 5, 6), ('아이', 'Noun', 6, 8), 0),
(('아이', 'Noun', 6, 8), ('의', 'Josa', 8, 9), -0.7),
(('이', 'Josa', 7, 8), ('의', 'Josa', 8, 9), 0),
(('이', 'Verb', 7, 8), ('의', 'Josa', 8, 9), 0.1),
(('의', 'Josa', 8, 9), ('출신', 'Noun', 9, 11), 0),
(('출신', 'Noun', 9, 11), ('입', 'Verb', 11, 12), 0),
(('입', 'Verb', 11, 12), ('니다', 'Eomi', 12, 14), -0.5),
(('니다', 'Eomi', 12, 14), ('EOS', 'EOS', 14, 15), 0),
(('다', 'Eomi', 13, 14), ('EOS', 'EOS', 14, 15), 0)]
list of tuple 로 이뤄진 edges 를 dict dict 형식의 그래프로 변환합니다. tuple 의 첫번째 tuple 을 source 로, 두번째 tuple 을 destination 으로 정리합니다.
from collections import defaultdict
from pprint import pprint
def edges_to_dict(edges):
g = defaultdict(lambda: {})
for from_, to_, weight in edges:
g[from_][to_] = weight
return dict(g)
g = edges_to_dict(edges)
pprint(g)그 결과 아래와 같은 형식의 그래프 g 를 만들 수 있습니다. 앞선 포스트의 그래프 형식과 동일합니다.
g = {
('BOS', 'BOS', -1, 0): {
('청', 'Noun', 0, 1): 0,
('청하', 'Noun', 0, 2): -0.2,
('청하', 'Verb', 0, 2): 0
},
('청하', 'Noun', 0, 2): {
('는', 'Eomi', 2, 3): 0,
('는', 'Josa', 2, 3): -0.7
},
('청하', 'Verb', 0, 2): {
('는', 'Eomi', 2, 3): -0.5,
('는', 'Josa', 2, 3): 0.1
},
...
}
Ford algorithm 을 이용한 품사 판별기 만들기
우리는 이 그래프를 이용하여 앞서 만든 ford algorithm 을 적용하였습니다.
bos = ('BOS', 'BOS', -1, 0)
eos = ('EOS', 'EOS', 14, 15)
ford(g, start = bos, destination = eos)아래는 Ford algorithm 에 의하여 비용이 바뀌는 모습입니다.
cost[('는', 'Eomi', 2, 3) -> ('아이오아이', 'Noun', 3, 8)] = 24.200000000000003 -> 23.700000000000003
cost[('아이오아이', 'Noun', 3, 8) -> ('의', 'Josa', 8, 9)] = 24.200000000000003 -> 23.000000000000004
cost[('BOS', 'BOS', -1, 0) -> ('청하', 'Noun', 0, 2)] = 24.200000000000003 -> -0.2
cost[('BOS', 'BOS', -1, 0) -> ('청하', 'Verb', 0, 2)] = 24.200000000000003 -> 0
cost[('BOS', 'BOS', -1, 0) -> ('청', 'Noun', 0, 1)] = 24.200000000000003 -> 0
cost[('아이오', 'Noun', 3, 6) -> ('아이', 'Noun', 6, 8)] = 24.200000000000003 -> 23.900000000000002
cost[('입', 'Verb', 11, 12) -> ('니다', 'Eomi', 12, 14)] = 24.200000000000003 -> 23.700000000000003
cost[('니다', 'Eomi', 12, 14) -> ('EOS', 'EOS', 14, 15)] = 24.200000000000003 -> 23.700000000000003
cost[('의', 'Josa', 8, 9) -> ('출신', 'Noun', 9, 11)] = 24.200000000000003 -> 23.000000000000004
cost[('하', 'Verb', 1, 2) -> ('는', 'Eomi', 2, 3)] = 24.200000000000003 -> 23.700000000000003
cost[('청하', 'Noun', 0, 2) -> ('는', 'Eomi', 2, 3)] = 23.700000000000003 -> -0.2
cost[('청하', 'Noun', 0, 2) -> ('는', 'Josa', 2, 3)] = 24.200000000000003 -> -0.8999999999999999
cost[('청하', 'Verb', 0, 2) -> ('는', 'Eomi', 2, 3)] = -0.2 -> -0.5
cost[('는', 'Josa', 2, 3) -> ('아이오아이', 'Noun', 3, 8)] = 23.700000000000003 -> -1.4
cost[('는', 'Josa', 2, 3) -> ('아이오', 'Noun', 3, 6)] = 24.200000000000003 -> -0.8999999999999999
cost[('는', 'Josa', 2, 3) -> ('아이', 'Noun', 3, 5)] = 24.200000000000003 -> -0.8999999999999999
cost[('출신', 'Noun', 9, 11) -> ('입', 'Verb', 11, 12)] = 24.200000000000003 -> 23.000000000000004
cost[('아이', 'Noun', 3, 5) -> ('오', 'Unk', 5, 6)] = 24.200000000000003 -> -0.8999999999999999
cost[('청', 'Noun', 0, 1) -> ('하', 'Verb', 1, 2)] = 24.200000000000003 -> 0
cost[('아이오아이', 'Noun', 3, 8) -> ('의', 'Josa', 8, 9)] = 23.000000000000004 -> -2.0999999999999996
cost[('아이오', 'Noun', 3, 6) -> ('아이', 'Noun', 6, 8)] = 23.900000000000002 -> -1.2
cost[('입', 'Verb', 11, 12) -> ('니다', 'Eomi', 12, 14)] = 23.700000000000003 -> 22.500000000000004
cost[('니다', 'Eomi', 12, 14) -> ('EOS', 'EOS', 14, 15)] = 23.700000000000003 -> 22.500000000000004
cost[('의', 'Josa', 8, 9) -> ('출신', 'Noun', 9, 11)] = 23.000000000000004 -> -2.0999999999999996
cost[('출신', 'Noun', 9, 11) -> ('입', 'Verb', 11, 12)] = 23.000000000000004 -> -2.0999999999999996
cost[('입', 'Verb', 11, 12) -> ('니다', 'Eomi', 12, 14)] = 22.500000000000004 -> -2.5999999999999996
cost[('니다', 'Eomi', 12, 14) -> ('EOS', 'EOS', 14, 15)] = 22.500000000000004 -> -2.5999999999999996
그 결과 아래와 같은 비용과 path 가 만들어집니다. 예시 문장은 [(‘청하’, ‘Noun’), (‘는’, ‘Josa’), (‘아이오아이’, ‘Noun’), (‘의’, ‘Josa’), (‘출신’, ‘Noun’), (‘입’, ‘Verb’), (‘니다’, ‘Eomi’)] 로 품사 판별이 이뤄집니다.
'cost': 2.5999999999999996
[[('BOS', 'BOS', -1, 0),
('청하', 'Noun', 0, 2),
('는', 'Josa', 2, 3),
('아이오아이', 'Noun', 3, 8),
('의', 'Josa', 8, 9),
('출신', 'Noun', 9, 11),
('입', 'Verb', 11, 12),
('니다', 'Eomi', 12, 14),
('EOS', 'EOS', 14, 15)]]}
앞서 최단 경로를 찾는 알고리즘은 Ford 외에도 Dijkstra 도 있다 하였습니다만, Dijkstra 는 edge weight 가 반드시 0 이상이어야 합니다. Weighter 를 구현하기에 따라 음의 edge weight 가 만들어질 수도 있기 때문에 안전하게 Ford algorithm 을 이용하였던 것입니다.
Hidden Markov Model (HMM) 과의 관계
Hidden Markov Model (HMM) 를 이용하면 길이가 인 sequence 에 대하여 가 가장 큰 를 찾을 수 있습니다. 이 과정을 HMM 의 decoding 이라 합니다. 이 때 는 다음처럼 계산됩니다.
위 식의 계산 과정과 원리는 HMM 관련 포스트에서 다루겠습니다.
숫자 계산에서 곱셈은 덧셈보다 비싼 작업입니다. 그렇기 때문에 확률을 곱하는 작업들은 주로 log 를 씌워 덧셈으로 변환합니다. 위 수식은 아래처럼 변환됩니다.
그런데 가장 큰 를 찾는 것은 가장 작은 를 찾는 것과 같습니다.
또한 위 식을 정리하면 각 index 별로 묶을 수 있습니다. 은 sequence 가 시작하여 이 발생하기 위한 확률입니다. 그리고 는 다음에 가 발생할 확률입니다. 이를 각각 (START, ) 이 연결된 이득, (, ) 이 연결된 이득으로 생각할 수 있습니다. 그리고 각각을 그래프의 마디로 생각하면 (, ) 의 비용을 로 생각할 수 있습니다.
이는 우리가 앞서 정의한 transition 과 generation 을 각각 와 로 생각한다면 결국 HMM 에서 확률이 가장 큰 을 찾는 것은 그래프에서 비용이 가장 작은 를 연결하는 path 를 찾는 것과 같습니다.