마디 (node) 와 호 (edge) 로 표현된 그래프에서 두 마디를 연결할 수 있는 경로 (path) 는 다양합니다. 그 중 거리가 가장 짧은 경로를 찾는 문제를 최단 경로 문제, shortest path 라 합니다. 이번 포스트에서는 최단 경로를 찾는 방법 중 하나인 Ford algorithm 에 대하여 알아보고, Python 으로 이를 간단히 구현합니다.
Shortest path problem and Hidden Markov Model
학부 시절 들었던 과목 중, 아직도 기억이 남는 과목들이 있습니다. 홍성필 교수님의 경영 과학은 제일 좋아했던 과목 중 하나입니다. 이 과목에서는 최단 경로 문제 외에도 심플렉스와 같은 최적화 알고리즘들에 대해 배울 수 있습니다. 명료한 문제 정의와 해법을 찾아가는 직관들이 매력적이었습니다. 그리고 대학원에서는 데이터 마이닝과 머신 러닝을 공부하였는데, ISOMAP 과 같은 알고리즘은 최단 경로를 알아야 합니다. 한창 ISOMAP 과 같은 임베딩 방법들을 공부할 때면 늘 경영 과학이 생각났었습니다.
최단 경로 문제는 그래프에서 두 마디 간의 경로 중 가장 짧은 경로를 찾는 문제입니다. 이는 우리 주변에서 자주 접하는 문제입니다. 지하철의 출발지와 도착지 사이에서의 최소 환승 경로, 최소 시간 경로가 대표적인 예시입니다. 우리가 이 포스트에서 살펴볼 예시 그래프 중 하나도 지하철 노선도의 축약본 입니다.
대표적인 최단 경로를 탐색하는 알고리즘은 Bellman - Ford 와 Dijkstra 가 있습니다. Bellman - Ford 는 그래프의 호 간의 비용 (혹은 거리)에 음수가 존재할 경우에도 적용할 수 있는 방법이며, Dijkstra 는 호 간의 비용이 모두 0 이상인 경우에만 적용할 수 있는 방법입니다. 우리는 이 두 가지 방법 중 Ford algorithm 에 대해서만 이야기하려 합니다.
이번 포스트에서 사용할 예시 그래프는 홍성필 교수님의 저서, “경영과학”의 예시를 이용하였음을 밝힘니다. “경영과학” 책은 정말로 좋아하는 책 중 하나입니다. 제가 수업을 들을 때에는 책이 출간되지는 않았습니다. 교수님이 작성 중이시던 원고를 이용하여 수업을 하였는데, 초판이 나온 다음, 보관하고 싶어 따로 책을 샀었습니다. 그런데 그랬던 사람들이 저 뿐 아니라 여럿 있었던 기억이 납니다. 그만큼 좋은 책이니 경영과학에 대해 관심이 있으신 분들에게 추천합니다.
지하철 최단 거리 경로 예시, Undirected graph
지하철 노선도 축약본은 홍성필 교수님의 저서의 예시입니다. 이 그래프는 아래 그램과 같습니다.
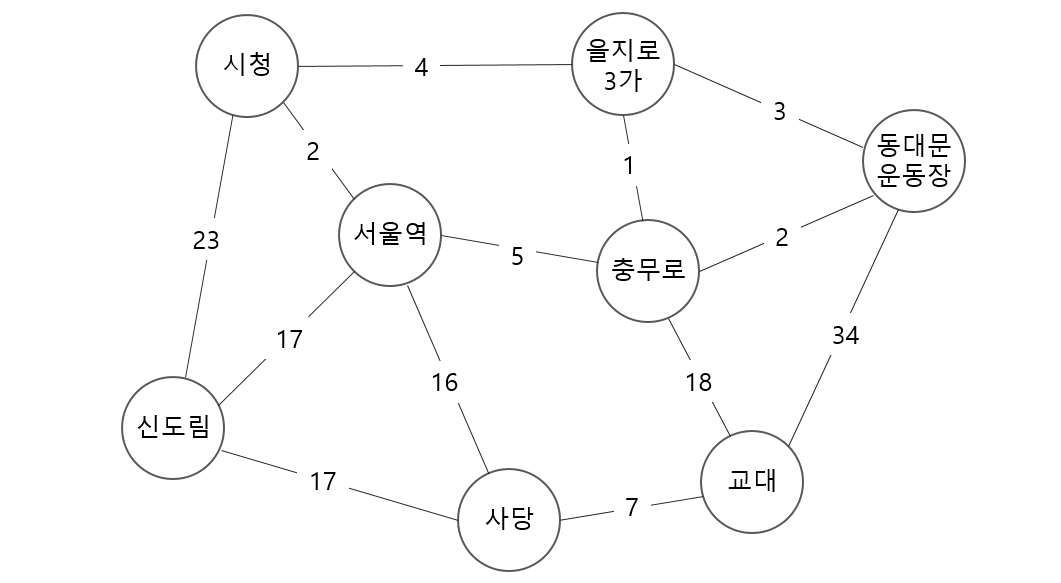
그래프를 데이터로 표현하는 방식은 다양합니다. Sparse matrix 도 그래프를 표현하는 방법 중 하나입니다. Row idx 를 출발점, column idx 를 도착점으로 생각하면 (row, column) 의 값은 edge weight 가 됩니다. 그리고 모든 마디가 연결된 것은 아니기 때문에, 연결되지 않은 마디는 edge weight 가 0 이도록 표현합니다.
혹은 dict dict 로 표현할 수도 있습니다. 앞서 언급한 sparse matrix 를 이용하는 방법이 데이터의 보관 및 연산을 위해서는 훨씬 효율적이지만, 설명의 편리성을 위해 이 포스트에서는 dict dict 로 표현하겠습니다. 아래는 위 그림을 Python 으로 표현한 것입니다. g[‘교대’][‘사당’] = 7.0 은 교대에서 사당을 갈 수 있고, 그 거리는 7.0 이라는 의미입니다. 반대로 g[‘사당’][‘교대’] = 7.0 이기도 합니다. 양방향으로 이동할 수 있으며, 양방향의 거리가 동일합니다.
이처럼 양방향의 거리가 동일하고 양방향으로 모두 이동가능할 경우에는 위 그림처럼 화살표를 표시하지 않기도 합니다. 이를 Undirected graph 라 합니다. 그리고 어떤 마디, 에 대하여 에서 로 갈 수 있는데, 그 역은 성립하지 않거나, 와 의 비용이 다른 경우를 Directed graph 라 합니다.
g = {'교대': {'동대문운동장': 34.0, '사당': 7.0, '충무로': 18.0},
'동대문운동장': {'교대': 34.0, '을지로3가': 3.0, '충무로': 2.0},
'사당': {'교대': 7.0, '서울역': 16.0, '신도림': 17.0},
'서울역': {'사당': 16.0, '시청': 2.0, '신도림': 17.0, '충무로': 5.0},
'시청': {'서울역': 2.0, '신도림': 23.0, '을지로3가': 4.0},
'신도림': {'사당': 17.0, '서울역': 17.0, '시청': 23.0},
'을지로3가': {'동대문운동장': 3.0, '시청': 4.0, '충무로': 1.0},
'충무로': {'교대': 18.0, '동대문운동장': 2.0, '서울역': 5.0, '을지로3가': 1.0}}이 그래프 안의 마디들, 마디 개수, 호의 개수를 파악합니다. 마디는 g 의 keys 뿐 아니라, g 의 values 의 keys 까지 합쳐서 살펴보아야 합니다. 물론 g 는 undirected graph 이기 때문에 g 의 keys 만 살펴보아도 됩니다. 하지만 directed graph 에서는 출발지의 후보들과 도착지의 후보들이 다를 수 있기 때문에 안전하게 아래와 같은 코드를 작성하여 마디들을 파악합니다.
출발지의 마디들을 nodes 로 만든 뒤, 도착지의 마디들의 set 을 nodes 에 업데이트합니다.
nodes = {source for source in g}
nodes.update({dest for destinations in g.values() for dest in destinations})
print(nodes)
# {'을지로3가', '충무로', '서울역', '동대문운동장', '사당', '신도림', '시청', '교대'}Nodes 와 edges 의 개수를 확인합니다. Nodes 의 개수는 len(nodes) 를 통하여 쉽게 구할 수 있습니다. Edges 의 개수는 g 의 values() 인 각 dict 의 크기의 합과 같습니다. 이 그래프는 8 개의 역에 대한 26 개의 edges 로 구성되었습니다.
n_nodes = len(nodes)
n_edges = sum((len(destinations) for destinations in g.values()))
print('n_nodes = {}, n_edges = {}'.format(n_nodes, n_edges))
# n_nodes = 8, n_edges = 26Ford algorithm
Ford algorithm 은 매우 간단합니다. 목적지까지 가는 길에 조금 더 가까운 경로를 발견한다면, 내가 알고 있는 최단 경로를 그 경로로 계속하여 대체합니다. 더 이상 대체할 경로가 없다면 현재 알고 있는 경로가 최단 경로가 됩니다. 우리는 ‘시청’에서 ‘사당’으로 가는 최단 경로를 찾아볼 것입니다.
Initialization
이를 위하여 Ford algorithm 의 초기화를 합니다. 출발지와 목적지가 주어지면, 출발지의 거리를 0 으로 설정합니다. 그리고 그 외의 모든 마디의 거리를 무한대로 설정합니다. 아직 어떤 마디까지도 가보지 않았기 때문에 실제로 얼마의 거리가 걸리는지를 알지 못한다는 의미입니다.
그러나 마디의 비용을 무한대로 설정할 필요는 없습니다. 한 역을 여러 번 방문하며 뱅글뱅글 돌지 않는 이상 (cyclic graph 가 아닌 이상) 가장 비용이 비싼 (거리가 먼) edge 의 weight 에 마디의 개수를 곱한 값보다 경로의 비용이 비쌀 수 없습니다. 그리고 weight 가 0 보다 큰 경우에는 한 마디를 여러 번 방문할수록 비용만 증가할 뿐입니다. 그렇다면 두 마디 사이의 경로에는 그래프 전체 마디 개수 - 2 개의 마디가 최대로 위치할 수 있습니다. 모든 지하철 역을 다 밟고서야 도착지에 도착하는 것과 같습니다.
그렇기 때문에 계산의 편의성을 위하여 무한대의 비용 대신 edge weight 의 최대값에 마디의 개수를 곱한 값을 이용합니다. 안전하게 edge weight 에 1 도 더했습니다.
max_cost = max(w for nw in g.values() for w in nw.values())
init_cost = n_nodes * (max_cost + 1)
print('max_cost = {}, init_cost = {}'.format(max_cost, init_cost))
# max_cost = 34.0 init_cost = 280.0‘시청’역을 기준으로 거리를 초기화합니다.
def initialize(start):
cost = {node:(0 if node == start else init_cost) for node in nodes}
return cost
cost = initialize('시청')시청 역 외의 모든 마디의 거리 비용은 280.0 으로 설정되었습니다. 이제 를 마디 까지의 비용으로, 를 에서 로 이동하는 비용인 edge weight 로 기술하겠습니다.
{'교대': 280.0,
'동대문운동장': 280.0,
'사당': 280.0,
'서울역': 280.0,
'시청': 0,
'신도림': 280.0,
'을지로3가': 280.0,
'충무로': 280.0}
Update rule
이제 모든 마디에 대해서 아래와 같은 조건이 만족하는 마디가 있는지 확인합니다. 우리가 확인할 조건은 아래와 같습니다.
if , then update
예시를 들어보면, 시청에서 서울역으로 가는 거리, 임을 알고 있습니다. 그런데 현재 입니다. 그러므로 을 으로 업데이트 합니다. 이는 내가 알고 있는 서울역까지 가는 경로 중 가장 짧은 경로의 비용이 2.0 이라는 의미입니다. 그리고 이는 다른 역까지의 거리는 모르겠지만, 적어도 시청에서 서울역까지 가는 거리 만큼은 현재 알려진 길보다 더 빠른 길을 찾았다는 의미입니다.
이 조건을 만족하는, 즉 더 빠른 길을 찾지 못할 때 까지 이 과정을 반복합니다. 만약 위 If 조건을 만족하는 경우가 없다면, 이를 알려줘야 합니다. changed 라는 변수를 두어 이를 표시합니다.
def update(cost):
changed = False
for from_, to_weight in g.items():
for to_, weight in to_weight.items():
if cost[to_] > cost[from_] + weight:
before = cost[to_]
after = cost[from_] + weight
cost[to_] = after
changed = True
return cost, changed한 번 update 함수를 거친 뒤 cost 의 변화입니다.
cost, changed = update(cost){'교대': 23.0,
'동대문운동장': 7.0,
'사당': 40.0,
'서울역': 2.0,
'시청': 0,
'신도림': 23.0,
'을지로3가': 4.0,
'충무로': 5.0}
Init cost 의 비용을 지니는 마디들이 없습니다. 사실 이건 운이 좋았기 때문입니다. ‘시청’에 인접한 역까지의 거리가 업데이트 되고, 그 역에서 출발하여 도달할 수 있는 다른 역까지의 거리도 단 한 번의 for loop 에서 수정되었기 때문입니다.
어떤 순서로 거리 비용이 업데이트 되는지 확인하기 위하여 위 코드에 한 줄을 추가하였습니다.
def update(cost):
changed = False
for from_, to_weight in g.items():
for to_, weight in to_weight.items():
if cost[to_] > cost[from_] + weight:
before = cost[to_]
after = cost[from_] + weight
cost[to_] = after
changed = True
print('{} -> {} : {} -> {}'.format(from_, to_, before, after))
return cost, changed다시 비용을 초기화한 뒤, 한 번의 update 함수를 거칩니다.
cost = initialize('시청')
cost, changed = update(cost)시청역에 인접한 ‘서울역, 신도림, 을지로3가’ 까지의 거리가 업데이트 되고, ‘신도림, ‘을지로3가’에서 출발하여 도달할 수 있는 ‘사당, ‘동대문운동장, 충무로’가 업데이트, ‘충무로’에서 출발하여 도달할 수 있는 ‘교대’까지의 거리가 모두 업데이트 되었습니다.
시청 -> 서울역 : 280.0 -> 2.0
시청 -> 신도림 : 280.0 -> 23.0
시청 -> 을지로3가 : 280.0 -> 4.0
신도림 -> 사당 : 280.0 -> 40.0
을지로3가 -> 동대문운동장 : 280.0 -> 7.0
을지로3가 -> 충무로 : 280.0 -> 5.0
충무로 -> 교대 : 280.0 -> 23.0
Worst case
그런데 언제나 위처럼 운이 좋은 것은 아닙니다. 언제나 최악으로 운이 좋지 않을 때도 대비를 해야 합니다. Worst case 는 알고리즘이 가장 많은 횟수로 If 부분을 확인하는 경우입니다. 그런데 Ford algorithm 은 위 If 문을 최대 마디 개수 과 호의 개수 의 곱 만큼만, 즉 만큼만 확인하면 된다고 알려져 있습니다.
이에 대한 이유는 매우 간단합니다. 아래 그림의 그래프에서 start 로부터 dest 까지의 최단 경로를 찾아봅니다.
그런데, 위 If 문을 아래의 순서대로 확인합니다. If 문을 만족하는 경우는 맨 마지막 경우입니다. 그래프의 모든 edge 를 확인하여 하나의 마디에 대한 거리가 업데이트 되었습니다. 즉 마디 2 까지의 최단 경로를 찾았습니다.
C[4] + w(4,dest) < C[dest]
C[3] + w(3,4) < C[4]
C[2] + w(2,3) < C[3]
C[source] + w(source,2) < C[2]
위 과정을 한 번 더 반복한다면 그 다음에는 마디 3에 대한 경로 비용이 업데이트 됩니다. 즉 모든 호를 살펴보는 행위를 마디의 개수만큼 하게 됩니다.
우리는 혹시 모를 무한 loop 를 방지하기 위하여 while loop 대신 for loop 을 이용하여 Update rule 을 구현합니다.
Iteratation
Worst case 분석으로부터 최대 반복 횟수를 설정하고, changed 가 False 이면 early stop 을 하는 과정을 넣어 ford 함수를 구현합니다.
def ford(start, destination):
cost = initialize(start)
for _ in range(n_nodes):
cost, changed = update(cost)
if not changed:
break
return cost‘시청’에서 ‘사당’까지의 거리입니다.
ford('시청', '사당')['사당']
# 18.0그리고 거리가 업데이트 되는 순서는 아래와 같습니다. 물론 운이 좋으면 더 빠르게 업데이트를 할 수도 있습니다.
시청 -> 서울역 : 280.0 -> 2.0
시청 -> 신도림 : 280.0 -> 23.0
시청 -> 을지로3가 : 280.0 -> 4.0
신도림 -> 사당 : 280.0 -> 40.0
을지로3가 -> 동대문운동장 : 280.0 -> 7.0
을지로3가 -> 충무로 : 280.0 -> 5.0
충무로 -> 교대 : 280.0 -> 23.0
교대 -> 사당 : 40.0 -> 30.0
서울역 -> 사당 : 30.0 -> 18.0
서울역 -> 신도림 : 23.0 -> 19.0
임의의 순서로 If 문을 확인하는 것보다 더 효율적인 방법들은 많습니다만, 이에 대해서는 이 포스트에서 다루지 않습니다.
Path finder
최단 경로는 시작점으로부터 조건을 만족하는 마디들을 이어가면 됩니다. 경로가 여러 개 일 수 있으니 list 로 최단 경로를 저장할 변수 mature 를 준비합니다.
immatures 는 아직 목적지에 도달하지 못한 중간 경로들입니다. 아래 코드는 최적화된 코드가 아닙니다. 쉬운 설명을 위한 예시일 뿐입니다.
def path_finder(start, dest, cost):
immatures = [[start]]
mature = []
for _ in range(n_nodes):
immatures_ = []
for path in immatures:
last = path[-1]
for adjacent, c in g[last].items():
if cost[adjacent] == cost[last] + c:
if adjacent == dest:
mature.append([p for p in path] + [adjacent])
else:
immatures_.append([p for p in path] + [adjacent])
immatures = immatures_
return mature
path_finder('시청', '사당', cost)
# [['시청', '신도림', '사당']]Related post
다음 포스트에서는 Ford algorithm 을 이용한 간단한 품사 판별기에 대하여 알아봅니다. 그리고 First order Hidden Markov Model 의 해는 Ford algorithm 을 이용한 최단 경로의 해와 같은 이유에 대해서도 알아봅니다.