Lloyd k-means 는 initial points 가 제대로 설정된다면 빠르고 안정적인 수렴을 보입니다. Lloyd k-means 의 입장에서 최악의 initial points 는 비슷한 점이 뽑히는 경우입니다. 이를 방지하기 위하여 다양한 initializer 가 제안되었으며, 그 중 널리 이용되는 것 중 하나가 k-means++ 입니다. 하지만, 데이터의 특성에 따라서는 k-means++ 가 제대로 작동하지 않을 수 있습니다. 이번 포스트에서는 어떤 경우에 k-means++ 가 잘 작동하지 않는지 그 이유를 살펴보고, 이를 해결하기 위한 방법에 대해서도 논의합니다.
k-means Introduction
k-means 는 다른 군집화 알고리즘과 비교하여 매우 적은 계산 비용을 요구하면서도 안정적인 성능을 보입니다. 그렇기 때문에 큰 규모의 데이터 군집화에 적합합니다. 문서 군집화의 경우에는 문서의 개수가 수만건에서 수천만건 정도 되는 경우가 많기 때문에 다른 알고리즘보다도 k-means 가 더 많이 선호됩니다. k-partition problem 은 데이터를 k 개의 겹치지 않은 부분데이터 (partition)로 분할하는 문제 입니다. 이 때 나뉘어지는 k 개의 partiton 에 대하여, “같은 partition 에 속한 데이터 간에는 서로 비슷하며, 서로 다른 partition 에 속한 데이터 간에는 이질적”이도록 만드는 것이 군집화라 생각할 수 있습니다. k-means problem 은 각 군집 (partition)의 평균 벡터와 각 군집에 속한 데이터 간의 거리 제곱의 합 (분산, variance)이 최소가 되는 partition 을 찾는 문제입니다.
우리가 흔히 말하는 k-means 알고리즘은 Lloyd 에 의하여 제안되었습니다. 이는 다음의 순서로 이뤄져 있습니다.
- k 개의 군집 대표 벡터 (centroids) 를 데이터의 임의의 k 개의 점으로 선택합니다.
- 모든 점에 대하여 가장 가까운 centroid 를 찾아 cluster label 을 부여하고,
- 같은 cluster label 을 지닌 데이터들의 평균 벡터를 구하여 centroid 를 업데이트 합니다.
- Step 2 - 3 의 과정을 label 의 변화가 없을때까지 반복합니다.
Lloyd k-means 는 대체로 빠르고 안정적인 학습 결과를 보여줍니다만, 몇 가지 단점을 가지고 있습니다. 이들은 우리가 데이터에 (Lloyd) k-means 를 적용할 때 의사결정을 해야 하는 부분이기도 합니다.
(1) initial points 설정
(2) iteration 횟수
(3) distance measure
(4) 적절한 k 의 개수 설정
(5) 학습된 클러스터의 레이블 부여
이번 포스트에서는 (1) initial points 설정에 대하여 다뤄봅니다.
k-means++
약 150 만 개의 문서집합을 k=1,000 의 k-means 로 학습 할 일이 있었습니다. scikit-learn 의 k-means 를 이용하려 하였지만, 10 시간이 지나도 initialize 단계가 끝나지 않았습니다 (verbose=True 로 설정하면 initialize 와 iteration 단계가 출력됩니다). 무엇인가 문제가 있다는 생각을 하였고, initializer 를 뜯어보게 되었습니다.
k-means 는 initial points 가 제대로 설정되지 않으면 불안정한 군집화 결과를 학습한다고 알려져 있습니다. 사실 k-means 의 학습 결과가 좋지 않는 경우는 initial points 로 비슷한 점들이 여러 개 선택 된 경우입니다. 이 경우만 아니라면 k-means 는 빠른 수렴속도와 안정적인 성능을 보여줍니다. 그렇기 때문에 질 좋은 (널리 퍼져있는, 서로 거리가 먼 initial points 를 선택하려는 연구들이 진행되었습니다. 그 중에서도 가장 널리 알려진 방법이 k-means++ 입니다 (scalable k-means^2 은 Spark 와 같은 분산 환경 버전의 k-means++ 입니다).
Python 의 scikit-learn 의 k-means 에는 사용자가 결정할 수 있는 다양한 options 이 있습니다. 이 중에서 init=’k-means++’ 이라는 부분이 보입니다. init 은 k-means++ 외에도 사용자가 임의로 설정한 seed points 혹은 random sampling 을 이용한 선택도 가능합니다.
def k_means(X, n_clusters, init='k-means++', precompute_distances='auto',
n_init=10, max_iter=300, verbose=False,
tol=1e-4, random_state=None, copy_x=True, n_jobs=1,
algorithm="auto", return_n_iter=False):k-means++ 은 다음의 과정으로 이뤄져 있습니다.
- 첫 initial point 은 임의로 선택합니다.
- 이후의 initial point 는 이전에 선택한 과의 거리인 가 큰 점이 높은 확률로 선택되도록 샘플링 확률 분포를 처럼 조절합니다. 이 분포에 따라 하나의 점을 선택합니다.
- k 개의 initial points 를 선택할 때까지 step 2 를 반복합니다.
Step 2 의 확률 덕분에 은 이전에 선택한 점 과 거리가 먼 점일 가능성이 높습니다. 이전 점들과 멀리 떨어진 점들이 선택되다보면 자연스레 서로 떨어진 점들이 선택될 것이라는 점이 k-means++ 의 아이디어 입니다.
그러나 k-means++ 가 잘 작동하지 않는 환경이 있습니다. Cosine 을 이용하는 문서 군집화 과정을 살펴봅시다. 문서 간 거리는 Euclidean distance 보다 Cosine distance 가 더 적합합니다. Bag of words model 을 이용한다면 문서가 sparse vector 로 표현되기 때문에 공통된 단어의 개수에 대한 정보를 포함하는 Jaccard, Cosine 과 같은 metrics 이 적합합니다^3. 샘플데이터는 3만여건의 하루 치 뉴스를 Bag of words model 로 표현한 데이터입니다. 9,774 개의 단어로 표현된 문서 집합입니다. 우리는 샘플데이터를 이용하여 문서 간 거리의 분포를 살펴봅니다.
print(x.shape)
#(30091, 9774)모든 문서 간 거리를 계산하면 오래 걸리기 때문에 1,000 개의 문서만 random sampling 하여 다른 문서 간의 거리를 계산합니다.
from sklearn.metrics import pairwise_distances
from numpy.random import permutation
from numpy import histogram
sample_idx = permutation(x.shape[0])[:1000]
dist = pairwise_distances(x, x[sample_idx,:], metric='cosine')
hist, bin_edges = histogram(dist, bins=20)문서 간 거리 분포는 0.85 이상인 경우가 91.79 % 에 해당합니다. 이는 고차원 벡터에서의 거리 척도의 특징입니다. 고차원에서는 Euclidean 이던지, Cosine 이던지 “가까운 거리는 의미가 있으나, 먼 거리는 의미가 없습니다”. 이에 대해서는 나중에 더 자세히 이야기하겠습니다. 결국, 대부분의 문서 간 거리가 0.85 ~ 1.00 이라는 의미이고, k-means++ 의 step 2 과정에서 계산된 sampling probability 는 사실 uniform distribution 에 가깝습니다. 그런데, 모든 점들 간의 거리를 계산하고, 이를 cumulative distribution 으로 바꾸어 random sampling 을 수행하는 과정은 생각보다도 많은 계산이 필요합니다. 즉 문서 군집화 과정에서 k-means++ 을 이용한다는 것은 “매우 비싼 random sampling” 을 수행하는 것입니다.
[distance range]: num of dist (%)
-------------------------------------------
[0.000 ~ 0.050] : 37848 (0.13 %)
[0.050 ~ 0.100] : 8106 (0.03 %)
[0.100 ~ 0.150] : 18554 (0.06 %)
[0.150 ~ 0.200] : 32180 (0.11 %)
[0.200 ~ 0.250] : 21512 (0.07 %)
[0.250 ~ 0.300] : 69913 (0.23 %)
[0.300 ~ 0.350] : 26691 (0.09 %)
[0.350 ~ 0.400] : 25581 (0.09 %)
[0.400 ~ 0.450] : 31954 (0.11 %)
[0.450 ~ 0.500] : 29859 (0.10 %)
[0.500 ~ 0.550] : 54503 (0.18 %)
[0.550 ~ 0.600] : 60503 (0.20 %)
[0.600 ~ 0.650] : 71768 (0.24 %)
[0.650 ~ 0.700] : 132200 (0.44 %)
[0.700 ~ 0.750] : 239247 (0.80 %)
[0.750 ~ 0.800] : 511296 (1.70 %)
[0.800 ~ 0.850] : 1098302 (3.65 %)
[0.850 ~ 0.900] : 2469531 (8.21 %)
[0.900 ~ 0.950] : 7754535 (25.77 %)
[0.950 ~ 1.000] : 17396917 (57.81 %)
k-means++ 은 한 가지 단점이 더 있습니다. Initial point 를 선택하기 위하여 이전에 선택한 만을 고려하면 는 와 비슷한 점일 수도 있습니다. 비슷한 점들을 선택하지 않는다는 보장을 하기 어렵습니다.
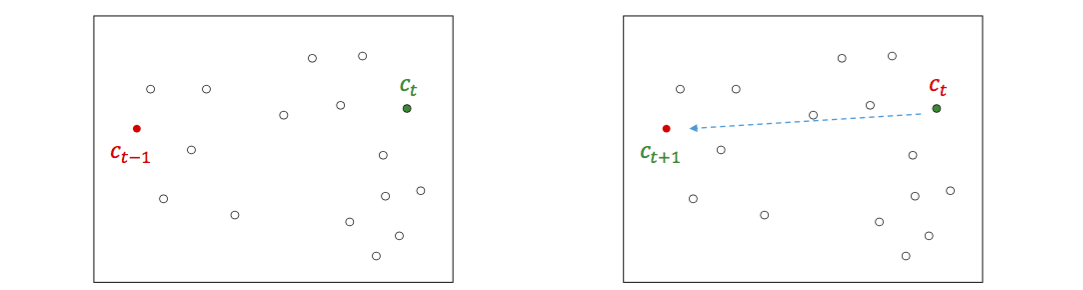
정리하면 pairwise distance distribution 이 uniform distribution 에 가까울 경우에는 k-means++ 은 무의미하고 비싼 계산을 수행하는 것입니다.
Ball cut. One of solutions
이를 해결하는 한 가지 방법입니다. 특히 user - content history 나 Bag of words model 과 같이 pairwise distribution 이 uniform distribution 에 가까울 때 효과적인 방법입니다. 대부분의 pairwise distance 가 최대값 (Non-negative vector 간의 Cosine distance 의 최대값은 1)에 가깝다면 점들 간 거리는 uniform distribution 에 가깝습니다. 이 때에는 비슷한 점들만 제외를 하여도 충분히 멀리 떨어진 (dispersed) 점들을 initial points 로 선택할 수 있다는 성질을 이용할 것입니다.
- 전체데이터 에서 개의 점들을 임의로 선택하여 을 만듭니다.
- 에서 한 개의 점 를 임의로 선택한 뒤, 와의 거리가 t 이하인 점들을 에서 제거합니다.
- 이 공집합이 아니며, k 개의 점을 선택할 때 까지 step 2 를 반복합니다.
- 만약 k 개의 점을 선택하지 못하였다면, - 에서 나머지 점들을 random sampling 합니다.
이는 아래 그림과 같은 효과를 가져옵니다. 에서 선택하는 점들은 적어도 거리가 t 이상인 점들로 구성이 됩니다. 그리고 위의 표와 같이 대부분의 거리가 최대에 가깝다면 를 2 ~ 5 정도로 선택하여도 가 공집합이 되는 일은 잘 일어나지 않습니다. 최악의 경우가 발생할 가능성이 k-means++ 보다 많이 줄어드는 것이죠.
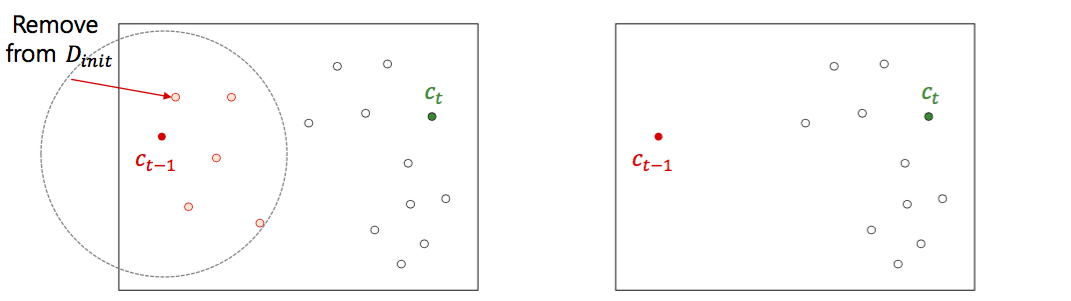
더하여 계산도 빠릅니다. 우리가 1M 의 데이터에 대하여 k=1,000 으로 k-means 를 학습할 경우, k-means++ 은 , 의 거리 계산을 합니다. k-means++ 의 실제 비용은 거리 계산에 cumulative distribution function 에서의 random sampling 비용을 더해야 합니다. 다시 한 번 강조하지만, 이 계산으로 얻는 결과는 random sampling 과 비슷합니다. 하지만 위에서 제안한 방법은 번의 계산만으로도 잘 퍼져있는 initial points 를 선택할 수 있습니다. 라면 번의 계산만으로도 충분합니다.
Performance
제안된 방법이 얼마나 효율적인지에 테스트를 수행하였습니다. 실험에 이용한 데이터는 122M 개의 문서로 이뤄진 IMDB reviews 입니다. 이 데이터에 대하여 100 개의 initial points 를 선택하였습니다.
| Dataset name | Num of docs | Num of terms | Num of nonzero | Sparsity |
|---|---|---|---|---|
| IMDB reviews | 1,228,348 | 68,049 | 181,411,713 | 0.9978 |
제안된 방법은 를 크게 잡을수록 조금씩 느려지긴 합니다만, 데이터의 개수가 k 보다 매우 클 경우에는 사실 상관도 없습니다. k-means++ 을 이용했을 때는 430 초 가까이 걸리는 계산이 제안된 방법을 이용하면 1초도 걸리지 않습니다.
| Alpha | Second | Faster (times) |
|---|---|---|
| 1.5 | 0.1915 | x 2253.45 |
| 3 | 0.2414 | x 1787.64 |
| 5 | 0.3124 | x 1381.36 |
| 10 | 0.4978 | x 866.89 |
| k-means++ | 431.5358 | x 1 |
사실 이 결과도 random sampling 과 비슷합니다. Initial points 간의 pairwise distance 를 계산하면 대부분 최대값에 가깝에 나타납니다. 심지어 random sampling 을 해도 그렇습니다. 만약 비슷한 점이 2 ~ 3 개 나타났다면 정말 적은 확률의 사건이 발생한거죠. 운명이에요.
애초에 널리 떨어진 점들에서 random sampling 을 하면 널리 떨어진 점들밖에 선택되지 않습니다만, 우리가 원하는 것은 비슷한 점들이 initial points 로 선택되지 않는 최소한의 (값싼) 안정장치 입니다. 그런 측면에서 제안된 방법은 계산 비용이 압도적으로 적으면서도 질 좋은 initial points 를 충분히 선택할 수 있습니다.
Packages
이와 관련된 코드는 github 의 clustering4docs repository 에 올려뒀습니다.
Reference
- Arthur, D., & Vassilvitskii, S. (2007, January). k-means++: The advantages of careful seeding. In Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms (pp. 1027-1035). Society for Industrial and Applied Mathematics.
- Bahmani, B., Moseley, B., Vattani, A., Kumar, R., & Vassilvitskii, S. (2012). Scalable k-means++. Proceedings of the VLDB Endowment, 5(7), 622-633.
- Huang, A. (2008, April). Similarity measures for text document clustering. In Proceedings of the sixth new zealand computer science research student conference (NZCSRSC2008), Christchurch, New Zealand (pp. 49-56).