Logitsic regression and Softmax regression for document classification

Logistic regression 은 binary classification 에 널리 이용되는 방법입니다. 이에 대한 기하학적인 의미를 알아봅니다. 또한 클래스가 3 개 이상일 경우의 일반화된 logistic regression 인 Softmax regression 으로 의미를 확장해봅니다. Softmax regression 을 이해하면 Word2Vec 과 같은 word embedding, representation learning 의 원리를 이해할 수 있습니다.

Geometric interpretation of logistic regression

Logsitic regression 은 머신러닝, 데이터마이닝 공부를 시작할 때 가장 먼저 만나는 classifier 입니다. Logistic 은 $(X, Y)$ 가 주어졌을 때, feature $X$ 와 $Y$ 와의 관계를 학습합니다. 특히 $Y$ 가 positive / negative 와 같이 두 개의 클래스로 이뤄져 있을 때 이용하는 방법입니다. Logistic regression 은 하나의 row, 혹은 벡터 공간의 하나의 점 $x$ 가 주어졌을 때, 클래스가 $y$ 일 확률을 학습한다고도 이야기합니다. exponential 의 범위는 $(0, +\infty)$ 이기 때문에 $\frac{1}{1 + exp(-\theta^Tx)}$ 는 $(0, 1)$ 의 범위를 지닙니다. 그래서 확률로 해석을 할 수 있습니다.

$$y_{\theta}(x) = \frac{1}{1 + exp(-\theta^Tx)}$$

위 식을 조금 더 자세하게 풀어보면 positive, negative 클래스에 속할 확률을 각각 계산할 수 있습니다. exponential 의 값은 nonnegative 이기 때문에 모든 경우에 대하여 $exp(\theta_i^Tx)$ 의 값을 더하여, 이 값으로 각각의 $exp(\theta_i^Tx)$ 를 나눠주면 확률 형식이 됩니다.

$$\begin{bmatrix} P(y=pos~\vert~x) \\ P(y=neg~\vert~x) \end{bmatrix} = \begin{bmatrix} \frac{exp(-\theta_1^Tx)}{exp(-\theta_1^Tx) + exp(-\theta_2^Tx)} \\ \frac{exp(-\theta_2^Tx)}{exp(-\theta_1^Tx) + exp(-\theta_2^Tx)} \end{bmatrix}$$

여기서 $\frac{exp(\theta_1^Tx)}{exp(\theta_1^Tx) + exp(\theta_2^Tx)}$ 의 분자, 분모를 $exp(\theta_1^Tx)$ 로 나눠주면 $\frac{1}{1 + exp(-\theta^Tx)}$ 이 됩니다. positive 일 확률을 계산하였고, 확률의 총합은 1 이기 때문에 negative 는 따로 계산하지 않아도 되는 것입니다.

혹은 logistic regression 을 기하학적으로 해석하기도 합니다. Bias 를 포함한 logistic regression 의 단면 (hyperplane) 은 빨간색과 파란색의 점들을 구분하는 결정단면 (separating hyperplane) 입니다. 쉽게 말해 경계면을 학습하는 것입니다. 이 결정단면의 수식은 $(\theta^Tx)$ 입니다. 즉, 단면 위에 있는 점은 positive, negative 클래스에 속할 확률이 각각 0.5 라는 의미입니다. 어느 쪽에 속하는지 확신할 수 없으니까요.

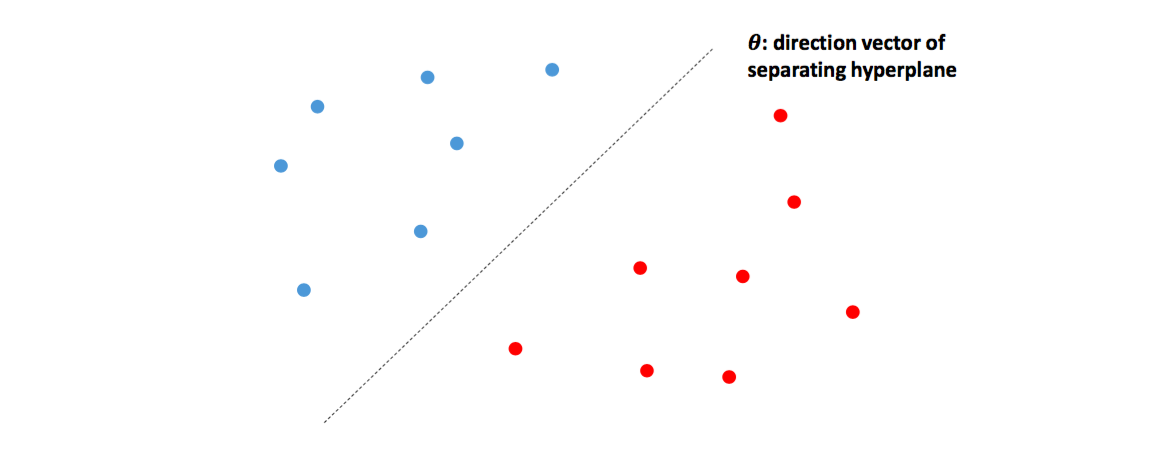
그럼 위에서 pos, neg 의 확률을 각각 계산하는 형식으로 logistic regression 을 표현할 때도 기하학적으로 해석해봅시다. 각각의 $\theta$ 는 일종의 클래스의 대표벡터가 됩니다. $\theta_1$ 은 파란색 점들을 대표하는 백터, $\theta_2$ 는 빨간색 점들을 대표하는 벡터입니다. 하나의 클래스 당 하나의 대표벡터를 가집니다 (단 하나의 대표벡터를 지니기 때문에 linear inseparable case 가 생깁니다. 이는 Feed-forward neural network 에서 이야기하겠습니다). 만약 한 점 $x$ 가 $\theta_1$ 과 일치한다면 $exp(\theta_1^Tx)$ 는 어느 정도 큰 양수가, $exp(\theta_2^Tx)$ 는 0에 가까운 값이 되기 때문에 $x$ 의 클래스 1에 해당할 확률이 1이 됩니다. Logistic regression 은 각 점에 대하여 각 클래스의 대표벡터에 얼마나 가까운지를 학습하는 것입니다.

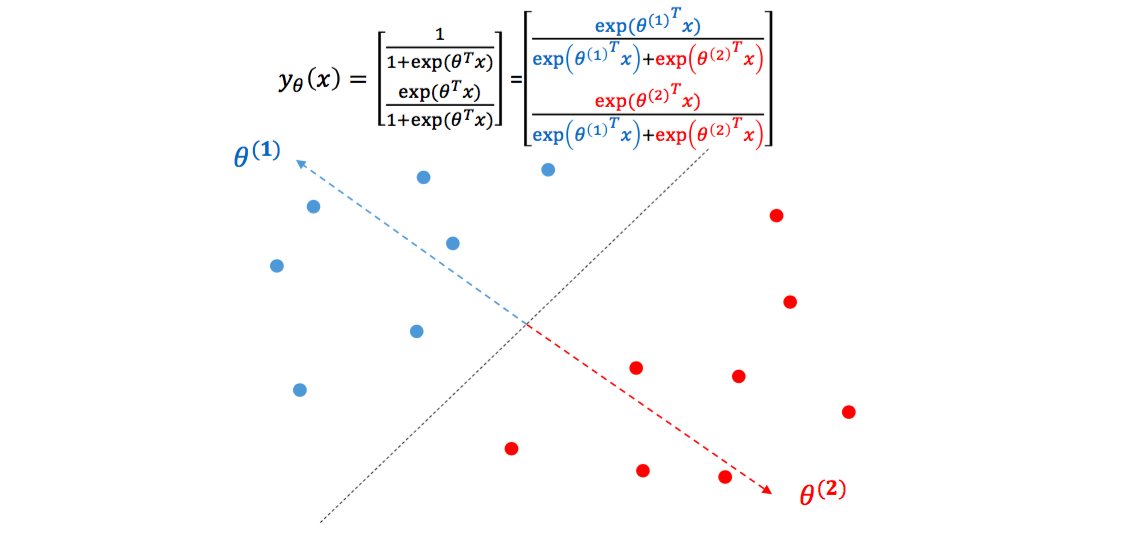
Meaning of coefficients in document classification

$\theta$ 는 logistic regression 의 coefficient vector 입니다. $\theta_{kj}$ 는 feature j 가 클래스 k 의 기여도로 해석하기도 합니다. 우리는 뉴스 문서 집합에서 ‘연예뉴스’와 그 외 뉴스를 구분하는 문서판별기를 logistic regression 으로 학습합니다. Coefficient 는 ‘연예뉴스’ 클래스에 대하여 각 단어 (feature)가 얼마나 기여를 하는지를 나타냅니다. ‘보였다, 이었다’와 같은 단어는 어느 클래스에서도 등장하는 문법 기능의 단어들입니다. 좋은 판별기라면 이런 단어들은 무시가 될 것입니다. ‘외교, 정책, 무역’ 과 같은 단어는 연예뉴스보다는 정치, 외교, 경제 뉴스에서 더 많이 등장했을 것입니다. 이런 단어들이 등장한다면 연예뉴스가 아니라는 힌트를 얻을 수 있습니다. 하지만 ‘무대, 공연, 가수’와 같은 단어들이 등장한다면 연예뉴스라는 힌트를 얻게 되는 것입니다. Bag of words model (term frequency vector) 로 표현된 $x$ 는 coefficient vector 와 내적이 되기 때문에 각 단어가 등장한 횟수만큼 coefficient 가 더해집니다. 그리고 exponential 을 통하여 $(-\infty, +\infty)$ 인 값이 $(0, +\infty)$ 로 변환됩니다.

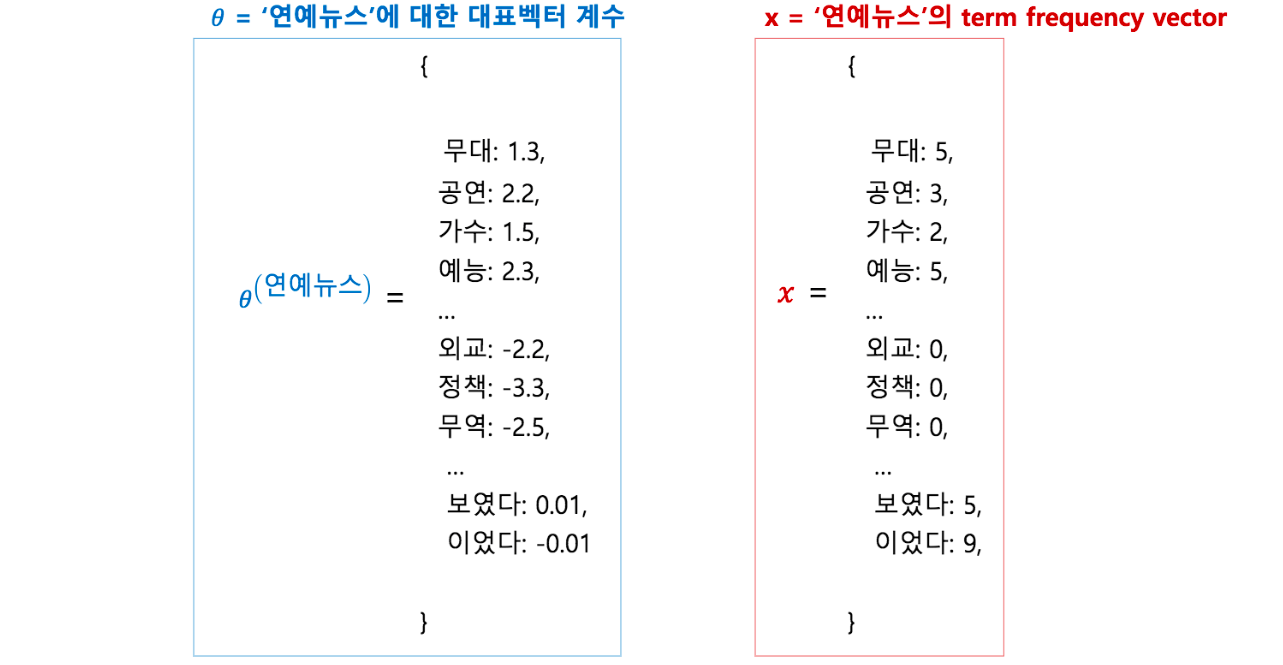
각 클래스에서 유독 자주 등장하는 단어들이 큰 coefficient 를 지닐 것이고, 이런 단어들이 등장하면 해당 클래스의 문서라고 판단하는 것입니다.

Softmax regression

여기까지 정리가 되었다면 softmax regression 은 한 가지만 더 생각하면 됩니다. 클래스가 2 개가 아닌 n 개라면, 총 n 개의 대표벡터를 학습하는 것입니다. 각 클래스를 구분하는 결정단면은 대표벡터의 Voronoi diagram 과 같습니다. 단, 각 대표벡터에 얼마나 가까운지는 벡터 간 내적 (inner product) 로 정의됩니다. 한마디로, $x$ 에 대하여 내적이 가장 큰 대표벡터의 클래스로 $y$ 를 판단하는 것입니다. 마치 1-NN classifier 처럼 말이죠.

$$\begin{bmatrix} P(y=1~\vert~x) \\ \cdots \\ P(y=n~\vert~x) \end{bmatrix} = \begin{bmatrix} \frac{exp(\theta_1^Tx)}{\sum_k exp(\theta_k^Tx)} \\ \cdots \\ \frac{exp(\theta_n^Tx)}{\sum_k exp(\theta_k^Tx)} \end{bmatrix}$$

우리는 인공데이터를 만들어서 softmax regression 의 특징을 좀 더 살펴보겠습니다. 데이터 생성 파일은 링크로 올려두었습니다. 총 5 개의 클래스에 대하여 각 클래스 별로 100 개의 2 차원 데이터를 만들었습니다. 방사형으로 퍼진 형태입니다. X 는 데이터, Y 는 각 데이터의 클래스입니다.

X, Y = generate_spherical(n_class=5, n_per_class=100, dimension=2)

이를 matplotlib 을 이용하여 scatter plot 을 그려봅니다. 만약 Jupyter notebook 에서 작업중이시라면 %matplotlib inline 을 꼭 적어주세요.

%matplotlib inline
import matplotlib.pyplot as plt

plt.scatter(X[:,0], X[:,1], s=2, c=Y)
plt.show()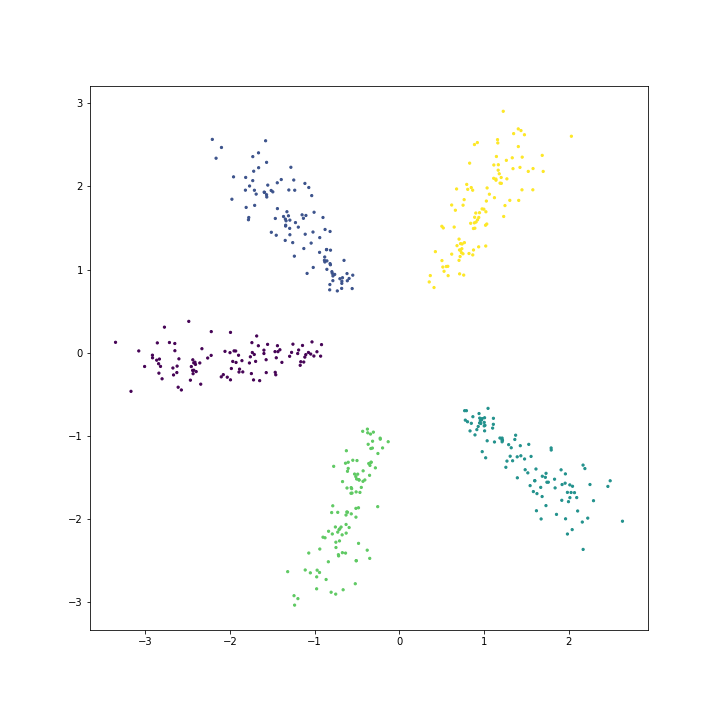

Scikit-learn 에서 logistic / softmax regression 은 모두 sklearn.linear_model.LogisticRegression 에 구현되어 있습니다. Y 의 값의 종류가 3 개 이상이면 softmax regression 을 학습힙니다.

from sklearn.linear_model import LogisticRegression

logistic = LogisticRegression()
logistic.fit(X, Y)

Coefficients 는 LogisticRegression.coef_ 에 저장되어 있습니다. 앞선 설명대로라면 coefficient 는 각 클래스의 대표벡터여야 합니다. 5 개의 클래스에 대한 2차원 방향벡터가 학습됩니다. coef 의 row 는 클래스의 대표벡터입니다.

coef = logistic.coef_
print(coef.shape) # (5,2)

이를 위 데이터 scatter plot 에 함께 겹쳐 그립니다. 대표벡터는 star marker 를 이용합니다.

plt.scatter(X[:,0], X[:,1], s=2, c=Y)
plt.scatter(coef[:,0], coef[:,1], s=100, c=class_colors, marker='*')
plt.show()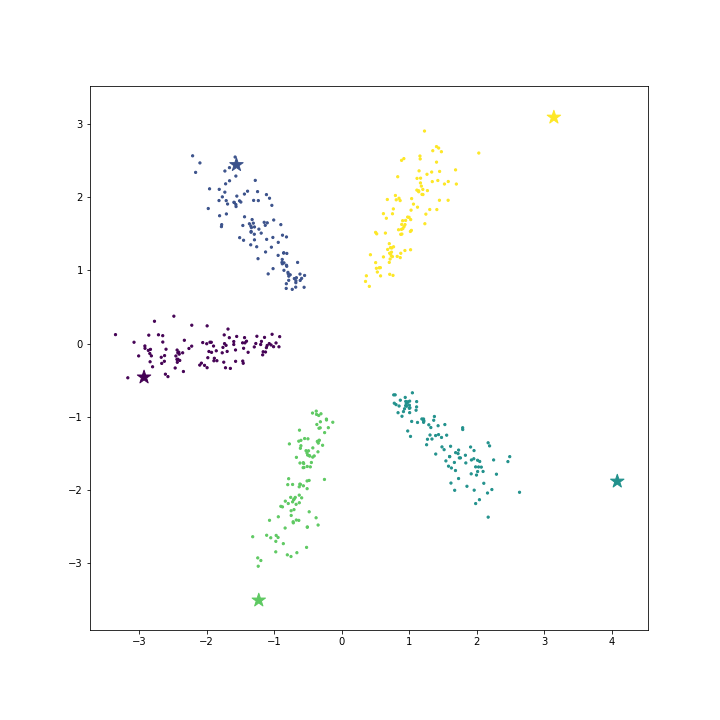

각 클래스의 데이터가 서로 다른 방향으로 골고루 펼쳐져 있기 때문에 클래스의 대표벡터들이 각 클래스의 분포와 비슷하게 잘 퍼져있습니다. 하지만 데이터가 아래의 그림처럼 전체 공간의 한쪽에만 몰려 있다면, 방향벡터가 각 클래스의 데이터와 같은 방향인 것은 아닙니다. 데이터 분포의 경계에 있는 두 클래스의 대표벡터는 빈 공간에 위치합니다. 이는 softmax regression 에 데이터가 입력될 때 대표벡터와의 내적의 상대적인 크기가 더 중요하기 때문입니다. 대표벡터들은 널리 퍼져있어야 (서로 다른 방향벡터를 가져야) 각 클래스에 속할 확률이 확연히 다르게 나타나기 때문에 이처럼 학습됩니다.

Read more

우리는 아직 정규화 (regularization)에 대하여 이야기하지 않았습니다. L1, L2 regularization 을 이용하여 모델을 해석이 용이하게 만들기도 하고, 과적합 (over-fitting)을 방지하기도 합니다. 이에 대해서는 다음 포스트에서 알아봅니다.