Logistic regression with L1, L2 regularization and keyword extraction

Logistic regression 은 feature X 와 클래스 Y 간의 관계인 클래스의 대표벡터를 coefficients 에 학습합니다. 대표벡터 (coefficient) 를 구성하는 값 $\alpha_{kj}$ 들은 j 번째 feature, $X_j$ 와 클래스 k 와의 상관성입니다. 때로는 coefficients vector 가 sparse vector 가 되도록 유도함으로써 classification 에 중요한 몇 개의 features 만을 이용하도록 강제할 수 있습니다. 이를 L1 regularization 혹은 LASSO model 이라 부릅니다. LASSO 는 feature selection 의 역할을 합니다. 그리고 이를 응용하여 keyword extraction 을 할 수 있습니다.

Review of logistic regression

Softmax (Logistic) regression 은 각 클래스 별 대표벡터를 학습합니다. 그림은 5 개의 클래스의 데이터입니다. 그리고 star marker 는 각 클래스의 대표벡터입니다. 학습된 classifier 는 새로운 $x$ 가 입력되었을 때 대표벡터들과의 내적 기준으로 가장 가까운 클래스로 $x$ 의 레이블을 판별합니다.

$\begin{bmatrix} P(y=1~\vert~x) \\ \cdots \\ P(y=n~\vert~x) \end{bmatrix} = \begin{bmatrix} \frac{exp(\theta_1^Tx)}{\sum_k exp(\theta_k^Tx)} \\ \cdots \\ \frac{exp(\theta_n^Tx)}{\sum_k exp(\theta_k^Tx)} \end{bmatrix}$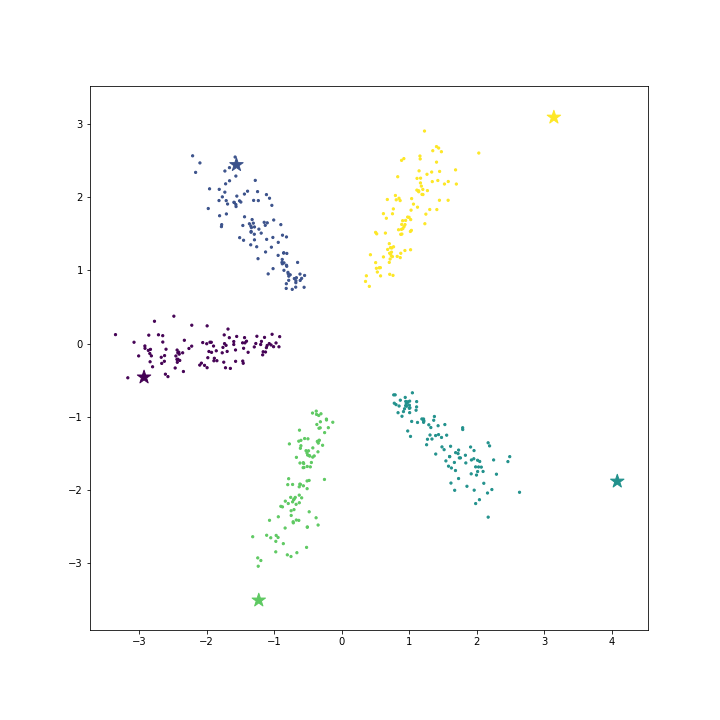

Logistic regression with L2 regularization

Regularization 은 학습되는 대표벡터의 크기와 모양을 조절합니다 (크기를 조절하다보면 모양도 따라 변할 수 있습니다). L2 regularization 은 각 대표벡터의 크기를 조절합니다. L2 norm 은 벡터의 Euclidean 크기입니다. 예를 들어 $(3, 4)$ 의 2차원 벡터는 $\sqrt{3^2 + 4^2} = 5$ 입니다. 그래고 아래의 cost 는 학습된 모델의 비용이며, 머신러닝 알고리즘은 이 비용을 줄이는 방향으로 모델 (coefficient)을 학습합니다. Logistic regression 의 입장에서는 대표벡터가 학습할 모델입니다. 그리고 비용은 주어진 $x$ 로 $y$ 를 얼마나 잘 예측하는지에 대한 비용 (error)와 학습된 모델의 norm 의 합으로 이뤄져 있습니다. 아래 식의 $\lambda \rVert \theta \rVert_2$ 는 logistic regression 이 학습하는 coefficient vector 의 L2 norm 입니다. 간단히 말하여 대표벡터들의 L2 norm 의 합이라 생각해도 좋습니다. L2 regularization 을 이용하는 logistic regression 은 이 대표벡터의 크기를 줄이는 방향으로 학습을 유도합니다. 그리고 이를 Ridge regression 이라고도 부릅니다.

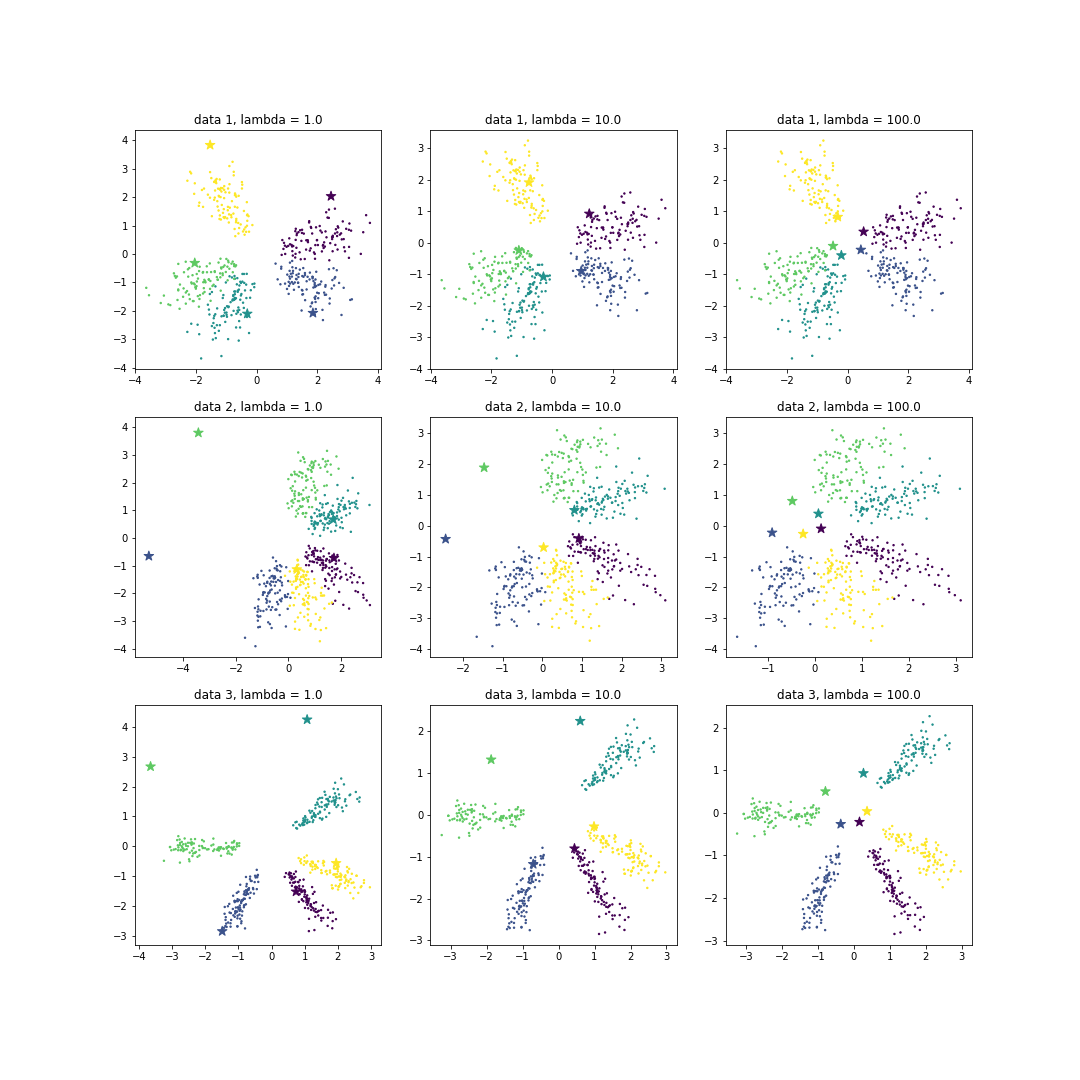
$cost = \sum_{i}^{n} \left(y_i - \frac{1}{1 + exp(-\theta^Tx)} \right) + \lambda \rVert \theta \rVert_2$

아래 그림의 data 1 의 경우, L2 regularization 비용계수인 $\lambda$ 가 커질수록 대표벡터의 크기가 줄어듭니다. 대표벡터가 원점 근처로 모여듭니다. 하지만 방향성은 유지가 되고 있습니다. 방향성이 바뀌면 해당 클래스를 대표하지 않기 때문입니다. 좀 더 재밌는 결과는 data 2 나 3 과 같이 각 클래스의 데이터가 골고루 펼쳐져 있지 않는 경우입니다. $\lambda$ 가 작을 때에는 대표벡터와 각 클래스의 데이터들이 다른 공간에 위치합니다. 각 클래스에 속할 확률만 잘 계산되면 되기 때문입니다. 일종의 과적합 (overfitting) 입니다. 하지만 regularization cost 가 커질수록 대표벡터들은 원점에 모여들고, 각 클래스를 좀 더 잘 표현하는 모양으로 학습됩니다. Regularization 은 overfitting 을 해결하는 수단입니다.

이보다 overfitting 과 regularization 의 관계를 잘 설명하는 예시는 유명한 regression 예시입니다. 아래 그림은 Wikipedia 의 regularization page 의 그림입니다. 녹색 선은 regularization 비용이 큰 경우, 파란 선은 비용이 작은 경우 입니다. 좋은 모델은 학습데이터에 대해서 y 를 잘 맞추기만 하면 되는 것은 아닙니다. 모델이 간략하여 학습데이터가 없는 부분에서도 잘 틀리지 않을 수 있어야 합니다. 이를 일반화 성능이 좋다고 이야기합니다. Regularization 은 모델을 복잡하지 않게 만들어 일반화 성능을 높이는 역할을 합니다.

Logistic regression with L1 regularization

L1 regularization 은 조금 특별합니다. 그전에 L1 norm 에 대하여 알아봅니다. L1 norm 은 벡터의 각 요소들의 절대값의 합입니다. $(3, -4)$ 의 L1 norm 은 $\vert 3 \vert + \vert -4 \vert = 7$ 입니다. 수학적인 설명은 하지 않지만, L1 norm 은 딱히 도움이 되지 않는 features 의 coefficient 를 0 으로 학습하도록 유도합니다. 그래서 L1 regularization 을 feature selection 의 수단으로 이용하기도 합니다. Coefficient 가 0 인 feature 는 그 값이 얼마여도 대표벡터와의 내적에 영향을 주지 않기 때문입니다.

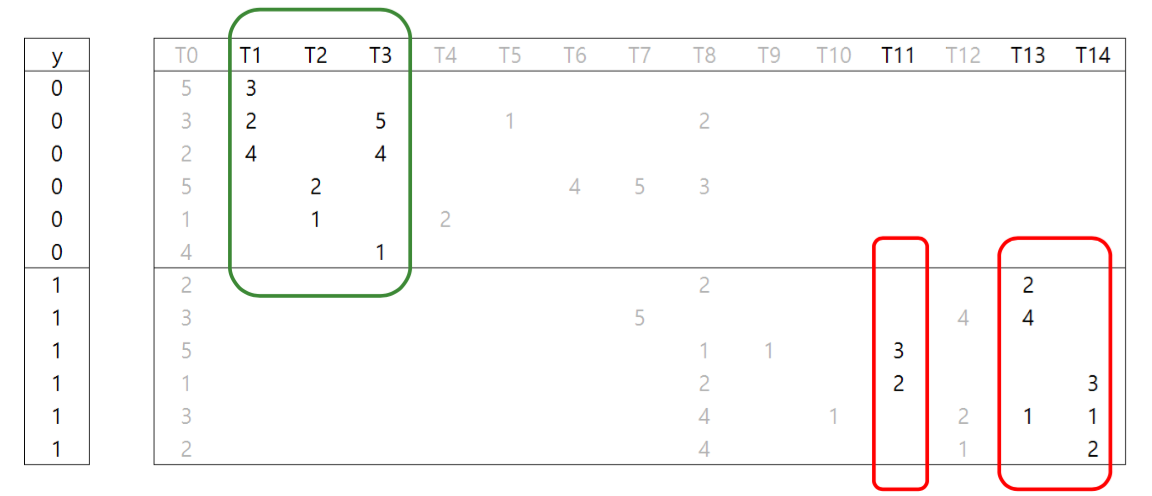
$cost = \sum_{i}^{n} \left(y_i - \frac{1}{1 + exp(-\theta^Tx)} \right) + \lambda \rVert \theta \rVert_1$

아래의 그림은 0 과 1 두 가지 클래스를 구분하기 위하여 T0 ~ T14 까지 15 개의 단어 (features) 를 이용하는 문서판별기의 예시입니다. T0 는 0 과 1 모두에서 자주 등장하므로 0 과 1 을 구분하는 힌트가 되지 않습니다. T0 은 버립시다. T4 나 T6 이 등장하면 클래스가 0 이라는 아주 명확한 힌트가 됩니다만, 이 두 개의 features 를 모두 이용하느니 T2 한 개만 이용해도 됩니다. 그리고 T6 과 T7 은 중복된 재료입니다. 만약 반드시 T6 을 이용한다면 T7 은 이용할 필요가 없습니다. 이런 논리로 생각하면 [T1, T2, T3, T11, T13, T14] 은 문서 판별을 잘 수행하는 최소한의 feature set 입니다. 이들만 coefficient 가 0 이 아니면 됩니다. 그리고 L1 regularization 을 이용하는 logistic regression 은 바로 이렇게 행동합니다. 중복되지 않는 최소한의 유용한 features 를 선택합니다. 물론 L1 regularization 은 이런 논리로 coefficients 를 학습하지는 않지만, 그 결과는 이와 같습니다.

그리고 L1 norm 을 이용하는 logistic regression 을 LASSO regression 이라 부릅니다. Least Absolute Shrinkage and Selection Operator 의 약어입니다.

Keyword extraction

키워드 추출이란 말은 매우 익숙한 말입니다. 하지만 키워드 추출은 매우 모호한 말입니다. 키워드의 정의는 분석의 목적이나 데이터의 특징에 따라 다릅니다. 그렇기 때문에 키워드 추출은 키워드에 대한 정의부터 시작해야 합니다. 한 문서에 많이 등장한 단어를 키워드로 정의하는 것은 매우 위험합니다. ‘-은, -는, -이, -가’와 같은 조사는 모든 문서에서 가장 많이 등장할 단어들입니다. 그보다는 어떤 문서집합을 연상시킬 수 있는 몇 개의 단어를 키워드로 정의하면 더 좋을 것 같습니다. 어떤 문서집합을 연상시키려면 해당 단어가 그 문서집합에서만 유독 많이 등장하여야 할 것입니다. 그렇다면 lasso 는 이 목적을 위한 적절한 머신러닝 알고리즘입니다. 문서집합을 구분할 수 있는 단어 중에서, 해당 문서집합에만 유독 자주 나오던 단어들을 선택할 것입니다. 더하여 그 중에서도 correlation 이 높은, 중복된 단어집합 에서는 하나의 단어만 선택하여주니 최소한의 단어 셋을 찾기에 유용합니다.

실험에 이용할 데이터셋은 2016-10-20 의 뉴스기사입니다. 뜬금없지만, 전 그룹 ‘아이오아이’를 좋아합니다. 이 시기는 ‘너무너무너무’ 곡을 발표했던 시기입니다. 그렇다면 ‘너무너무너무’는 ‘아이오아이’ 관련 기사의 키워드입니다. 그리고 음악방송 관련 단어들도 키워드로 선택될 것입니다. 한 번 확인해봅시다. 데이터셋의 크기는 (30091, 9774) 입니다. 1 만여개의 단어로 이뤄진 3 만여개의 문서집합입니다. 그리고 ‘아이오아이’ 단어의 id 는 5537 입니다.

print(X.shape) # (30091, 9774)
print(vocab2idx['아이오아이']) # 5537

‘아이오아이’를 포함한 문서들은 1, 그 외의 문서들은 0 의 레이블을 부여하고 이를 구분하는 핵심단어들을 선택하는 선택하는 lasso 모델을 만들겁니다. 단, ‘아이오아이’ 라는 단어는 데이터에서 제외하겠습니다. 두 문서를 구분할 수 있는 가장 명확한 힌트이기 때문입니다.

scipy.sparse 에서 제공하는 sparse matrix 를 효율적으로 다루는 방법은 아니지만, 가장 이해가 쉬운 방법으로 ‘아이오아이’ (idx=5537) 을 제거하겠습니다. sparse matrix 는 세 개의 list 로 이뤄져 있다고 생각할 수 있습니다 (사실은 더 많은 정보로 이뤄져있지만요). (i, j) = v 가 0 이 아닌 row, column, 그리고 이에 해당하는 data (v) 에 대한 세 가지 리스트로 이뤄져있습니다. X.nonzero() 를 통하여 row, column lists 를 가져옵니다. 그리고 (i, j, value) 에 대하여 j 가 5537 (아이오아이)이 아닐 때만 list 에 append 합니다. 그 뒤 다시 csr_matrix 로 이를 묶었습니다.

from scipy.sparse import csr_matrix

rows, cols = X.nonzero()
data = X.data

# Create X_. tf matrix that dosen't have term '아이오아이'
rows_, cols_, data_ = [], [], []
for r, c, d in zip(rows, cols, data):
    if c == 5537:
        continue
    rows_.append(r)
    cols_.append(c)
    data_.append(d)
X_ = csr_matrix((data_, (rows_, cols_)))

이제 ‘아이오아이’를 포함한 문서를 찾아보겠습니다. 먼저 이 단어의 column vector 를 만듭니다. 그 뒤, nonzero elements 의 row idx 를 가져오면 됩니다. 그리고 이를 이용하여 Y 를 만들었습니다. 물론 이것이 가장 효율적인 방법은 분명 아닙니다. 효율적인 방법은 sparse matrix handling 에서 논의합니다.

# Create Y. 1 if a doc has '아이오아이' term else 0
pos_set = set(X[:,5537].nonzero()[0]) 
Y = [1 if r in pos_set else 0 for r in range(X.shape[0])]

97 개의 문서에 ‘아이오아이’가 등장하였었기 때문에 X_ 의 nonzero elements 의 개수는 97 개가 줄었습니다.

print('number of positive docs = {}'.format(len(pos_set))) 
# number of positive docs = 97

print('nonzero elements: {} -> {}'.format(X.nnz, X_.nnz))
# nonzero elements: 1934111 -> 1934014

이제 logistic regression 을 만듭니다. penalty = ‘l1’ 으로 설정하면 lasso model 이 됩니다. Default 는 ‘l2’ 입니다. 학습된 coefficient 는 reshape(-1) 을 합니다. matrix 가 아닌 array 가 됩니다.

from sklearn.linear_model import LogisticRegression

logistic = LogisticRegression(penalty='l1')
logistic.fit(X_, Y)
coef = logistic.coef_.reshape(-1)

print(coef.shape) # (9774,)

enumerate() 를 이용하여 coef 를 (idx, weight) 로 만든 뒤, weight 기준으로 정렬을 합니다. Weight 가 0 이라면 사용하지 않는 단어이기 때문에 print for loop 을 멈춥니다.

for vocab_idx, w in sorted(enumerate(coef), key=lambda x:-x[1])[:100]:
    if w <= 0:
        break
    print(idx2vocab[vocab_idx], end=' ')

weight 의 크기가 0 보다 큰 상위 100 개의 키워드를 확인해봅니다. 가장 weight 가 큰 단어는 기대했던대로 ‘아이오아이’의 노래 제목 ‘너무너무너무’ 입니다. 그리고 ‘엠카운트다운, 무대, 프로그램’ 과 같은 음악방송 용어들, ‘다이아, 유정, 프로듀스101’ 과 같은 아이오아이 관련 단어들이 키워드로 선택된 것을 볼 수 있습니다.

너무너무너무 선의 산들 엠카운트다운 챔피언 사나 드림 뮤직 먹고 
완전체 일산 세련 같이 뉴스1스타 컴백 소속사 곡으로 보컬 열창 
만나게 인사 마무리 박진영 선보 무대 수출 서울신문 활동 다이아
유정 인기 매력 등장 카메라 개인 고양시 비타민 수준 멤버들 걸그룹 
한편 1위 예능 순위 세븐 발매 야구 불독 다비치 파워풀 이날 걸크러쉬
신용재 화려 프로듀스101 반전 일간스포츠 프로그램 스마트폰 트와이스 
키미 일산동구 프로듀스 기자 