벡터는 행렬로 표현할 수 있습니다. Distributed representation 처럼 벡터의 대부분의 값이 0 이 아닐 경우에는 numpy.ndarray 와 같은 double[][] 형식으로 벡터를 저장합니다. Row 는 각 entity, column 은 벡터 공간에서의 각 차원에 해당합니다. 이와 반대로 sparse matrix 는 벡터의 많은 값들이 0 입니다. 대부분의 값이 일정하다면 그 값이 아닌 다른 값들만을 메모리에 저장하면 메모리를 효율적으로 이용할 수 있습니다. 데이터를 저장할 때도 마찬가지입니다. Sparse matrix 는 이를 위한 format 입니다. Format 이 array 가 아닌기 때문에 이를 잘 이용하기 위한 방법을 알아야 합니다. Python 의 scipy.sparse 라이브러리에는 sparse matrix format 들이 구현되어 있습니다. 이에 대하여 이야기합니다.
Type of sparse matrix
Sparse matrix 는 데이터 분석에서 자주 접하는 형식입니다. Bag of words model 을 이용하여 표현되는 문서의 term frequency matrix 는 sparse format 입니다. 한 문서에 등장하는 단어의 종류는 전체 문서 집합의 단어 종류에 비하여 매우 작기 때문입니다. 추천 알고리즘이 이용하는 user - item purchase history matrix 역시 sparse format 입니다. 한 사용자가 구매하였던 items 의 숫자는 전체 아이템의 숫자에 비하여 매우 작습니다.
Sparsity 는 전체 벡터공간에서 0 인 값들의 비율입니다. 100 개의 문서에 1000 개의 단어가 등장하였고, 평균 10 개의 단어가 한 문서에 있었다면 sparsity 는 다음처럼 정의됩니다.
\[sparsity = \frac{990 \times 100}{100 \times 1000} = 1 - \frac{10 \times 100}{100 \times 1000} = 0.99\]Scipy 에서 제공하는 sparse matrix class 는 다양합니다. 우리는 이 중에서 coo, csc, csr, dok 에 대하여 이야기합니다.
- bsr_matrix : Block Sparse Row matrix
- coo_matrix : A sparse matrix in COOrdinate format.
- csc_matrix : Compressed Sparse Column matrix
- csr_matrix : Compressed Sparse Row matrix
- dia_matrix : Sparse matrix with DIAgonal storage
- dok_matrix : Dictionary Of Keys based sparse matrix.
- lil_matrix : Row-based linked list sparse matrix
Sample data
우리는 다음과 같은 4 x 5 의 행렬을 만들어 네 가지 sparse matrix type 에 대하여 알아봅니다.
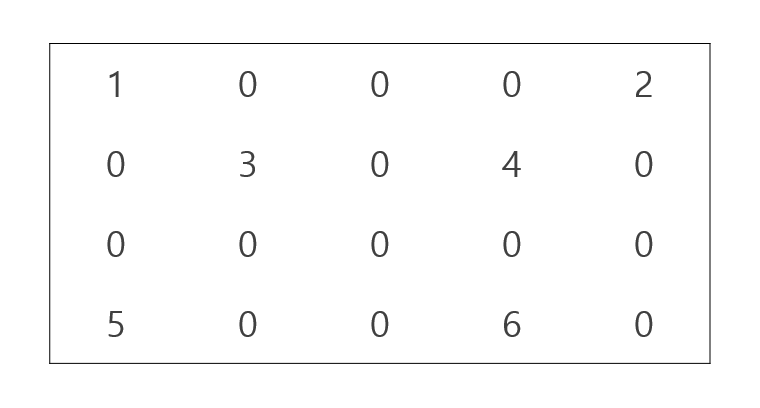
scipy.sparse 의 matrix 를 만드는 방법은 sparse martrix 의 구성요소를 직접 입력하는 방법과 numpy.ndarray 를 입력하는 방법이 있습니다. 후자는 튜토리얼처럼 연습할 때에만 쓸 수 있는 방법입니다. 애초에 numpy.ndarray 를 만들고 싶지 않는 경우에 sparse matrix 를 만드니까요.
import numpy as np
from scipy.sparse import csr_matrix
x = [[1, 0, 0, 0, 2],
[0, 3, 0, 4, 0],
[0, 0, 0, 0, 0],
[5, 0, 0, 6, 0]]
x = np.asarray(x)
csr = csr_matrix(x)혹은 sparse matrix 의 구성요소를 직접 입력할 수도 있습니다. 그 구성요소는 rows, columns, data 를 각각 분리하여 저장한 array (like) 입니다. 위의 matrix 는 다음처럼 만들 수 있습니다.
from scipy.sparse import csr_matrix
rows = [0, 0, 1, 1, 3, 3]
cols = [0, 4, 1, 3, 0, 3]
data = [1, 2, 3, 4, 5, 6]
csr = csr_matrix((data, (rows, cols)))sparse matrix 의 구성요소는 정확히는 (data, indices, indptr) 입니다. 하지만 이를 직접 만드는 것보다 (data, (rows, cols)) 를 만드는 것이 더 편하기 때문에 이 방법만 적어뒀습니다. 이 세 가지 구성요소에 대한 설명은 바로 다음에 적혀있습니다.
dense matrix 로 변환하여 모양을 확인하고 싶을 때에는 todense() 를 이용합니다. sparse matrix 가 numpy.ndarray 로 변환됩니다.
csr.todense()matrix([[1, 0, 0, 0, 2],
[0, 3, 0, 4, 0],
[0, 0, 0, 0, 0],
[5, 0, 0, 6, 0]], dtype=int64)
텍스트 데이터의 doc - term matrix 를 다룰 때에는 csr 나 csc matrix 를 자주 이용합니다. 여기에 dok 와 coo 에 대해서도 알아봅니다.
DoK format
Dictionary of Keys 의 약자입니다. 0 이 아닌 값들의 위치를 저장하는 방식으로 (row, column) 을 key 로 지니는 dict 로 구성되어 있습니다. 직관적인 구조이며 x[i,j] 에 접근하기가 쉽습니다. (i,j) pair 의 key 가 dict 에 존재하는지 확인하고, 그 값이 있다면 key 를 value 로 map 합니다. \(O(1)\) 의 access 비용이 듭니다. 새로운 값을 저장할 때에도 hash map 에 데이터를 넣는 것 뿐입니다.
numpy.ndarray 인 x 를 이용하여 dok matrix 를 만듭니다.
from scipy.sparse import dok_matrix
dok = dok_matrix(x)dok matrix 는 Python dict 처럼 key(), values(), items() 함수를 제공합니다. keys() 를 입력하면 list of tuple 형태로 저장된 key set 이 return 됩니다. (row, column) 의 list 입니다.
print(dok.keys())
# dict_keys([(0, 0), (0, 4), (1, 1), (1, 3), (3, 0), (3, 3)])values() 의 return 은 각 key 에 해당하는 value 입니다.
print(dok.values())
# dict_values([1, 2, 3, 4, 5, 6])items() 를 이용하여 for loop 을 만들 수도 있습니다.
for key, value in dok.items():
print('{} = {}'.format(key, value))
# (0, 0) = 1
# (0, 4) = 2
# (1, 1) = 3
# (1, 3) = 4
# (3, 0) = 5
# (3, 3) = 6행렬에서 nnz 는 number of nonzero 의 약자입니다. Sparsity 를 계산하는데 이용할 수 있습니다.
print(dok.nnz) # 6shape 은 행렬의 크기입니다. numpy.ndarray 와 scipy.sparse 에 모두 구현되어 있습니다.
print(dok.shape) # (4,5)이를 이용하여 sparsity 를 계산할 수 있습니다.
sparsity = 1 - dok.nnz / (dok.shape[0] * doc.shape[1])COO matrix
COO matrix 는 list of tuple 형식으로 0 이 아닌 값을 저장합니다. tuple 에는 (row, column, data) 인 (i, j, v) 가 저장됩니다. 내적이나 slicing 의 기능을 제공하지 않습니다. sparse.io.mmread 의 type 이기도 합니다. dok, csc, csr 형식으로 변환하기 위해서 todok(), tocsc(), tocsr() 을 이용합니다.
from scipy.io import mmread
coo = mmread('path')
csr = coo.tocsr()
csc = coo.tocsc()
dok = coo.todok()CSR matrix
Compressed Sparse Row 의 약자입니다. Row 순서대로 데이터를 저장합니다.
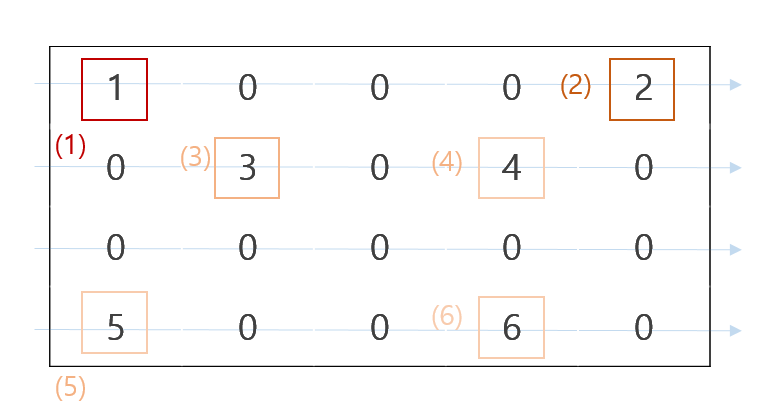
CSR matrix 에는 indices, indptr, data 가 있습니다. data 는 0 이 아닌 요소의 값 입니다.
print(csr.data) # [1 2 3 4 5 6]indices 는 data 의 값에 해당하는 column index 입니다.
print(csr.indices) # [0 4 1 3 0 3]indptr 은 row 별로 data 의 begin index 와 end index 가 저장되어 있습니다. 예를 들어 0 번째 row 의 data 는 data[0:2] 입니다. 또한 이에 해당하는 column index 는 indices[0:2] 입니다.
print(csr.indptr) # [0 2 4 4 6]그렇기 때문에 indptr 의 길이는 row 개수보다 한 개 더 많습니다.
# num of rows + 1
len(csr.indptr) # 5indptr 과 indices 를 이용하면 row 별 연산이 가능합니다. zip(indptr, indptr[1:]) 을 수행하면 (begin, end) index 를 얻을 수 있습니다. enumerate() 는 row indx 를 얻기 위하여 입력하였습니다.
for i, (b, e) in enumerate(zip(csr.indptr, csr.indptr[1:])):
for idx in range(b, e):
j = csr.indices[idx]
d = csr.data[idx]
print('({}, {}) = {}'.format(i, j, d))
# (0, 0) = 1
# (0, 4) = 2
# (1, 1) = 3
# (1, 3) = 4
# (3, 0) = 5
# (3, 3) = 6sparse.nonzero() 를 실행하면 rows, cols 가 return 됩니다.
rows, cols = csr.nonzero()CSC matrix
Compressed Sparse Cow 의 약자입니다. csr 과 반대로 column 순서대로 데이터를 저장합니다.
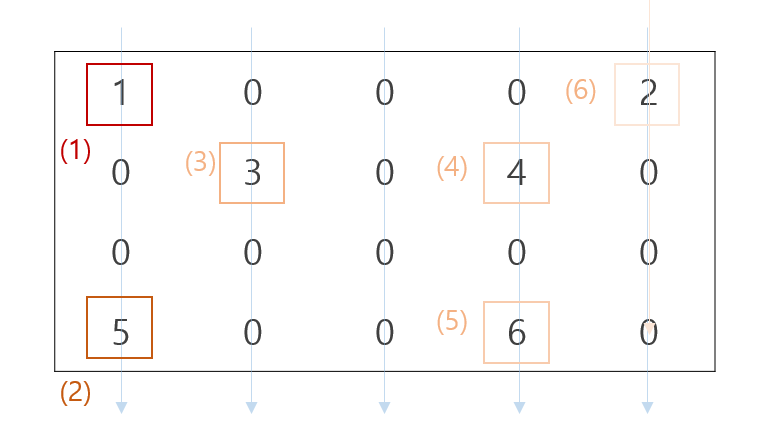
CSC matrix 에도 indices, indptr, data 가 있습니다. data 는 0 이 아닌 요소의 값 입니다. CSC matrix 는 column 순서로 데이터를 저장하기 때문에 csr.data 와 csc.data 는 순서가 다릅니다.
print(csr.data) # [1 2 3 4 5 6]
print(csc.data) # [1 5 3 4 6 2]indices 는 data 의 값의 row index 입니다.
print(csr.indices) # [0 4 1 3 0 3]
print(csc.indices) # [0 3 1 1 3 0]indptr 은 column 별로 data 의 row begin index 와 row end index 가 저장되어 있습니다. 예를 들어 0 번째 column 의 data 는 data[0:2] 에 저장되어 있습니다. 그리고 그 때의 column index 는 indices[0:2] 입니다.
print(csr.indptr) # [0 2 4 4 6]
print(csc.indptr) # [0 2 3 3 5 6]이번에는 indptr 의 길이가 column 개수보다 한 개 더 많습니다.
# num of column + 1
len(csc.indptr) # 6indptr 과 indices 를 이용하면 column 별 연산이 가능합니다.
for j, (b, e) in enumerate(zip(csc.indptr, csc.indptr[1:])):
for idx in range(b, e):
i = csc.indices[idx]
d = csc.data[idx]
print('({}, {}) = {}'.format(i, j, d))
# (0, 0) = 1
# (3, 0) = 5
# (1, 1) = 3
# (1, 3) = 4
# (3, 3) = 6
# (0, 4) = 2Sparse matrix I/O and Matrix Market format (mtx file)
scipy.io 를 이용하여 matrix 를 저장하고 읽을 수 있습니다. 어떤 형식의 matrix 를 mmwrite 로 저장하여도 그 형식은 matrix market 으로 같습니다.
from scipy.io import mmwrite
from scipy.io import mmread
mmwrite('mat.mtx', csr)Matrix market format 은 sparse matrix 의 텍스트 저장 방식입니다. 위의 3 줄은 header 입니다. 아래의 예시는 ‘mat.mtx’ 파일의 맨 앞 5 줄입니다. 첫 줄은 파일 형식을 정의하는 고유 head, 두번째 줄은 띄어쓰기 입니다. 3 번째 줄은 이 행렬의 num row, num column, nnz 입니다. 즉 nnz 는 네번째 줄부터의 line number 입니다. 파일의 총 line number 는 세번째줄 마지막 숫자 + 2 입니다.
네번째 줄부터 데이터가 저장됩니다. Row 와 column index 은 0 이 아닌 1 부터 시작됩니다. Python 스럽지는 않습니다. 왜 이런 포멧이 만들어졌는지는 찾아보지 못했지만, matlab 과 같은 소프트웨어들의 row, column index 가 1 부터 시작하는데, 이 때 만들어진 포멧이 아닐까 짐작하고 있습니다.
%%MatrixMarket matrix coordinate integer general
%
4 5 6
1 1 1
1 5 2
만약 직접 mmread 를 만든다면 다음처럼 만들 수 있습니다. data 는 int 외에도 float 가 될 수 있으므로 float casting 을 하였습니다. 파일을 메모리에 올리지 않고 line by line 으로 작업할 일이 있다면 이 함수를 base 로 이용할 수 있습니다.
from scipy.sparse import csr_matrix
def my_read(path):
with open(path) as f:
# skip head
for _ in range(3):
next(f)
rows = []
cols = []
data = []
for line in f:
elements = line.split()
i = int(elements[0])
j = int(elements[1])
d = float(elements[2])
rows.append(i)
cols.append(j)
data.append(d)
return csr_matrix((data, (rows, cols)))Efficient ways for handling sparse matrix
Sparse matrix 를 다룰 때 최대한 피해야 하는 작업들이 있습니다.
No slicing. Avoid to row/column-wise operation
첫째는 slicing 입니다. Row 나 column 단위로 작업을 하기 위하여 다음 같은 코드를 작성할 수도 있습니다.
for i in range(csr.shape[0]):
row = csr[i,:]
# ...slicing 을 하면 scipy.sparse 의 _get_submatrix() 함수가 실행됩니다. return 이 될 때 같은 종류의 class 를 하나 더 만듭니다. 매우 불필요한 계산을 합니다. 반드시 Python 에서 row / column 단위의 작업을 수행해야 한다면 indptr 와 indices 를 이용하는 방식으로 코드를 작성하는 것이 좋습니다.
class csr_matrix():
# ...
def _get_submatrix(self, row_slice, col_slice):
"""Return a submatrix of this matrix (new matrix is created)."""
def process_slice(sl, num):
# ...
return i0, i1
M,N = self.shape
i0, i1 = process_slice(row_slice, M)
j0, j1 = process_slice(col_slice, N)
indptr, indices, data = get_csr_submatrix(
M, N, self.indptr, self.indices, self.data, i0, i1, j0, j1)
shape = (i1 - i0, j1 - j0)
return self.__class__((data, indices, indptr), shape=shape,
dtype=self.dtype, copy=False)Do not assign 0 to entire row (or column)
특정 column 이나 row 의 모든 값을 0 으로 만들고 싶을 때, x[i,j] = 0 을 할당할 수 있습니다. Dense matrix 에서는 매우 자연스러운 방법이지만, sparse matrix 에서는 이 작업이 좋지 않습니다.
아래처럼 3 번째 column 의 모든 값에 0 을 할당하면, warning 까지 뜹니다.
csr_zero = csr.copy()
csr_zero[:,3] = 0SparseEfficiencyWarning: Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient. SparseEfficiencyWarning
csr.data 와 csr_zero.data 의 길이도 다릅니다. 0 인 (row, column) 은 값을 부여할 필요가 없는데 0 이 할당되었습니다.
print(len(csr_zero.data)) # 8
print(len(csr.data)) # 6
print(csr_zero.data) # array([1, 0, 2, 3, 0, 0, 5, 0], dtype=int64)더 좋은 방법은 다음처럼 0 을 할당하고 싶은 값을 제거하는 것입니다. 속도가 가장 빠른 방법은 아니지만 설명을 위한 직관적인 코드입니다. 해당 column 을 건너뛰는 새로운 rows, columns, data list 를 만들어 return 합니다. 이 때 반드시 shape 을 x.shape 으로 지정해야 합니다. 마지막 column 을 제거할 경우 return 되는 matrix 의 column 개수가 1 개 줄어들 수도 있기 때문입니다.
def remove_column(x, idx):
rows, cols = x.nonzero()
data = x.data
rows_, cols_, data_ = [], [], []
for r, c, d in zip(rows, cols, data):
if c == idx:
continue
rows_.append(r)
cols_.append(c)
data_.append(d)
return x.__class__((data_, (rows_, cols_)), shape=x.shape)Use distance functinon of numpy
sparse matrix 의 연산을 할 경우에는 최대한 numpy, scipy, scikit-learn 의 함수를 이용하는 것이 좋습니다. 내적을 위해서는 numpy.dot 을 이용할 수 있습니다. Distance 계산을 위해서는 sklearn.metric.pairwise_distances 를 이용할 수 있습니다.
numpy 와 scipy 는 c 로 만들어진 라이브러리입니다. 이들의 값을 Python 으로 불러들인 뒤, python 환경에서 작업을 수행하면 변수의 type check 를 거치게 됩니다. 이 비용이 꾀 큽니다. 가능한 numpy 와 같은 library 의 함수를 이용하여 작업을 한 뒤, 결과만 python 으로 받는 것이 좋습니다.
거리 계산을 위해 pairwise_distances 를, rows 나 column 간의 거리 계산 후 가장 가까운 row, column 을 찾기 위해서는 pairwise_distances_argmin 을 이용합니다. pairwise_distances(axis = ?) 을 이용하면 row, column 단위의 작업을 조절할 수 있습니다.
from sklearn.metrics import pairwise_distances
from sklearn.metrics import pairwise_distances_argmin