Graph ranking 은 nodes 와 edges 로 구성된 networks 에서 중요한 nodes 를 찾기 위한 방법입니다. 대표적인 알고리즘인 PageRank 는 Google 의 초기 검색 엔진에 이용된 알고리즘으로 유명합니다. PageRank 를 이용하여 web page graph 에서 중요한 pages 를 찾은 뒤, 검색 결과를 출력할 때 그들의 우선 순위를 높입니다. PageRank 는 그 외에도 recommender system 이나 natural language processing 분야에서도 자주 이용되었습니다. 이 포스트에서는 대표적인 graph ranking 알고리즘인 PageRank 와 HITS 에 대하여 알아봅니다.
Graph
그래프는 데이터를 표현하는 방식 중 하나입니다. 그래프는 마디 (node, vertex) 와 호 (edge) 로 이뤄져 있으며, \(G = (V, E)\) 로 자주 표현합니다.
아래의 그림처럼 인물 간 친밀도를 edge 로 표현하면 인맥(?) 그래프를 만들 수 있습니다. 마디는 각 인물입니다. 그래프 전체에서 마디의 종류가 하나이기 때문에 이 그래프를 homogeneous graph 라 합니다.

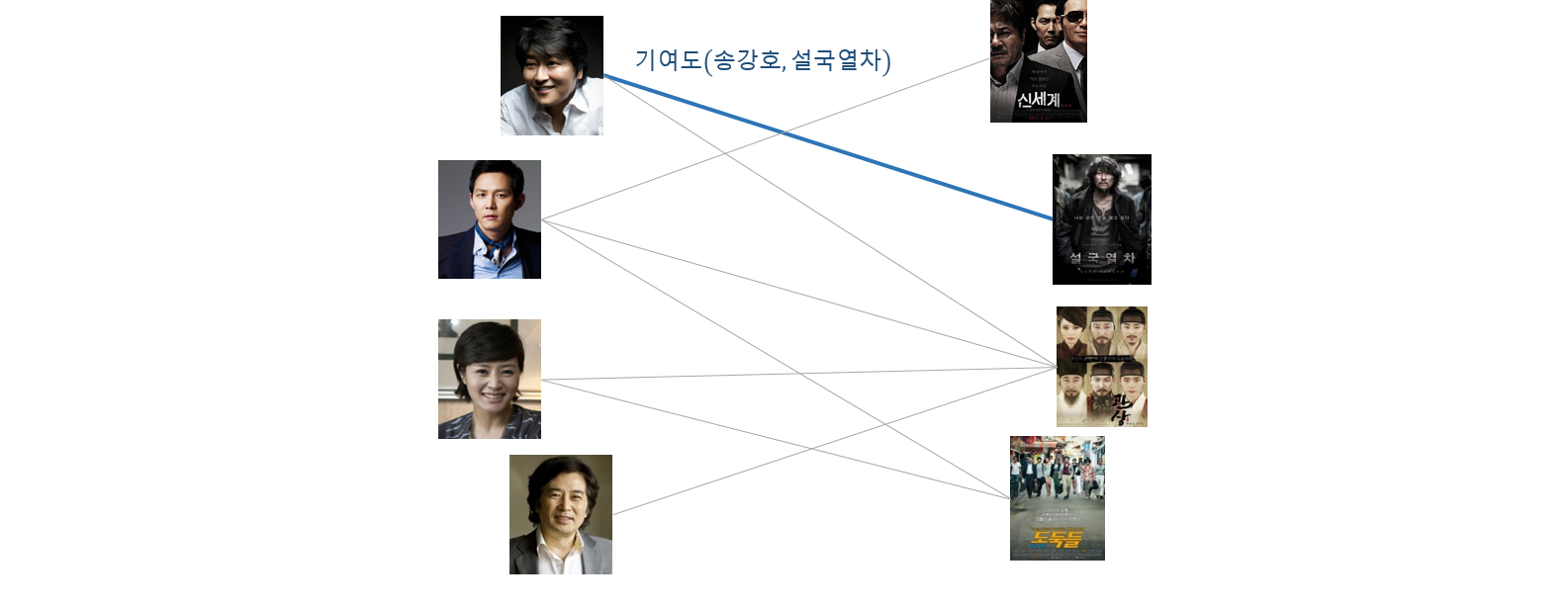
혹은 배우와 영화의 출연 관계를 그래프로 표현할 수도 있습니다. 각 배우의 각 영화에 대한 기여도를 edge 로 표현할 수도 있습니다. 배우 간에는 연결 관계가 없고, 영화 간에도 연결 관계가 없습니다. 오로직 배우와 영화 간에만 연결 관계가 있습니다. 이처럼 마디의 종류가 두 개로 분류되어 연결이 되는 그래프를 bipartite graph 라 합니다. 그리고 마디의 종류가 다르기 때문에 heterogeneous graph 로 분류합니다.
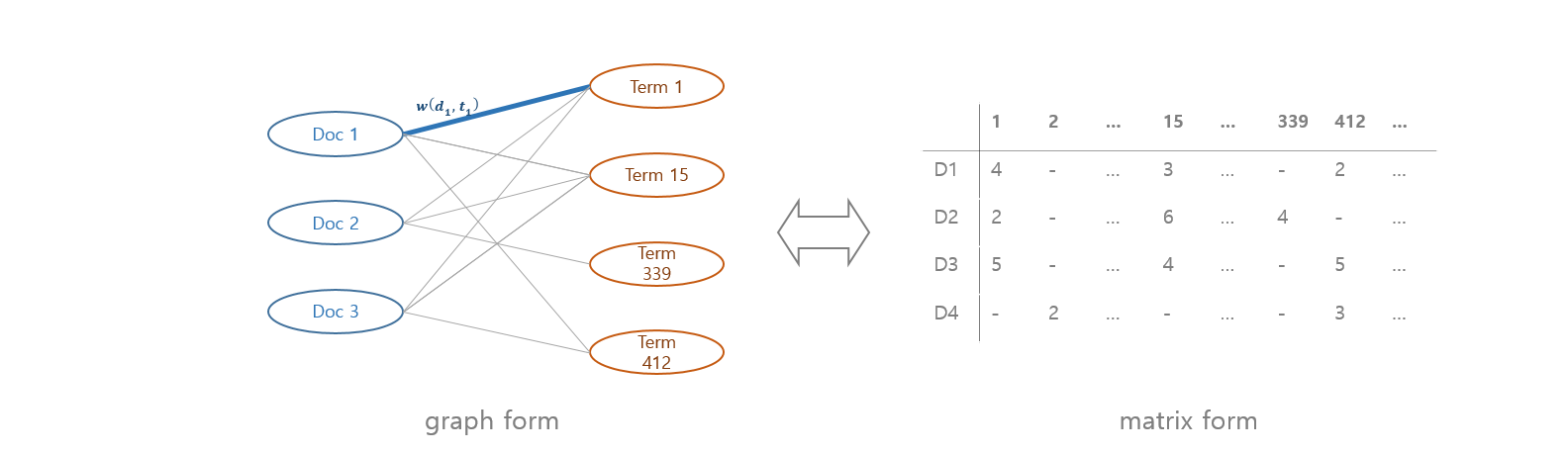
Graph 는 행렬 (matrix) 형식으로 표현될 수 있습니다. 100 개의 마디로 구성된 그래프라면 rows, columns 의 개수가 100 개인 \(100 \times 100\) 행렬로 표현할 수 있습니다. \(X[3,5] = 3\) 은 3 번 마디와 5 번 마디를 연결하는 호, edge 의 값이 3 이라는 의미입니다.
그래프는 벡터 공간보다 더 자유로운 표현이 가능합니다. 벡터 공간에서는 점 p1 과 p2 가 가깝고 p2 와 p3 가 가까우면 p1 과 p3 역시 가까울 가능성이 높습니다. 하지만 그래프에서는 edge 를 두 마디 간의 거리로 정의할 경우 아래처럼 p1 과 p3 을 매우 마디로 정의할 수도 있습니다. Metric space 가 아닌 데이터를 표현하기에 적합합니다.
e(p1, p2) = 1
e(p2, p3) = 1
e(p1, p3) = 100
Metric space 는 쉬운 표현으로, “거리가 정의되는 공간” 입니다. Metric space 는 points 와 distance 로 정의되며, 네 가지 성질이 만족해야 합니다. \(x, y\) 은 metric space 의 임의의 두 점입니다.
- \(d(x, y) \ge 0\) : 두 점 사이의 거리는 0 이거나 그보다 큽니다.
- \(d(x, y) = 0 \Leftrightarrow x = y\) : 거리가 0 이려면 두 점은 같아야 합니다.
- \(d(x, y) = d(y, x)\) : \(x\) 에서 \(y\) 로의 거리와 \(y\) 에서 \(x\) 로의 거리는 같습니다.
- \(d(x,z) \le d(x,y) + d(y,z)\) : 삼각부등식이 성립합니다.
다소 수학적인 이야기입니다만, 어려운 이야기는 아닙니다. 우리가 살고 있는 이 3 차원 세상이 metric space 이며, 4 번은 p1 과 p2 가 가깝고 p2 와 p3 이 가까우면 p1 과 p3 도 가깝다는 이야기입니다. 이런 공간에서 \(x\) 가 \(y\) 를 가깝다(친하다)고 생각하는데, \(y\)는 \(x\) 를 가깝지(친하지) 않다고 표현할 수 없습니다. 하지만 graph 는 이 표현이 가능합니다.
그렇기 때문에 graph 의 표현 형태가 행렬이라 하여, 이를 벡터 공간에 표현된 점이라 생각하면 안됩니다. 하지만 벡터 공간의 점들은 graph 로 표현이 가능합니다. 문서를 벡터로 표현할 때 자주 이용하는 term frequency matrix 는 문서와 단어로 이뤄진 bipartite graph 로 표현이 가능합니다.
Graph 는 벡터 공간보다 더 자유로운 표현이 가능합니다. 이러한 성질을 반영하여 graph 로 표현된 데이터에서 어떤 패턴을 찾아내려는 머신러닝 알고리즘들도 있습니다. 소셜 네트워크에서 소통이 원활히 이뤄지는 그룹인 community 를 찾기도 합니다. 특정 주제의 메시지가 소셜 네트워크에서 어떻게 확산되는지를 확인하기도 합니다. 혹은 분자 구조 그래프를 보고 분자의 특성이나 종류를 판별 (classification) 하기도 합니다. 혹은 중요한 마디를 선택하기도 합니다.
PageRank
Concept
PageRank 는 가장 대표적인 graph ranking 알고리즘입니다. Google 의 Larry Page 가 초기 Google 의 검색 엔진의 랭킹 알고리즘으로 만든 알고리즘으로도 유명합니다. Web page graph 에서 중요한 pages 를 찾아서 검색 결과의 re-ranking 의 과정에서 중요한 pages 의 ranking 을 올리는데 이용되었습니다.
중요한 web pages 를 찾기 위하여 PageRank 는 매우 직관적인 아이디어를 이용하였습니다. 많은 유입 링크 (backlinks)를 지니는 pages 가 중요한 pages 라 가정하였습니다. 일종의 ‘투표’입니다. 각 web page 가 다른 web page 에게 자신의 점수 중 일부를 부여합니다. 다른 web page 로부터의 링크 (backlinks) 가 많은 page 는 자신에게 모인 점수가 클 것입니다. 자신으로 유입되는 backlinks 가 적은 pages 는 다른 web pages 로부터 받은 점수가 적을 것입니다. 또한 모든 pages 가 같은 양의 점수를 가지는 것이 아닙니다. 중요한 pages 는 많은 점수를 가지고 있습니다. Backlinks 가 적은 링크라 하더라도 중요한 page 에서 투표를 받은 pages 는 중요한 page 가 됩니다.
이처럼 직관적인 아이디어가 PageRank 에서 갑자기 나타난 것은 아닙니다. Bibliometrics (계량서지학) 에서는 citations 에 대하여 연구하였습니다. Citations 이 많은 책은 중요한 책입니다. 그리고 그 책이 reference 로 이용하는 책 역시 중요할 책일 것입니다. PageRank 의 links 는 bibliometrics 에서의 citation 입니다. 실제로 PageRank 의 논문을 살펴보면 bibliometrics 의 논문들이 참고되어 있습니다. 그리고 이제 PageRank 는 information retrieval 외의 다양한 분야에서 응용되고 있습니다. 한 아이디어가 여러 학문 분야로 퍼져나갑니다.
Formular
PageRank 에서 각 node 의 중요도 \(PR(u)\) 는 다음처럼 계산됩니다. \(B_u\)는 page \(u\) 의 backlinks 의 출발점 마디입니다. \(v\) 에서 \(u\) 로 web page 의 hyperlink 가 있습니다. 각 page \(v\) 는 자신의 점수를 자신이 가진 links 의 개수만큼으로 나눠서 각각의 \(u\) 에게 전달합니다. \(u\) 는 \(v\) 로부터 받은 점수의 합에 상수 \(c\) 를 곱합니다. 그리로 전체 마디의 개수 \(N\) 의 역수인 \(\frac{1}{N}\) 의 \((1 - c)\) 배 만큼을 더합니다. \(c\) 는 \([0, 1]\) 사이의 상수입니다. 논문에서는 0.85 를 이용하였습니다.
\[PR(u) = c \times \sum_{v \in B_u} \frac{PR(v)}{N_v} + (1 - c) \times \frac{1}{N}\]Steady state and Dangling nodes
Citations 만을 생각하면 아래의 식만으로도 충분합니다. 그러나 그래프가 cyclic 이지 않으면 제대로된 계산을 할 수 없습니다. Cyclic network (graph) 란 한 마디에서 출발하여 다른 마디를 거쳐 다시 출발한 마디로 돌아올 수 있는 길이 있는 네트워크입니다. Web page hyperlinks 에서는 한 page 에서 출발하여 hyperlinks 를 누르다보면 자신의 page 로 돌아올 수 있다는 의미입니다.
\[PR(u) = \sum_{v \in B_u} \frac{PR(v)}{N_v}\]PageRank 는 개미의 이동 모델로 설명하기도 합니다. N 개의 마디가 존재하는 graph 에 각 마디마다 공평하게 \(\frac{1}{N}\) 마리의 개미를 올려둡니다. 한 스텝마다 모든 마디의 개미들은 links 를 따라 연결된 다른 마디로 이동합니다. 한 마디의 links 가 두 개 이상이라면 개미들은 공평히 나눠져서 링크를 따라 이동합니다. 이 부분이 위 식의 \(\frac{PR(v)}{N_v}\) 입니다. Backlinks 가 많은 마디에는 많은 개미가 모입니다. 이 과정을 한 번이 아닌 여러 번 수행합니다.
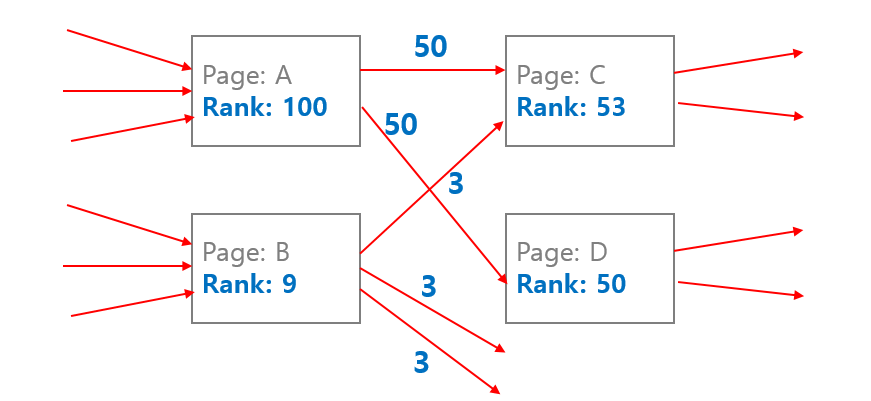
이러한 과정을 확률 분야에서는 Markov model 이라 합니다. 확률 모형을 이용하여 매 스텝마다 변하는 시스템을 표현합니다. 개미가 이동하는 비율은 Markov model 의 transition matrix 에 해당합니다. 그리고 Markov model 에서는 이런 과정을 여러 번 반복하면 각 마디에 존재하는 개미의 숫자가 변하지 않는 시점 (steady state) 이 생깁니다. 대략 반복횟수 50 번 정도면 충분합니다.
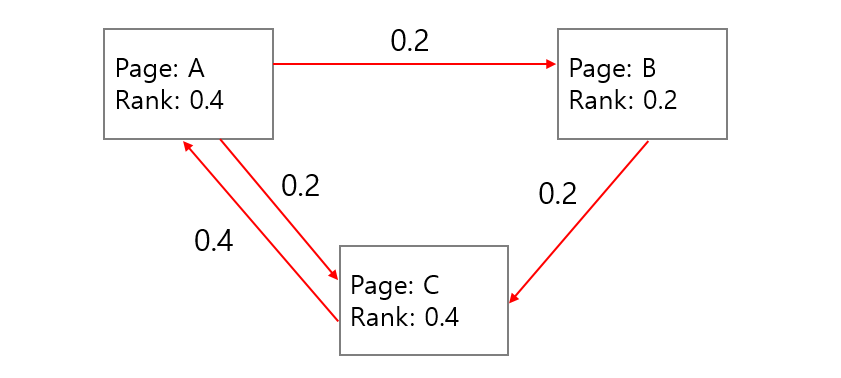
그러나 어떤 마디는 backlinks 만 있고 다른 마디로 연결되는 links 가 없을 수도 있습니다 (dangling node). 이 경우에 개미는 들어오기만 할 뿐 다른 마디로 나가질 못합니다. 이 문제를 해결하기 위해 각 마디에 존재하는 개미의 \(c=0.85\), 85% 만큼만 남겨두고 \((1 - c)\), 15% 는 임의의 노드로 보냅니다. 모든 마디에서 15% 의 개미가 다른 마디로 나뉘어서 보내지기 때문에 각 마디는 \(\frac{1 - c}{N}\) 의 개미가 새로 유입되는 효과가 있습니다. \(\frac{1 - c}{N}\) 은 dangling nodes 에 의하여 cyclic graph 가 만들어지지 않는 문제를 해결하기 위한 방법입니다. Random jump 를 통하여 모든 마디는 연결이 되며, cyclic network 가 됩니다.
\(\frac{1 - c}{N}\) 는 PageRank 의 bias 역할을 합니다. 이부분을 유용하게 활용하면 personalized PageRank 가 됩니다.
HITS
Concept
PageRank 와 비슷한 시기에, 비슷한 아이디어로, 비슷한 문제를 해결한 다른 알고리즘도 있습니다. HITS 는 Jon Kleinberg 의 알고리즘입니다. 네트워크, 확률, 클러스터링, 최적화, dynamic system, … 등 정말 많은 영역에서 연구를 하시는 분입니다 (이 분도 팬질하는 교수님입니다). HITS 는 Hyperlink-Induced Topic Search 의 약자입니다.
HITS 의 아이디어는 아래와 같습니다. 정말 좋아하는 구절이라서 원문을 그대로 인용하였습니다. 중요한 웹페이지는 좋은 웹페이지로부터 링크를 많이 받은 페이지이고, 각 페이지의 authority 는 중요한 웹페이지로부터의 링크가 많을수록 높다는 의미입니다.
I quotated following text from the paper, that is one of my favorate phrase.
Algorithm
위 문구는 그대로 공식으로 옮겨집니다. 마디 p 의 hub score 는 backlinks 의 출발 마디인 q 의 authority score 의 합입니다. 마디 p 의 authotiry score 는 backlinks 의 출발 마디인 q 의 hub score 의 합입니다. 이 식을 hub and authority score 가 수렴할 때 까지 반복합니다. 초기화는 모든 마디에 같은 값을 hub and authority score 로 설정하는 것입니다.
\[hub(p) = \sum_{q:(q \rightarrow p)} authority(q)\] \[authority(p) = \sum_{q:(q \rightarrow p)} hub(q)\]그러나 위 식 만으로는 각 score 가 수렴하지 않습니다. 점수의 합이기 때문에 반복할수록 그래프 내의 점수의 총 합이 커집니다. 그 총합을 맞춰주기 위하여 매 반복마다 hub and authority score 의 총합을 유지합니다. 그 값을 벡터라 생각하여 L2 normalization 을 합니다.
Pseudo code 는 아래와 같습니다.
- Step 1. Initialize hub(p) and authority(p) for all nodes
- Step 2. Update hub score \(hub(p) = \sum_{q:(q \rightarrow p)} authority(q)\)
- Step 3. Normalize hub score
- Step 4. Update authority score \(authority(p) = \sum_{q:(q \rightarrow p)} hub(q)\)
- Step 5. Normalize authority score
- Step 6. Repeat step 2 - 5 until it converges.
HITS vs PageRank
Authority score 와 hub score 를 같은 것으로 생각하면 아래처럼 식을 변형할 수도 있습니다. PageRank 와 다른 점은 개미가 연결된 다른 마디로 이동할 때 나뉘어지지 않고, 링크 개수만큼 복제되어 이동하는 것입니다. 개미의 전체 개수가 늘어난 것을 제어하기 위하여 normalize 를 수행하여 그래프 전체의 개미 숫자를 통제합니다.
\[score(p) = \sum_{q:(q \rightarrow p)} score(q)\]Eigen-vector problem?
PageRank 를 설명할 때 eigen vector problem 이라는 말이 자주 등장합니다. 앞서 PageRank 처럼 매 스텝마다 마디의 랭킹이 변하는 과정을 확률 모형으로 표현할 수 있는 문제를 Markov model 이라 하였습니다. 그리고 PageRank 의 랭킹값이 일정해지는 상태를 steady state 라 하였습니다. Markov model 에서 steady state 를 하나의 수식으로 계산하는 방법이 있습니다. 행렬의 eigen vector 를 찾는 문제와 같습니다. 하나의 수식으로 eiven vector 를 계산하는 방법을 선형대수적 해법 (algebraic solution) 이라 합니다.
하지만 수식을 모른다 하여도 앞선 개미의 이동 모형을 그대로 코드로 옮겨서 구현하면 steady state 의 값을 계산할 수 있습니다. 아래의 코드는 선형대수적 해법이 아닌, 직관을 그대로 코드로 옮긴 방법입니다.
Implementing PageRank with Python
Python 을 이용하여 선형대수적이지 않는 방법으로 PageRank 를 구현할 때에도 두 가지 방법이 있습니다. 개미가 각 마디를 이동하는 비율을 행렬로 표현할 수 있습니다. 첫번째 방법은 numpy 와 scipy.sparse 를 이용하면 구현하는 것으로, c 를 이용하기 때문에 빠른 계산이 가능합니다. 하지만 모든 마디가 미리 숫자로 표현되어 있어야 합니다. 속도 비교도 해볼겸, 이 부분은 나중에 따로 포스팅하겠습니다.
이번 포스트에서는 두번째 방법인 Python 의 dict 만을 이용하여 PageRank 를 구현합니다.
입력되는 데이터 G 의 형태는 dict dict 입니다. 대신 inbound graph 여야 합니다. G 의 첫번째 key 는 우리가 이번에 계산할 마디 v 입니다. 두번째 key 는 v 로 이동할 마디 u 입니다. 그리고 두번째 dict 의 value 는 u 에서 v 로 이동하는 비율입니다.
G[v][u] : proportion (u --> v)
그렇기 때문에 u 의 기준에서의 weight 의 총합은 1이어야 합니다. 이를 확인하는 normalize 함수를 만듭니다. G 는 반드시 inbound graph 여야 합니다.
def _normalize(G):
"""It returns outbound normalized graph
Arguments
---------
G: inbound graph dict of dict
"""
# Sum of outbound weight
# t: to node, f: from node, w: weight
W_sum = {}
for t, f_dict in G.items():
for f, w in f_dict.items():
W_sum[f] = W_sum.get(f, 0) + w
A = {t:{f:w/W_sum[f] for f,w in f_dict.items()} for t, f_dict in G.items()}
nodes = set(G.keys())
nodes.update(W_sum)
return A, nodesnormalize() 를 거친 그래프 A 와 마디집합 nodes 를 만듭니다. 각 마디의 초기 rank 는 마디의 개수의 역수인 1/N 입니다.
A, nodes = _normalize(G)
N = len(nodes) # number of nodes
ir = 1/N
rank = {n:ir for n in nodes}주어진 최대 반복 횟수 max_iter 동안 ranking 을 update 합니다. 모든 마디에 대하여 normalize 를 한 A 에서 from nodes 를 가져옵니다. 그 뒤 from node f 의 현재 ranking 인 rank[f] 에 from -> to 의 weight 인 w 를 곱하여 합을 구합니다. 이 rank_t 가 다음 스텝의 to ndoe 의 PageRank 입니다.
for _iter in range(1, max_iter + 1):
rank_new = {}
# t: to node, f: from node, w: weight
for t in nodes:
f_dict = A.get(t, {})
rank_t = sum((w*rank[f] for f, w in f_dict.items())) if f_dict else 0
rank_t = sr * rank_t + df * bias.get(f, ir)
rank_new[t] = rank_t반복을 반드시 max_iter 번 할 필요는 없습니다. 이를 위해서 모든 마디의 rank 와 rank_new 의 차이의 절대값을 diff 로 합칩니다. 그 값이 사용자가 지정한 converge_error 보다 작으면 max_iter 를 다 반복하지 않고 학습을 종료합니다.
diff = sum((abs(rank[n] - rank_new[n]) for n in nodes))
if diff < converge_error:
if verbose:
print('Early stopped at iter = {}'.format(_iter))
break사용자에 의하여 입력되는 damping factor 를 survival rate (sr), \(c\) initial rate (ir), \((1 - c)\) 로 바꾸는 부분과 initialize 하는 과정을 추가하여 PageRank 를 계산하는 pagerank 함수를 만듭니다.
def pagerank(G, bias=None, df=0.15,
max_iter=50, converge_error=0.001,verbose=0):
"""
Arguments
---------
G: Inbound graph, dict of dict
G[to_node][from_node] = weight (float)
df: damping factor, float. default 0.15
"""
if not bias:
bias = {}
A, nodes = _normalize(G)
N = len(nodes) # number of nodes
sr = 1 - df # survival rate (1 - damping factor)
ir = 1 / N # initial rank
# Initialization
rank = {n:ir for n in nodes}
# Iteration
for _iter in range(1, max_iter + 1):
rank_new = {}
# t: to node, f: from node, w: weight
for t in nodes:
f_dict = A.get(t, {})
rank_t = sum((w*rank[f] for f, w in f_dict.items())) if f_dict else 0
rank_t = sr * rank_t + df * bias.get(t, ir)
rank_new[t] = rank_t
# convergence check
diff = sum((abs(rank[n] - rank_new[n]) for n in nodes))
if diff < converge_error:
if verbose:
print('Early stopped at iter = {}'.format(_iter))
break
if verbose:
print('Iteration = {}'.format(_iter))
rank = rank_new
return rankImplemented code in Github repository
위 코드는 github 의 lovit/pagerank 에 올려두었습니다.
from pagerank import pagerank
pr = pagerank(G_inbound, # inbound graph. doesn't care key type.
bias=None, # bias for personalized pagerank
df=0.15, # damping factor
max_iter=50,
converge_error=0.001,
verbose=0
)References
- Kleinberg, J. M. (1999). Authoritative sources in a hyperlinked environment. Journal of the ACM (JACM), 46(5), 604-632.
- Page, L., Brin, S., Motwani, R., & Winograd, T. (1999). The PageRank citation ranking: Bringing order to the web. Stanford InfoLab.