k-means clustering 은 각 군집의 모양이 구 형태로 convex 할 때 작동하며, 데이터 분포가 복잡할 경우에는 잘 작동하지 않는다 알려져 있습니다. 복잡한 형태의 분포를 띄는 데이터의 군집화를 위해서 clustering ensemble 방법들이 이용될 수 있습니다. Ensemble 의 기본 군집화 알고리즘으로 k-means 를 이용할 수도 있습니다. 이번 포스트에서는 데이터 분포가 복잡한 경우에 적용할 수 있는 군집화 방법인 k-means ensemble 을 다룹니다. 이를 위해 sparse matrix 형태의 affinity matrix 를 이용하는 agglomerative clustering 알고리즘도 구현합니다.
k-means Introduction
k-means 는 다른 군집화 알고리즘과 비교하여 매우 적은 계산 비용을 요구하면서도 안정적인 성능을 보입니다. 그렇기 때문에 큰 규모의 데이터 군집화에 적합합니다. 문서 군집화의 경우에는 문서의 개수가 수만건에서 수천만건 정도 되는 경우가 많기 때문에 다른 알고리즘보다도 k-means 가 더 많이 선호됩니다. k-partition problem 은 데이터를 k 개의 겹치지 않은 부분데이터 (partition)로 분할하는 문제 입니다. 이 때 나뉘어지는 k 개의 partiton 에 대하여, “같은 partition 에 속한 데이터 간에는 서로 비슷하며, 서로 다른 partition 에 속한 데이터 간에는 이질적”이도록 만드는 것이 군집화라 생각할 수 있습니다. k-means problem 은 각 군집 (partition)의 평균 벡터와 각 군집에 속한 데이터 간의 거리 제곱의 합 (분산, variance)이 최소가 되는 partition 을 찾는 문제입니다.
\[\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}\]우리가 흔히 말하는 k-means 알고리즘은 Lloyd 에 의하여 제안되었습니다. 이는 다음의 순서로 이뤄져 있습니다.
- k 개의 군집 대표 벡터 (centroids) 를 데이터의 임의의 k 개의 점으로 선택합니다.
- 모든 점에 대하여 가장 가까운 centroid 를 찾아 cluster label 을 부여하고,
- 같은 cluster label 을 지닌 데이터들의 평균 벡터를 구하여 centroid 를 업데이트 합니다.
- Step 2 - 3 의 과정을 label 의 변화가 없을때까지 반복합니다.
Lloyd k-means 는 대체로 빠르고 안정적인 학습 결과를 보여줍니다만, 몇 가지 단점을 가지고 있습니다. 그 중 하나는 k-means 는 군집의 모양이 구 형태처럼 convex 하다고 가정합니다. 하지만 아래와 같은 데이터는 군집의 형태가 convex 가 아니기 때문에 k-means 가 제대로 작동하지 않습니다.
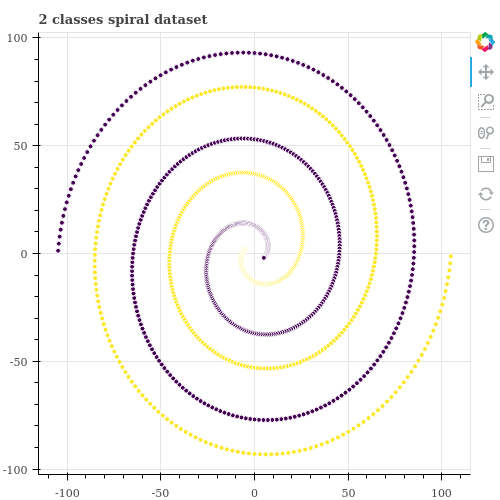
아래는 원점 근방에서 시작하며 서로 위상이 180 도 만큼 다른 두 개의 나선으로 이뤄진 데이터입니다. 우리는 아래의 그림에서 두 데이터가 보라색과 검정색으로 나뉘어지길 원하지만 k-means 는 나선형 데이터처럼 분포가 복잡한 (군집의 모양이 convex 가 아닌) 경우에는 잘 작동하지 않습니다. 아래처럼 k-means 를 학습한 뒤 결과를 확인합니다. 이를 위하여 Scikit-learn 의 KMeans 를 이용합니다.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, n_init=1, max_iter=10)
label = kmeans.fit_predict(X)
scikit-learn 을 이용하여 데이터를 두 개의 군집으로 나누면 아래처럼 공간을 이분 (bipartite) 하는 군집화 결과가 학습됩니다. k-means 입장에서는 공간을 절반으로 나누는 것이 앞서 설명한 비용 함수 (각 군집의 중심과 군집에 속한 점들 간의 거리 제곱의 합)를 최소화 할 수 있기 때문입니다.
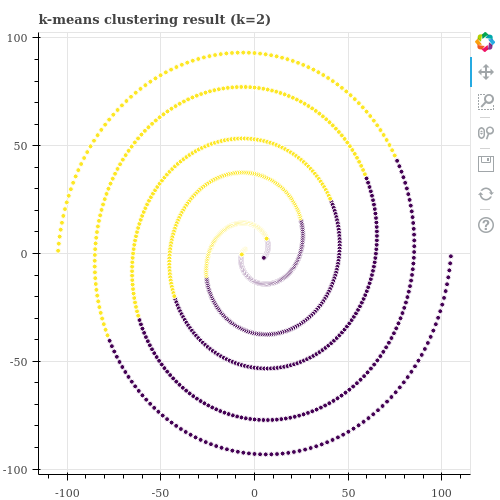
이번 포스트에서는 이 데이터를 2 개의 군집으로 학습하는 방법으로, k-means ensemble 을 알아봅니다. 그리고 k-means ensemble 을 할 때 주의해야 하는 점에 대해서도 알아봅니다. 이 포스트에서 이용한 데이터는 인공적으로 생성한 데이터입니다. 아래의 repository 에 데이터 생성 함수와 튜토리얼 코드를 올려두었습니다.
아래 코드는 위 repository 의 코드를 이용하여 데이터를 생성하고 scatter plot 을 그리는 과정입니다.
from bokeh.plotting import figure, output_notebook, output_file, reset_output, save, show
from bokeh.io import export_png
from data import generate_twin_spiral_data
from plot import draw_scatterplot
X, y = generate_twin_spiral_data()
p = draw_scatterplot(X, y, title='2 classes spiral dataset', width=500, height=500)
Kernel k-means and Spectral Clustering
이처럼 분포가 복잡한 데이터를 군집화 하기 위해 Spectral Clustering 과 같은 방법이 제안되기도 했지만, 이 역시 parameter setting 을 잘 설정해주지 않으면 군집화가 잘 되지 않습니다. 이는 Kernel k-means 역시 동일합니다. 어떠한 kernel function 을 이용할 것인지에 따라 데이터 간의 affinity 정의가 달라지기 때문에 군집화 결과가 다르게 학습될 수 있습니다.
실제로 Scikit-learn 의 SpectralClustering 을 이용하여 위 데이터를 2 개의 군집으로 학습해 봅니다. 사용자가 설정할 수 있는 parameters 가 있는데, 어떻게 설정하여도 제대로 나뉘어지지 않았습니다. 우리가 눈으로 볼 수 있는 2 차원 공간의 데이터인데도 적절한 parameters 를 찾을 수 없다면, 우리가 눈으로 확인하기 어려운 고차원 공간의 대량의 데이터라면 군집화가 잘 되지 않는 알고리즘이라 생각해야 합니다 (좋은 학습 결과를 얻기가 까다로운 알고리즘입니다).
from sklearn.cluster import SpectralClustering
spectral_clustering = SpectralClustering(n_clusters=2)
labels = spectral_clustering.fit_predict(X)
p = draw_scatterplot(X, label, title='Spectral clustering result (k=2)', width=500, height=500)
export_png(p, 'kmeans_ensemble_scresult.png')
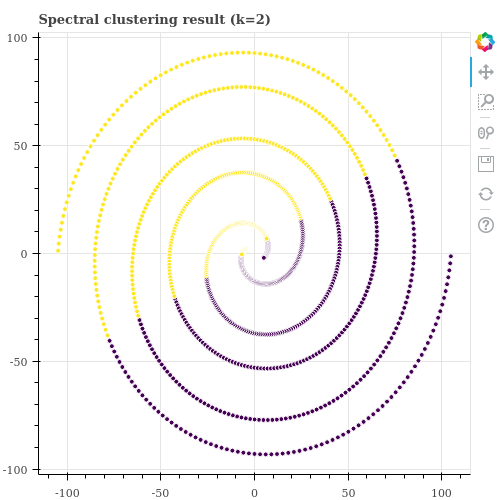
Clustering (k-means) ensemble
이러한 문제의 해법으로 제안된 것 중 하나는 clustering ensemble 입니다. 군집화 알고리즘은 어떤 것을 이용하여도 관계 없습니다. k-means 가 학습 속도가 빠르기 때문에 이를 이용하여 앙상블을 할 수 있습니다.
k-means ensemble 은 간단합니다. 우리가 알고 있는 k-means 알고리즘을 여러 번 반복하여 학습합니다. 한 번의 k-means 의 학습 결과 각 점들의 군집 아이디 (labels) 를 얻을 수 있습니다. 이 정보로부터 같은 군집에 속한 점들 간에 co-occurrence 를 1 씩 더합니다. 예를 들어 point 1, point 2 가 같은 군집에 속하였다면 아래처럼 co-occurrence 를 더합니다. 다음 번 k-means 의 학습 결과에서도 point 1, point 2 가 같은 군집에 속하였다면 (그 군집의 label 이 무엇인지는 관계없이) co-occurrence 값을 1 추가합니다.
from collections import defaultdict
cooccurrence = defaultdict(int)
cooccurrence[(1, 2)] += 1
k-means 를 100 번 학습하면 어떤 두 점은 최대 100 번의 co-occurrence 를 얻을 수 있고, 어떤 점은 한 번도 같은 군집에 속한 적이 없을 수도 있습니다. 이 co-occurrence 값을 점간의 affinity 로 이용합니다. 아래의 코드에서 X 는 scipy.sparse.matrix 나 numpy.ndarray 와 같은 행렬로 표현된 데이터 입니다. n_ensembles 는 k-means 의 반복 횟수입니다. n_ensemble_units 은 기본 k-means 를 학습할 때의 clusters 의 개수입니다.
Scikit-learn 의 k-means 는 n_init 번의 k-means 를 실행하고 silhouette score 기준으로 가장 좋은 결과를 return 합니다. 그리고 매 실행마다 max_iter (기본값 300) 의 반복 계산을 합니다. k-means 는 이렇게 계산할 필요가 전혀 없습니다. 수렴이 빠르고 군집의 개수가 많으면 대체로 안정적인 학습 결과를 보이기 때문에 n_init = 1, max_iter = 20 으로 설정합니다. Co-occurrence 가 계산되면 이를 sparse matrix 로 만듭니다.
from collections import defaultdict
from sklearn.cluster import KMeans
n_rows = X.shape[0]
n_ensembles = 1000
n_ensemble_units = 100
cooccurrence = defaultdict(int)
for i_iter in range(n_ensembles):
base_kmeans = KMeans(
n_clusters = n_ensemble_units,
n_init = 1,
max_iter = 20
)
y = base_kmeans.fit_predict(X)
for label in np.unique(y):
indices = np.where(y == label)[0]
for i in indices:
for j in indices:
if i == j:
continue
key = (i, j)
cooccurrence[key] += 1
affinity = cooccurrence_as_csr_matrix(cooccurrence, n_rows)
파이썬의 dict 형식인 cooccurrence 의 key 는 두 점이며, value 는 co-occurrence 입니다. 두 점을 각각 rows, columns 로 만들어 csr sparse matrix 를 만듭니다. Sparse matrix 의 종류에 대한 설명은 이 포스트를 참고하세요.
Sparse matrix 를 만들 때 마지막 index 의 점들 간에 co-occurrence 가 없을 수도 있습니다. shape 을 (n_rows, n_rows) 처럼 설정하지 않으면 rows, cols 의 최대값을 shape 으로 이용합니다. 모든 점이 포함되지 않은 affinity matrix 가 만들어질 수도 있으니 반드시 shape 을 아래처럼 강제로 설정합니다.
from scipy.sparse import csr_matrix
def cooccurrence_as_csr_matrix(cooccurrence, n_rows):
n = len(cooccurrence)
rows = np.zeros(n)
cols = np.zeros(n)
data = np.zeros(n)
for ptr, ((i, j), c) in enumerate(cooccurrence.items()):
rows[ptr] = i
cols[ptr] = j
data[ptr] = c
csr = csr_matrix((data, (rows, cols)), shape=(n_rows, n_rows))
return csr
이 과정을 정리하여 아래와 같은 함수를 만듭니다. 데이터 X 를 입력받아 n_ensembles 번의 k-means 를 반복하여 scipy.sparse.matrix 형태의 affinity matrix 를 return 하는 함수입니다.
def train_cooccurrence(X, n_ensembles, n_ensemble_units, n_clusters):
...
return affinity_matrix
Sparse affinity matrix 를 이용하는 agglomerative hierarchical clustering 구현
점들 간의 pairwise similarity (affinity) 를 알기 때문에 이를 이용하여 agglomerative hierarchical clustering 을 수행합니다. 군집의 개수가 k 가 될때까지 작은 군집들을 병합하면 됩니다. Ensemble 에 이용하는 기본 k-means 를 학습할 때, 군집의 개수를 충분히 크게 설정하면 affinity matrix 의 sparsity 가 높습니다. Affinity matrix 는 hierarchical clustering 이 이용하는 similarity matrix 입니다. 부르는 이름이 좀 다양합니다만, 모두 같은 의미입니다.
우리는 계산이 간단한 single linkage 를 이용하는 agglomerative hierarchical clustering 알고리즘을 구현합니다. Single linkage 는 거리가 가장 가까운 (유사도 가장 큰) 두 점을 이어 점들이 모두 이어질 때 까지 (모든 점이 하나의 군집에 속할 때 까지) 이를 반복합니다 (이는 Minimum Spanning Tree 와 같습니다).
most_similars 는 affinity matrix 의 정보를 COO matrix 처럼 (row, colume, value) 형태로 저장한 list of tuple 입니다. 그리고 이를 value (similarity) 기준 역순으로 정렬합니다. List 의 맨 앞의 값은 유사도가 가장 큰 두 점들입니다.
def single_linkage(affinity, n_clusters=2):
most_similars = []
n = affinity.shape[0]
rows, cols = affinity.nonzero()
data = affinity.data
for i, j, d in zip(rows, cols, data):
if i < j:
most_similars.append((i, j, d))
sorted_affinity = sorted(most_similars, key=lambda x:x[2], reverse=True)
idx_to_c 는 각 점이 어떤 군집에 속했는지에 대한 map 이며, c_to_idxs 는 각 군집에 속한 점들의 map 입니다. 초기화에서는 모든 점들이 각자의 군집을 만듭니다. 군집들이 병합되는 과정을 기록할 history 를 만들어둡니다. 그리고 다음 번 병합 (merging) 이 되는 군집의 idx 는 new_c 입니다. n 개의 점이 0 부터 n-1 까지의 cluster id 를 지녔으므로 n 으로 초기화 합니다.
def single_linkage(affinity, n_clusters=2):
...
idx_to_c = [i for i in range(n)]
c_to_idxs = {i:{i} for i in range(n)}
new_c = n
history = []
n_iters = 0
군집화 과정의 구현은 간단합니다. 우리는 모든 점이 하나의 군집으로 묶일 때까지 기다릴 필요는 없습니다. 군집의 개수가 우리가 입력한 n_clusters 보다 크고 정렬된 affinity 의 list 가 비어있지 않으면 군집의 병합 과정을 반복합니다.
List 의 맨 앞의 값을 pop 합니다. 이 두점은 아직 같은 군집에 있지 않은 점들입니다. 이들이 속한 군집의 아이디인 ci, cj 를 가져오고, 이 군집에 속한 점들을 union 으로 묶습니다. 그리고 union 에 속한 점들은 모두 new_c 의 cluster id 로 re-assign 합니다. 이전 군집 ci, cj 에 대한 정보를 지우면 군집의 merge 과정은 끝납니다.
def single_linkage(affinity, n_clusters=2):
...
while len(c_to_idxs) > n_clusters and sorted_affinity:
# Find a new link
i, j, sim = sorted_affinity.pop(0)
ci = idx_to_c[i]
cj = idx_to_c[j]
# merge two clusters
union = c_to_idxs[ci]
union.update(c_to_idxs[cj])
for u in union:
idx_to_c[u] = new_c
c_to_idxs[new_c] = union
del c_to_idxs[ci]
del c_to_idxs[cj]
군집이 합쳐지는 과정을 기록할 수도 있습니다. Merge 라는 namedtuple 을 만듭니다. child0, child1 이 ci, cj 입니다. 그리고 두 군집이 합쳐져 새로 부여받은 new_c 를 parent 에 저장합니다.
그 다음으로는 (row, column, value) 의 row 와 column 이 모두 union 에 속한 경우를 sorted_affinity 에서 제거합니다. 두 점이 하나의 군집으로 묶일 일은 이후로 없기 때문입니다 (이미 하나의 군집입니다).
마지막으로 다음 번 합쳐지는 군집에 부여할 cluster id (new_c) 를 1 증가시킵니다.
from collections import namedtuple
Merge = namedtuple('Merge', 'parent child0 child1 similarity')
def single_linkage(affinity, n_clusters=2):
...
while len(c_to_idxs) > n_clusters and sorted_affinity:
...
# log merging history
history.append(Merge(new_c, ci, cj, sim))
# Remove already merged links
sorted_affinity = [pair for pair in sorted_affinity
if not ((pair[0] in union) and (pair[1] in union))]
# Increase new cluster idx
new_c += 1
n_iters += 1
학습이 종료되면 idx_to_c 에는 각 점들이 속한 군집의 cluster id 가 저장되어 있습니다. 하지만 이 값은 0 부터 시작하는 값이 아닙니다. Merging 을 하면서 cluster id 를 계속 증가하였으니까요. numpy.unique 함수를 이용하여 unique cluster id 를 확인한 뒤, 이들을 0 부터 n_clusters - 1 로 re-numbering 합니다.
import numpy as np
def single_linkage(affinity, n_clusters=2):
...
labels = np.asarray(idx_to_c)
unique = np.unique(labels)
indices = [np.where(l == labels)[0] for l in unique]
for l, idxs in enumerate(indices):
labels[idxs] = l
return history, labels
이 부분을 합쳐 k-means ensemble 함수를 만들 수 있습니다. history 나 affinity 가 필요하다면 이를 따로 저장해둡니다.
def kmeans_ensemble(X, n_ensembles, n_ensemble_units, n_clusters):
affinity = train_cooccurrence(X, n_ensembles, n_ensemble_units, n_clusters)
history, labels = single_linkage(affinity, n_clusters)
return labels
k-means Ensemble 구현체
정리하면 k-means ensemble 은 여러 번의 k-means 학습 결과를 통하여 점들 간의 co-occurrence 를 학습하고, 이를 affinity matrix 로 이용하여 agglomerative clustering 을 수행합니다. 이 간단한 방법이 꾀 잘 작동합니다. 또한 parameter setting 에 대한 기준도 어느 정도 명확합니다. 단, 계산 비용이 싸지는 않습니다. 대체로 ensemble 을 위해 학습하는 k-means 의 반복 횟수가 많기 때문입니다.
여하튼 이 과정을 KMeansEnsemble 에 구현하였습니다. 구현체는 여기 github repository 에 올려두었습니다. Parameter 는 다음과 같습니다.
n_clusters : 최종적으로 학습하고 싶은 군집의 개수
n_ensembles : 기본 k-means 의 반복 학습 횟수
n_ensemble_units (n_units) : 기본 k-means 학습 시의 k 값
from kmeans_ensemble import KMeansEnsemble
n_clusters = 2
n_ensembles = 1000
n_units = 100
n_data = X.shape[0]
kmeans_ensemble = KMeansEnsemble(n_clusters, n_ensembles, n_units)
labels = kmeans_ensemble.fit_predict(X)
Sparsity 도 계산할 수 있습니다. 같은 점들 간에는 co-occurrence 를 계산하지 않았기 때문에 이 개수인 n_data 를 추가하였습니다. 그래도 97.1 % 의 pairs 은 co-occurrence 가 없습니다. 왠만한 점들은 서로 유사도가 없다고 해석할 수 있습니다.
nnz = kmeans_ensemble.affinity.nnz
sparsity = 1 - ((n_data + nnz) / (n_data ** 2)) # 0.9709
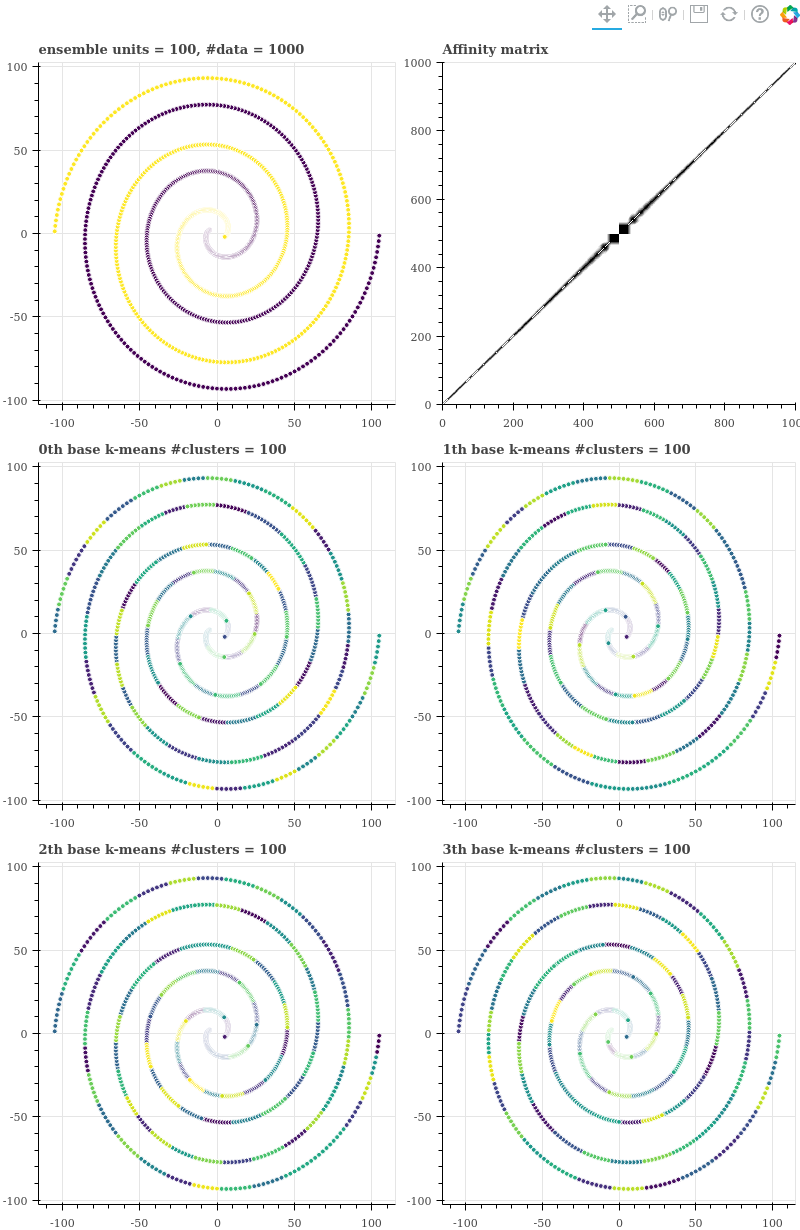
우리는 parameter 를 다양하게 하여 실험을 할 것이기 때문에 그림을 그리는 부분을 함수로 만듭니다. (3, 2) 크기의 grid plots 을 그립니다. 좌측 첫 줄을 (0, 0) 이라 할 때, (0, 0) 은 k-means ensemble 을 통하여 학습한 두 개의 군집화 결과 입니다. (0, 1) 은 k-means 의 반복 학습으로부터 얻은 co-occurrence matrix 입니다. 그 아래 (1, 0) ~ (2, 1) 까지의 네 개의 그림은 기본 k-means clustering 에서의 결과를 시각화 한 것입니다.
함수를 이용하여 grid plot 을 그리고 이를 png 파일과 html 로 저장합니다.
from bokeh.layouts import gridplot
def draw_debug_plots(X, kmeans_ensemble, labels, size=400):
n_data= X.shape[0]
title = 'ensemble units = {}, #data = {}'.format(n_units, X.shape[0])
p0 = draw_scatterplot(X, labels, title, width=size, height=size)
p1 = figure(title = 'Affinity matrix',
x_range=(0, n_data),
y_range=(0, n_data),
width=size, height=size
)
p1.image([n_ensembles - kmeans_ensemble.affinity.todense()], x=0, y=0, dw=n_data, dh=n_data)
gp = [p0, p1]
for i in range(4):
title = '{}th base k-means #clusters = {}'.format(i, n_units)
p = draw_scatterplot(X, kmeans_ensemble.base_history[i], title, width=size, height=size)
gp.append(p)
gp = gridplot([[gp[0], gp[1]], [gp[2], gp[3]], [gp[4], gp[5]]])
return gp
gp = draw_debug_plots(X, kmeans_ensemble, labels)
header = 'kmeans_ensemble_dataset_units{}'.format(n_units)
export_png(gp, header + '.png')
output_file(header + '.html')
save(gp)
reset_output()
기본 k-means 학습 시 데이터의 개수 1000 개에 군집의 개수 100 개를 이용하였기 때문에 (1, 0) 에서는 매우 작은 영역의 점들끼리만 같은 색으로 표현되어 있습니다. 데이터의 index 는 검은색 점들은 원점에 가장 가까운 점이 500 번이며, 원점에서 멀어질수록 1000 에 가까워집니다. 보라색 점들 중 가장 가까운 점의 index 가 499 이며, 원점에서 멀어질수록 0 에 가까워집니다. 즉 affinity matrix 에서 가운데가 원점이며, 모서리로 갈수록 원점에서 멀어지는 점들입니다.
Affinity matrix 를 살펴보면 색이 다른 두 점들 간에는 co-occurrence 가 전혀 없었으며, 매우 가까이 위치한 점들끼리만 co-occurrence 를 지닙니다. 그래서 대각선의 날카로운 선 모양의 그림이 그려집니다.
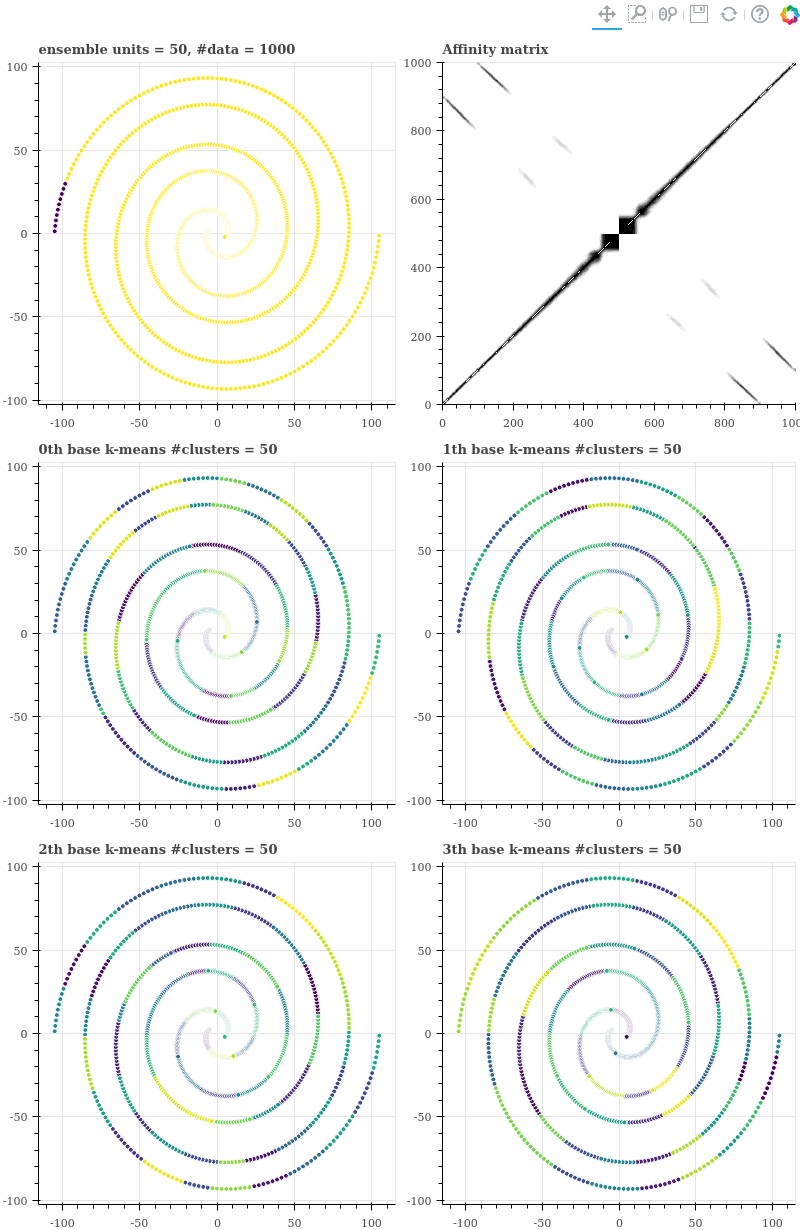
n_units = 50
kmeans_ensemble = KMeansEnsemble(
n_clusters=2, n_ensembles=1000,
n_ensemble_units=n_units)
labels = kmeans_ensemble.fit_predict(X)
gp = draw_debug_plots(X, kmeans_ensemble, labels)
Units 의 개수가 100 일 때에는 97.1 % 의 sparsity 를 보였지만, units 의 개수가 줄어드니 affinity matrix 의 sparsity 가 작아집니다. 유사한 점들이 늘어갑니다.
nnz = kmeans_ensemble.affinity.nnz
sparsity = 1 - ((n_data + nnz) / (n_data ** 2)) # 0.9255
그런데 기본 k-means 를 학습할 때의 k 를 조금만 줄여도 서로 다른 색의 점들 간에 co-occurrence 가 생깁니다. 그래서 affinity matrix 에 반대 방향의 대각선이 듬성듬성 생깁니다. 이는 (2, 1) 그림에서 x range = (10, 30), y range = (-90, -70) 부분에 서로 다른 선 위의 점들이 같은 색 (같은 군집)을 할당 받았음을 통해 확인할 수 있습니다.
k-means 가 군집의 형태를 원형으로 가정하기 때문에 벌어진 현상입니다. 그리고 그 결과 군집화 결과는 엉망이 됩니다. Agglomerative clustering 의 input 에 노이즈가 있기 때문입니다 (Agglomerative clustering 은 greedy 한 방식으로 군집을 병합하기 때문에 노이즈에 매우 민감합니다)
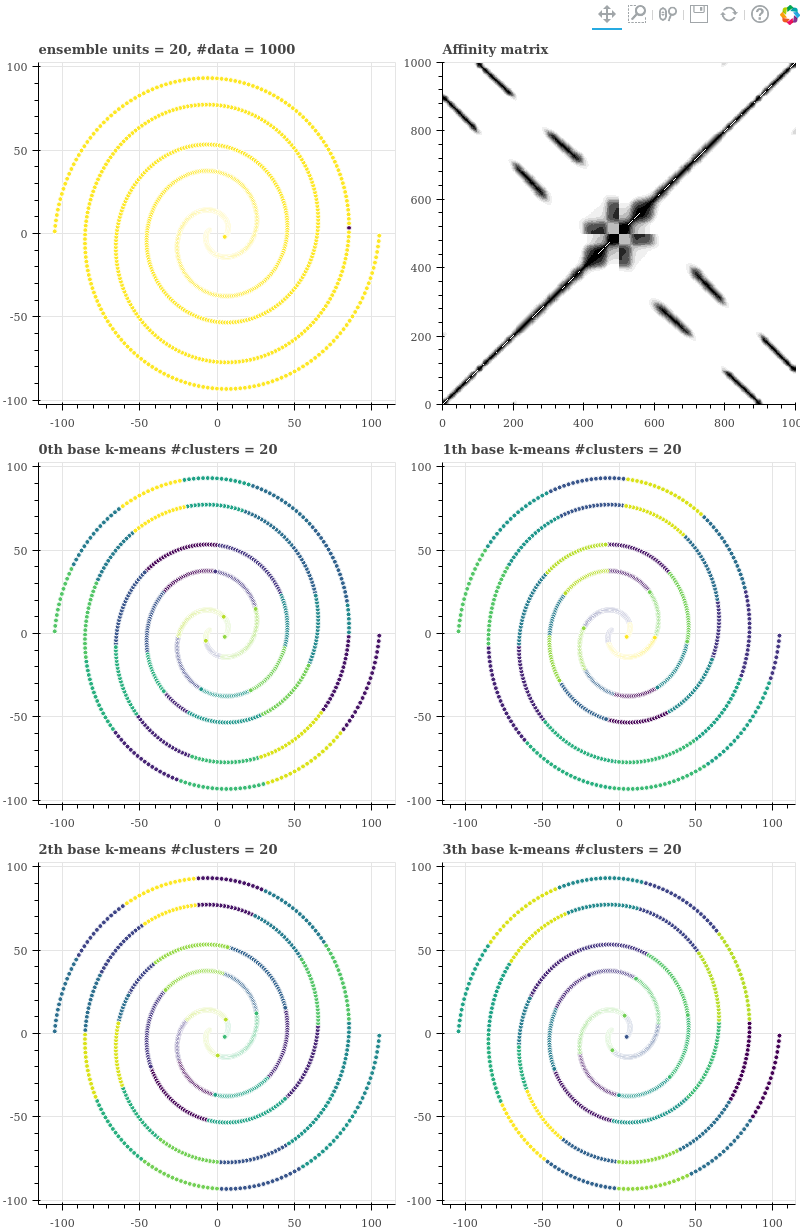
n_units = 20
kmeans_ensemble = KMeansEnsemble(
n_clusters=2, n_ensembles=1000,
n_ensemble_units=n_units)
labels = kmeans_ensemble.fit_predict(X)
gp = draw_debug_plots(X, kmeans_ensemble, labels)
Units 의 개수를 20 으로 줄이자 affinity matrix 의 sparsity 가 매우 많이 줄어듭니다.
nnz = kmeans_ensemble.affinity.nnz
sparsity = 1 - ((n_data + nnz) / (n_data ** 2)) # 0.7958
Units 의 개수를 좀 더 줄이면 affinity matrix 에 노이즈가 더 추가됩니다. 이미 ensemble 의 결과는 좋지 않기 때문에 굳이 비교하지는 않습니다. 아주 좁은 한 지역만 파란색 군집으로, 그 외의 거의 모든 점들이 노란색 군집으로 할당되었습니다.
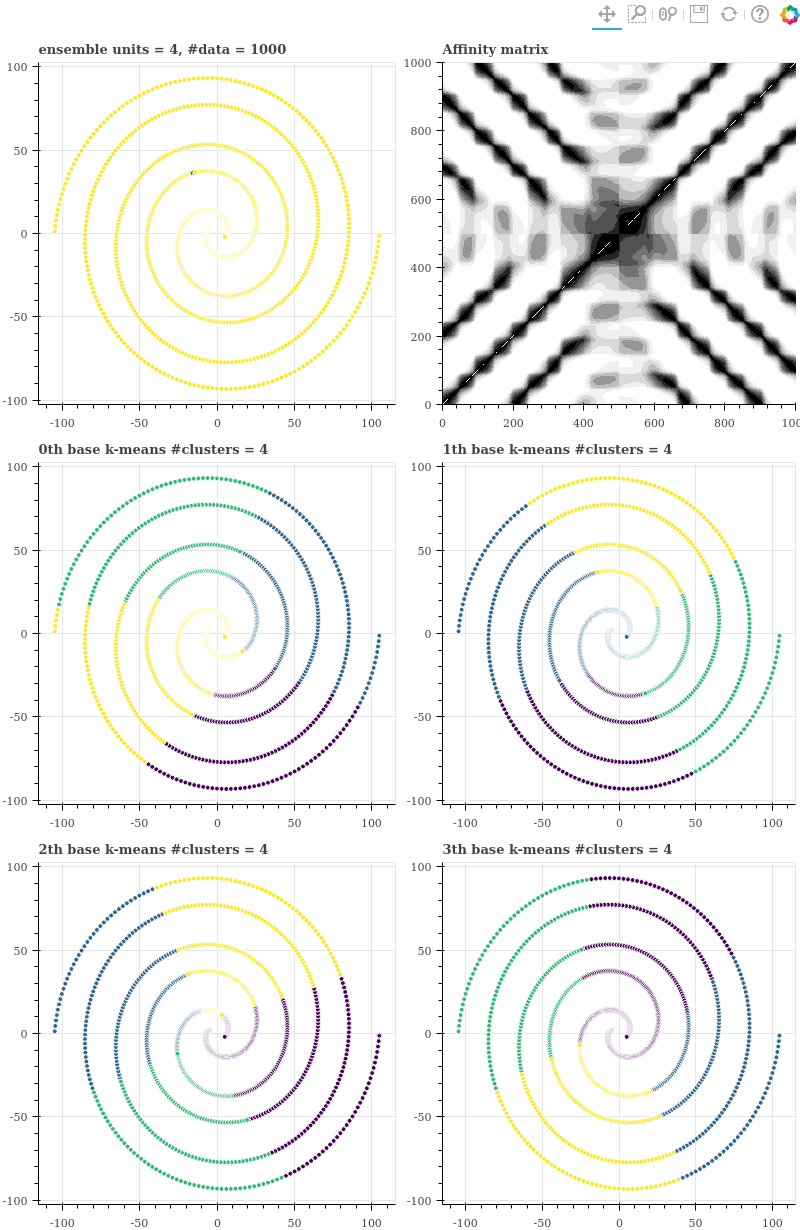
n_units = 4
kmeans_ensemble = KMeansEnsemble(
n_clusters=2, n_ensembles=1000,
n_ensemble_units=n_units)
labels = kmeans_ensemble.fit_predict(X)
gp = draw_debug_plots(X, kmeans_ensemble, labels)
이제는 co-occurrence 이 0 보다 큰 data point pairs 가 매우 많아졌습니다. 이는 units 을 작게 할 경우, 점들 간의 유사도를 잘 구분하지 못한다는 의미이기도 합니다.
nnz = kmeans_ensemble.affinity.nnz
sparsity = 1 - ((n_data + nnz) / (n_data ** 2)) # 0.2301
만약 units 의 개수를 4 처럼 매우 작게 설정한다면 affinity matrix 가 더 엉망이 됩니다.
k-means Ensemble as metric learning
Metric learning 은 k-nearest neighbor classifiers 와 같은 작업을 할 때 이용할 점들 간의 거리를 학습하는 machine learning 의 한 분야입니다. Word2Vec 과 같은 word representation learning 도 단어 간의 거리 정보를 학습하기 때문에 metric learning 으로 생각할 수도 있습니다. 차이점은 metric learning 은 두 점 간의 거리를 정의하는 함수를 학습하는 것이며, representation learning 은 두 점 간의 거리 함수가 아닌, 각 점들의 vector representation 을 학습하는 것입니다.
하지만 metric learning 은 주로 supervised learning 에서 이야기하는 방법입니다. 어떤 점이 가까워야 classification 이나 regression 이 더 잘 된다라는 점을 학습하려면 (X, y) 의 정보가 필요하기 때문입니다. 하지만 similarity matrix 자체가 두 점 간의 거리 함수이기 때문에 metric learning 으로 해석하여도 큰 무리는 없어 보입니다. 물론 unsupervised learning 이지만요.
두 점이 유사하다는 정보는 군집의 크기가 매우 작은 (군집의 개수가 많은) k-means 를 여러 번 학습하였더니 두 점이 자주 같은 군집으로 할당된다는 점에서 얻습니다. 두 점이 같은 군집에 자주 할당되려면 서로 근처에 있어야 합니다. 그리고 데이터의 형태가 고차원 공간이던지 sparse vector 이던지 혹은 metric 이 Manhattan, Euclidean, Cosine, Jaccard 이던지간에 가까운 점들 간의 거리는 0 에 가깝습니다. 군집의 크기를 매우 작게 설정했기 때문에 각 군집은 매우 작은 ball 을 이룹니다. 데이터 공간의 크기나 점들 간 distance metric 이 달라도 매우 가까이 있는 점들 (작은 ball 안에 함께 있는 점들)은 같은 군집에 속할 가능성이 높습니다. 즉 k-means ensemble 의 affinity matrix 는 nearest neighbor graph 의 similarity weight 입니다. 단 k-nearest neighbor graph 처럼 두 점이 가깝다, 아니다를 정확하게 나누지 않고 co-occurrence probability 로 표현한 것입니다.
이 거리는 데이터 분포에 큰 영향을 받지 않습니다. 복잡한 분포를 지니는 데이터라 하더라도 아주 작은 부분을 확대하면 단순하기 때문입니다. 마치 manifold 와 같습니다. 즉 k-means ensemble 은 metric learning 처럼 질좋은 pairwise similaries 를 학습하여 이를 최종 agglomerative clustering 에 이용하는 것입니다.
이는 kernel k-means 로 해석할 수도 있습니다. 반복 학습에 이용한 k-means 가 Euclidean distance 를 이용하였으므로, 이는 euclidean distance 에 기반하여 affinity 를 계산하는 RBF kernel k-means 의 근사 계산과 같습니다. 단 이를 위하여 (n, n) 크기의 kernel matrix 를 계산하지 않아도 되는 장점이 있습니다.
k-means Ensemble 에서의 주의점
앞의 내용을 살펴보면 ensemble 시 주의해야 할 점은 명확합니다. 기본 k-means 를 학습할 때 군집의 개수를 작게 설정하면 군집의 크기가 커지고, 다른 부분 공간 (manifold) 에 속한 점들 간에도 co-occurrence 가 있다고 착각하게 됩니다. 한 번의 k-means 학습 결과에서 우리가 얻는 정보는 고작 두 점이 같은 군집에 속했었는가 이기 때문입니다.
그렇기 때문에 k-means ensemble 에서는 기본 군집의 개수를 매우 크게 설정해야 합니다. 즉 k-means ensemble 을 수행할 때에는 데이터의 개수와 비교하여 한 군집에 아주 작은 개수의 점들만이 할당되도록 해야합니다.