Network based Nearest Neighbor Indexer

비싼 k-nearest neighbors 탐색 비용을 줄이기 위하여, 정확하지는 않더라도 빠르게 query point 와 비슷한 점들을 탐색할 필요가 있습니다. Approximated Nearest Neighbor Search (ANNS) 는 이를 위한 방법들입니다. Hash function 에 기반한 Locality Sensitive Hashing (LSH) 이 대표적이지만, network 를 이용하는 방법들도 많습니다. Small-world phenomenon 을 이용하는 방법으로 random neighbor graph 와 nearest neighbor graph 를 혼합하여 indexing 을 하는 방법이 있습니다. 이번 포스트에서는 network 의 특징을 이용하여 안정적인 성능으로 최인접 이웃을 검색하는 방법에 대하여 알아봅니다.

Nearest neighbor problem

최인접이웃 (nearest neighbors)은 regression, classification 에 이용되는 가장 기본적인 모델입니다. Non-parametric regression 은 주어진 query point 와 비슷한 점들의 y 값의 평균을 이용하여 regression 을 수행합니다.

$$y(q) = \sum_{x \in K_q} w(q, x) \times y(x)$$

where $w(q,x) = exp \left( -d(q, x) \right)$

Nearest neighbors 방법은 classification 에서는 Naive Bayes classifier 의 오차의 2 배 이하라고도 알려져 있으며, 가장 단순한 classifier 이기 때문에 다른 classifier 연구의 base model 로도 널리 사용됩니다. 일단 아주 직관적인 방법이기 때문에 이해도 쉽습니다.

그러나 하나의 query point 가 주어질 때 reference data 에서 가장 가까운 k 개의 점을 찾기 위해서는 모든 점들과의 거리를 계산해야 합니다. 만약 n 개의 점이 존재한다면 $O(n)$ 의 비용이 드는 매우 비싼 알고리즘이라 말합니다. 그러나 데이터의 크기가 커지면 절대 이런 brute-force 방법으로 계산을 하지 않습니다.

Approximated nearest neighbor search (ANNS) 란, 정확한 k 개의 최인접이웃을 찾지는 못하더라도, 비슷한 최인접이웃을 빠르게 찾기 위한 방법입니다. 이를 위한 방법은 다양합니다. i-Distance 같은 clustering 을 기반으로 하는 방법이나 tree 기반 방법들도 이용되었습니다. 이 다양한 방법들의 공통점은 벡터 공간을 단순한 공간으로 분할하여 이해한다는 것 (vector quantization) 입니다. 이 관점에서 더 발전된 모델은 hash function 을 이용하는 Locality Sensitive Hashing (LSH) 입니다. 정답이 있을만한 지역 코드 (hash code) 를 부여하여, 해당 지역만 빠르게 탐색하는 모델입니다. LSH 에 대한 자세한 설명은 이전의 포스트를 참고하세요

Locality Sensitve Hashing 계열 (이후에 LSH 의 단점들을 많이 보완한 후속연구들이 많이 제안되었습니다) index 들이 주로 연구가 되었지만, 그 방법만 있는 것은 아닙니다. Very sparse data 에 대해서는 여전히 inverted index 도 유용하며, netowrk 기반의 index 는 안정적인 검색 성능을 보여주기도 합니다.

이번 포스트에서는 network 기반으로 작동하는 nearest neighbor search algorithm 에 대하여 살펴봅니다.

Network based Nearest Neighbor Indexer

아래 그림은 원리 설명을 위한 예시 데이터입니다. 13 개의 2 차원의 데이터입니다.

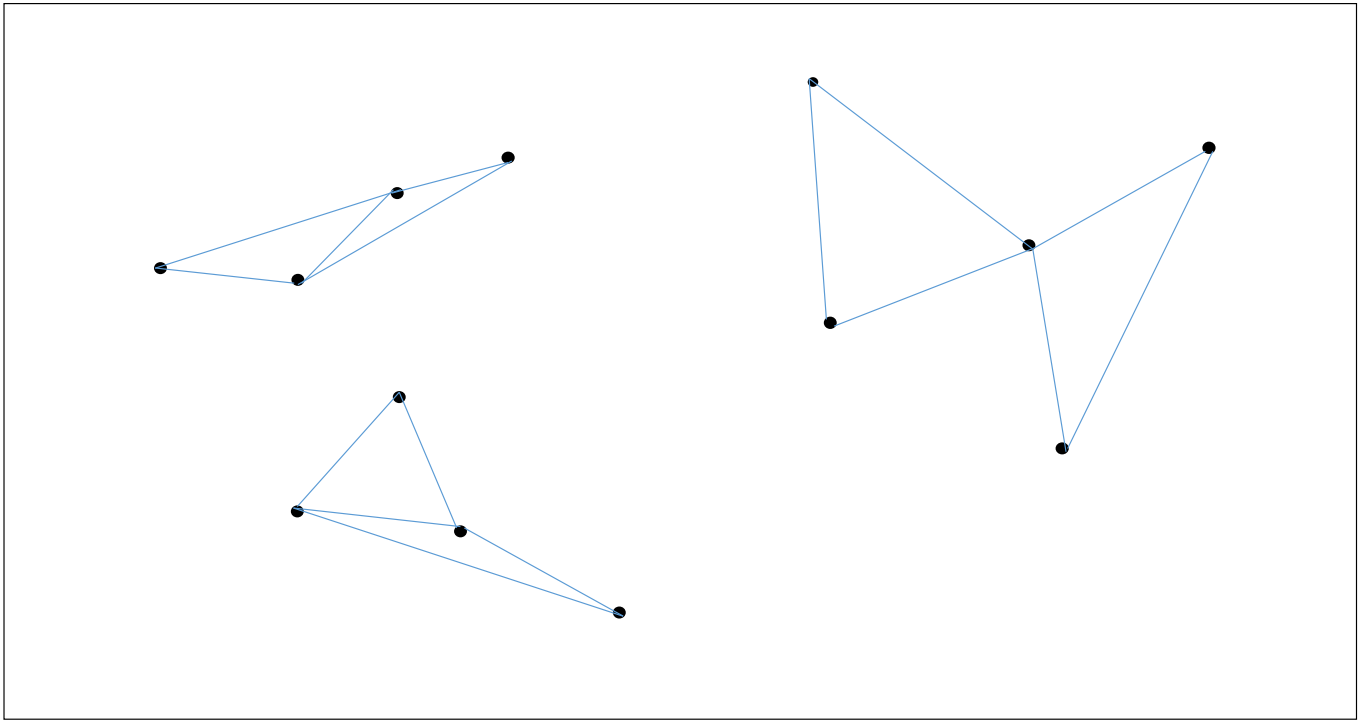
각 점마다 가장 가까운 2 개의 점들을 이어줍니다. 반드시 모든 점의 이웃의 갯수가 같을 필요는 없습니다. 작은 숫자이면 됩니다. 또한 단방향, 양방향이어도 상관없습니다. 자신과 가까운 점들을 알고 있는 것이 중요합니다.

여기서 한 가지, 우리가 풀려 하는 문제는 주어진 reference data 에 대하여 가장 가까운 점들을 빠르게 찾는 것이 아닙니다. 임의의 query point 에 대하여 빠르게 k-nearest neighbors 를 찾는 것입니다. Reference data 에 대한 k-nearest neighbor graph 를 만드는 것은 한 번의 training 입니다. Querying time 을 빠르게 만드는 것이 목표입니다.

물론 이 과정에서 NN-Descent 와 같은 neighbor graph 를 빠르게 만들어주는 알고리즘을 이용할 수도 있습니다.

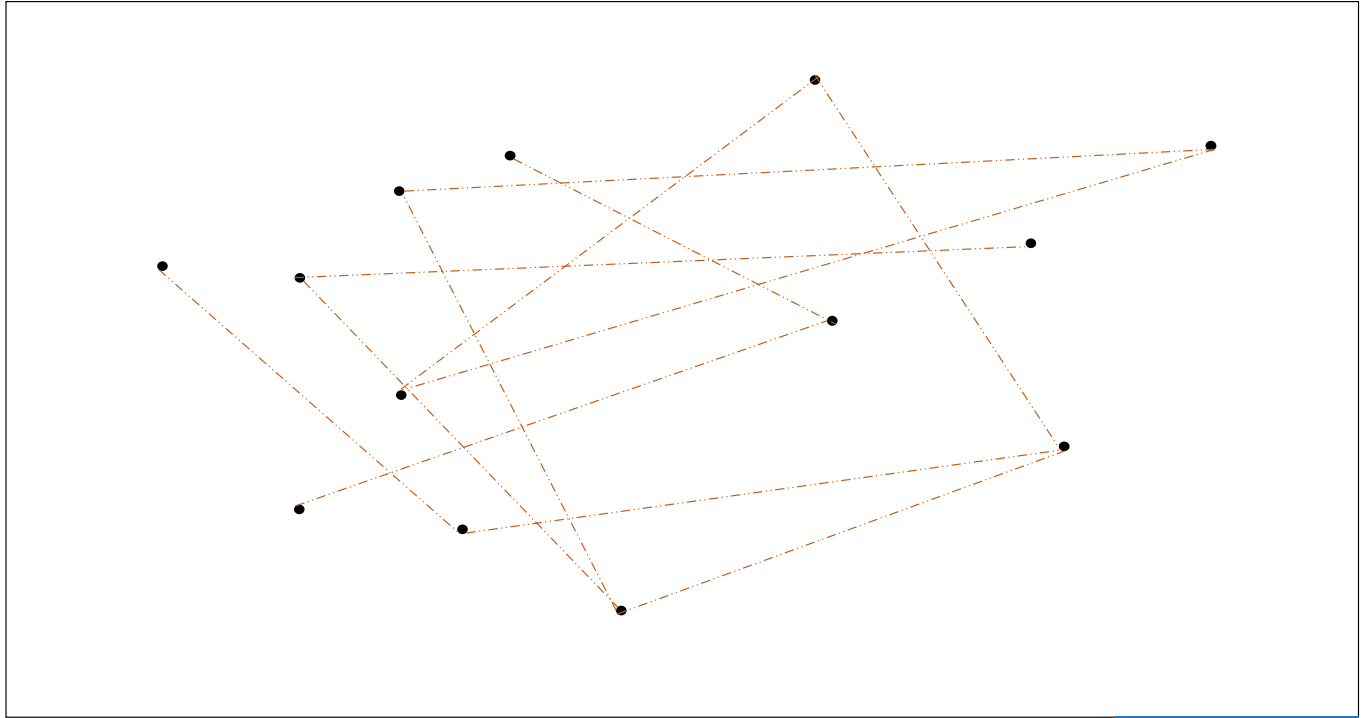
두번째로, 각 점 마다 임의로 몇 개의 점을 연결합니다. Random connected graph 입니다. 이는 한 지역에서 다른 지역으로 jump 를 할 수 있는, 일종의 고속도로 역할을 합니다.

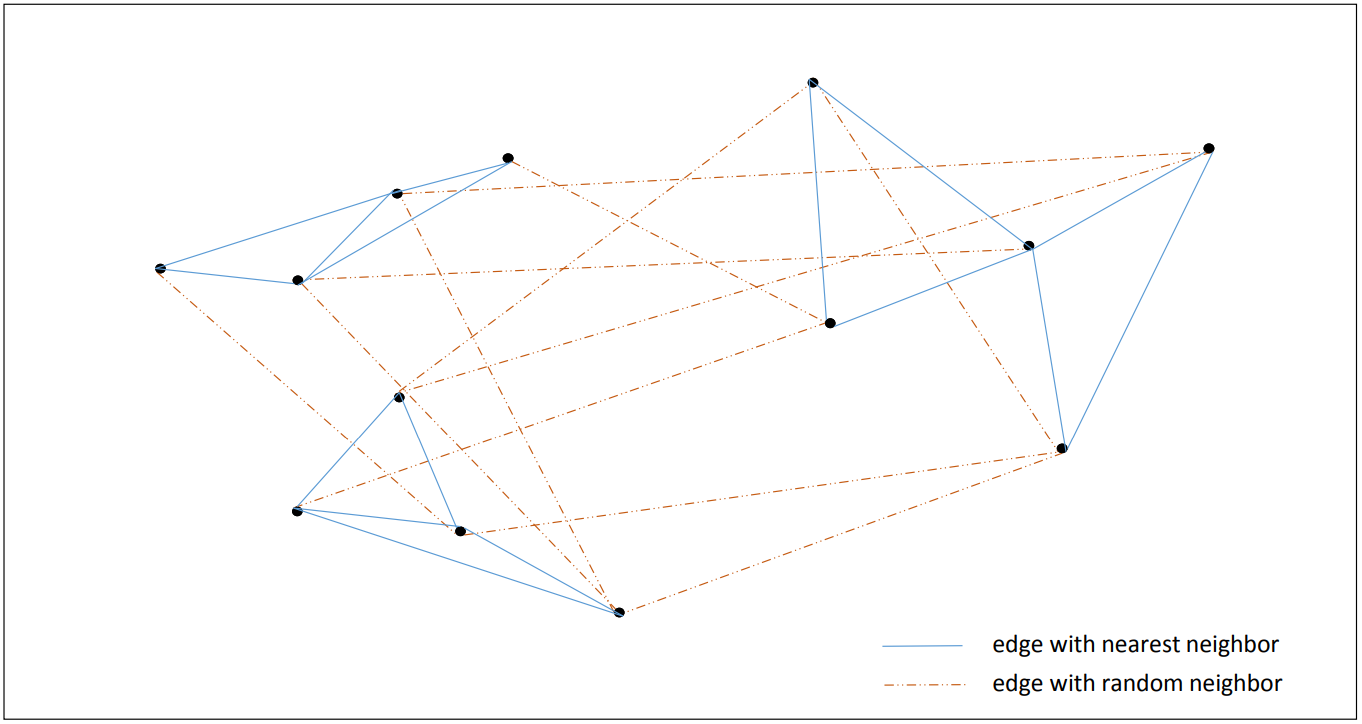
그리고 이 두 그래프 (nearest neighbor, random neighbor graph) 를 겹쳐줍니다. 이 과정까지가 indexing 입니다.

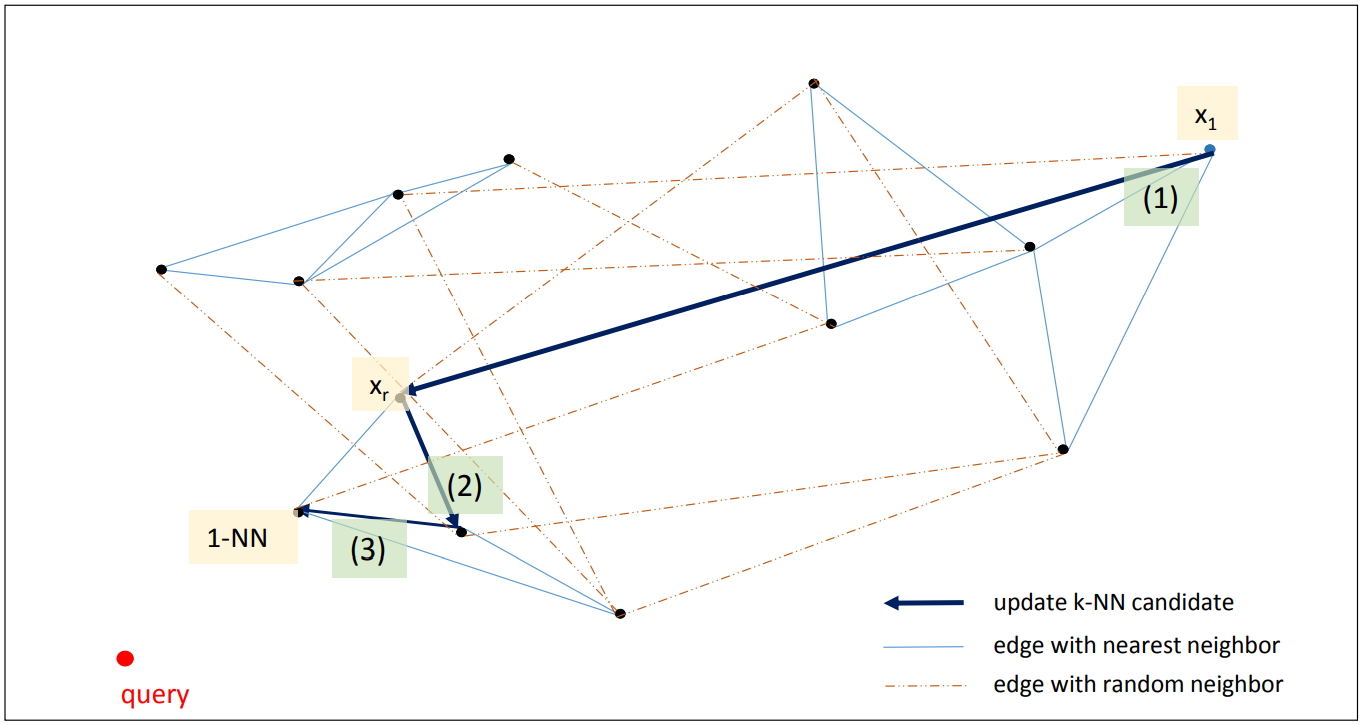
초기화: 하나의 query point 가 주어지면 p 개의 임의의 seed points 를 선택합니다. 아래 그림에서는 하나의 점 x1 을 선택하였습니다. x1 에서 이동할 수 있는 점 (nearest & random neighbor of x1) 중에서 query point 와 더 가까운 p 개의 점을 선택합니다 (아래 그림에서는 p=1 입니다).

반복 탐색: 임의로 선택하였기 때문에 query point 와 매우 먼 x1 이 선택되었고, nearest neighbor of x1 중에서는 query point 와 가까운 점이 없습니다. 대신 random neighbors 중에서 query point 와 가까운 xr 이 있습니다. 이 점을 frontier points 로 설정합니다. 현재까지 알려진 query point 와 가장 가까운 p 개의 점이라는 의미입니다. 이 점의 nearest & random neighbors 중에서 query point 와 가까운 점은 없는지 다시 탐색합니다. 점점 query point 와 가까운 점으로 frontier points 가 업데이트 됩니다.

반복 탐색 종료: 이 과정을 미리 설정된 max steps 번 만큼 반복하던지, frontier points 가 변하지 않을 때까지만 반복합니다.

p 는 k 이상이면 됩니다. 오히려 찾아야 하는 nearest neighbors 의 개수인 k 보다 더 큰 p 개의 frontier points 를 유지하는 것이 탐색을 더 빠르게 만들어줍니다.

Implementation

Index 는 index 함수와 search 함수가 필요합니다.

Skeleton

우리가 설정해야 하는 parameters 는 index 의 nearest, random neighbors 의 개수입니다. batch_size 는 brute force 방식으로 nearest neighbor 를 찾을 때 out-of-memory 를 방지하기 위한 변수입니다.

class NetworkBasedNeighbors:
    def __init__(self, X=None, n_nearest_neighbors=5,
        n_random_neighbors=5, batch_size=500,
        metric='euclidean', verbose=True):

        self.n_nearest_neighbors = n_nearest_neighbors
        self.n_random_neighbors = n_random_neighbors
        self.batch_size = batch_size
        self.verbose = verbose
        self.metric = metric
        self.buffer_factor = 3

        if X is not None:
            self.index(X)

    def index(self, X):
        ...

    def search_neighbors(self, query, k=5, max_steps=10, converge=0.000001):
        ...

index 함수

index() 함수를 구현합니다. Random neighbors 를 만드는 법은 간단합니다. numpy.random.randint 를 이용하면 0 부터 n_data 사이의 integer 를 (n_data, num_rn) 크기의 numpy.ndarray 로 만들어줍니다. 물론 이 때 한 점에 대한 random neighbors 에 같은 점이 포함될 수도 있습니다만, 이를 까다롭게 걸러낼 필요는 없습니다. Search 과정에서 중복된 점을 제거하면 됩니다. (그리고 중복된 점이 만들어질 가능성은 정말로 매우 작습니다)

most_closest_points 함수는 우리가 곧바로 구현할 함수입니다. X 의 각 점에 대하여, 자신을 제외한 topk 의 nearest neighbor point indices 를 return 하는 함수입니다.

import numpy as np

class NetworkBasedNeighbors:
    ...

    def index(self, X):
        n_data = X.shape[0]
        num_nn = self.n_nearest_neighbors
        num_rn = self.n_random_neighbors

        # set reference data
        self.X = X
        self.n_data = n_data

        if self.verbose:
            print('Indexing ...')

        # nearest neighbor indexing
        self.nn = most_closest_points(
            X, topk=num_nn, batch_size=self.batch_size,
            verbose=self.verbose)

        # random neighbor indexing
        self.rn = np.random.randint(n_data, size=(n_data, num_rn))

most_closest_points() 함수를 구현합니다. b 와 e 는 mini batch 의 시작과 끝점입니다. 이 구간의 X[b:e] 를 잘라 pairwise_distances(X[b:e], X) 를 계산합니다. b 부터 e 까지의 점 중에서 X 와 가장 가까운 점들을 찾습니다.

그런데 X 와 X 간의 거리를 계산하면 자신의 거리는 0 이기 때문에 가장 가까운 이웃에 자신이 포함됩니다. 이를 방지하기 위해서 dist_.copy().argsort(axis=1)[:,1:topk+1] 를 하였습니다. 1:topk+1 을 하면, 자신을 제외한 topk 개의 가장 가까운 점을 찾을 수 있습니다.

거리값 역시 dist_[:,1:topk+1] 를 통하여 자신을 제외한 거리를 고릅니다.

이들을 각각 idxs[b:e], dist[b:e] 에 저장합니다.

idxs, dist 는 X 의 모든 점에 대하여 자신과 가장 가까운 topk 개의 점들과 그들과의 거리값이 저장된 (n_data, topk) 크기의 numpy.ndarray 입니다.

import numpy as np
from sklearn.metrics import pairwise_distances

def most_closest_points(X, metric='euclidean',
    topk=5, batch_size=500, verbose=False):

    n_data = X.shape[0]
    num_batch = int(np.ceil(n_data/batch_size))

    idxs = np.zeros((n_data, topk), dtype=np.int)
    dist = np.zeros((n_data, topk))

    for batch_idx in range(num_batch):

        # batch index
        b = batch_idx * batch_size
        e = (batch_idx + 1) * batch_size

        # batch distance computation
        dist_ = pairwise_distances(X[b:e], X, metric=metric)

        # find closest points
        idxs_ = dist_.copy().argsort(axis=1)[:,1:topk+1]
        idxs[b:e] = idxs_

        # select distance of the closest points
        dist_.sort(axis=1)
        dist[b:e] = dist_[:,1:topk+1]

    return dist, idxs

search 함수

앞서 indexing 하는 함수를 만들었으니, 이번에는 k-nearest neighbors 를 찾는 search_neighbors() 함수를 구현해봅니다.

buffer_size 는 k 개의 nearest neighbors 를 찾는 동안의 후보인 frontier points 의 개수입니다. k 의 3 배 정도로 설정하였습니다.

initialize(query, buffer_size) 함수는 buffer_size 개만큼의 random seeds 를 선택한 다음, 그 점들과 query points 간의 거리를 계산하는 함수입니다. 이 함수는 뒤에서 구현합니다.

최대 max_steps 만큼 network 를 이동하며 frontier points 를 업데이트 합니다. Column vector 형태인 numpy.ndarray 는 numpy.concatenate 를 이용하여 붙일 수 있습니다. 이 merged column vector 에 numpy.unique 를 적용하면 중복된 값은 제거됩니다. 앞서 random neighbors 를 만들 때, 혹시라도 중복된 점들이 선택되더라도 이 과정에서 안전하게 제거됩니다. 이를 candi_idxs 라 하였습니다.

concatenate 하는 점들은 이전 step 에서 frontier points 로 선택된 idxs 와 이 idxs 의 random & nearest neighbors 입니다. Neighbor points 를 가져오는 함수 _get_neighbors() 는 이후에 구현합니다.

X[candi_idxs] 로 reference data 를 slicing 을 하여 query point 와의 pairwise distance 를 계산합니다. 이 값 역시 column vector 로 만들기 위하여 reshape(-1) 을 하였습니다.

그 뒤에는 most_closest_points() 함수를 구현할 때처럼 argsort 를 이용하여 현재의 candi_idxs 중에서 query point 와 가장 가까운 buffer_size 개의 점을 frontier points (idxs_) 로 선택합니다.

Frontier points 가 업데이트 되었는지는 dist 의 average 값이 변하였는지를 확인함으로써 해결합니다. 이 diff 값을 출력하면 수렴 속도를 확인할 수 있습니다.

class NetworkBasedNeighbors:
    ...

    def search_neighbors(self, query, k=5, max_steps=10, converge=0.000001):
        buffer_size = self.buffer_factor * k
        dist, idxs = self._initialize(query, buffer_size)

        for step in range(max_steps):
            candi_idxs = np.unique(
                np.concatenate([idxs, self._get_neighbors(idxs)])
            )

            candi_dist = pairwise_distances(
                query, self.X[candi_idxs], metric=self.metric).reshape(-1)

            args = candi_dist.argsort()[:buffer_size]
            idxs_ = candi_idxs[args]
            dist_ = candi_dist[args]
            dist_avg_ = dist_.sum() / dist_.shape[0]

            diff = dist_avg - dist_avg_
            if diff <= converge:
                break

            dist = dist_
            idxs = idxs_
            dist_avg = dist_avg_

        idxs_ = dist.argsort()[:k]
        idxs = idxs[idxs_]
        dist = dist[idxs_]

        return dist, idxs, infos, process_time

앞서 언급한 _initialize() 함수를 구현합니다. numpy.random.randint() 함수를 이용하여 buffer_size 개의 integer 인 idxs 를 만듭니다. 이 역시 중복된 점이 포함되어도 괜찮습니다. 이후에 np.unique 를 이용하여 제거할 것이기 때문입니다.

임의로 선택된 점들 (refx)과 query point 와의 pairwise distance 를 계산하여 dist 에 저장합니다. 이들 (dist, idxs) 을 return 합니다.

class NetworkBasedNeighbors:
    ...

    def _initialize(self, query, buffer_size):
        idxs = np.random.randint(self.n_data, size=buffer_size)
        refx = self.X[idxs]
        dist = pairwise_distances(refx, query)
        return dist, idxs

base 들의 random & nearest neighbors 를 가져오는 _get_neighbors(base) 함수를 구현합니다.

Random 과 nearest neighbors 의 index 는 각각 self.rn, self.nn 에 있습니다. 이들을 가져온 뒤, column vector 로 만들기 위하여 reshape(-1) 을 합니다. 이 값을 numpy.concatenate() 를 이용하여 하나의 column vector로 만들어 return 합니다.

class NetworkBasedNeighbors:
    ...

    def _get_neighbors(self, base):
        neighbor_idxs = np.concatenate(
            [self.nn[base].reshape(-1),
             self.rn[base].reshape(-1)]
        )
        return neighbor_idxs

Usage

앞서 설명한 코드는 verbose mode 를 제외한 코드입니다. 작동 과정을 살펴보기 위해 몇 개의 verbose 를 넣어둔 구현체를 github에 올려두었습니다. API 는 같으니 올려둔 구현체를 기준으로 demo 를 만들어봅니다.

실험에 이용할 20 차원의 100,000 개의 인공데이터를 만듭니다.

import numpy as np
from network_based_nearest_neighbors import NetworkBasedNeighbors

x = np.random.random_sample((100000, 20))

class instance 를 만들면서 동시에 indexing 을 합니다. 아래의 값은 default vaule 입니다. 이는 사용자에 의하여 조절 가능합니다.

index = NetworkBasedNeighbors(
    x,                     # reference data. numpy.ndarray or scipy.sparse.csr_matrix
    n_nearest_neighbors=5, # number of nearest neighbors
    n_random_neighbors=5,  # number of random neighbors
    batch_size=500,        # indexing batch size
    metric='euclidean',    # metric, possible all metric defined in scipy
    verbose=True           # verbose mode if True
)

Verbose mode 에서는 batch_size 에 의하여 나뉘어진 mini batch 의 계산 현황과 남은 시간이 출력됩니다. Indexing 이 끝난 뒤에는 indexing 계산 시간이 출력됩니다.

Indexing ...
batch 50 / 50 done. computation time = 1370.529929 sec.
Indexing was done

현재 indexing 시간이 오래 걸리는 이유는 nearest neighbor graph 를 만들기 위하여 brute-force 로 모든 pairwise distance 를 계산하기 때문입니다. 이 부분은 NN-descent 와 같은 더 빠른 nearest neighbor graph constructor 로 대체해야 합니다.

search 에는 a query vector 를 입력하도록 되어 있습니다. Column 이 아닌 a row 가 입력되어야 sklearn.metric.pairwise_distances 를 이용할 수 있습니다. Sample 로 0 번째 row 를 reshape(1, -1) 을 이용하여 a row vector 로 만들었습니다.

search_neighbors(query, k) 함수를 이용하면 dist, idxs 만 출력됩니다.

query = x[0].reshape(1,-1)
k = 10

dist, idxs = index.search_neighbors(query, k=k)

search_neighbors() 함수는 _search_neighbors_dev() 함수를 호출한 뒤, dist, idxs 만 선택하여 return 하는 함수입니다.

_search_neighbors_dev(query, k) 함수는 network 를 이용하여 탐색되는 점들의 업데이트 과정을 살펴보기 위한 함수입니다.

dist, idxs, infos, process_time = index._search_neighbors_dev(query, k=k)

infos 는 frontier points 를 업데이트하는 매 step 의 평균 거리와 이전 step 과의 거리차이가 저장된 list 입니다.

계산 시간은 process_time 에 저장되어 있습니다. 단위는 초 입니다.

# dist
array([2.98023224e-08, 2.85201523e-01, 2.95597815e-01, 3.36564885e-01,
       3.56957804e-01, 3.70693699e-01, 3.74081769e-01, 3.74408702e-01,
       3.87436487e-01, 4.00869548e-01]),

# idxs
 array([    0, 59013, 71981,  2622, 70642, 24061, 13159, 88382, 83117,
        15864]),

# infos
 [(0, 0.8117015629564891, 0.410979860874393),
  (1, 0.649891623106027, 0.1618099398504621),
  (2, 0.5649134791311035, 0.08497814397492354),
  (3, 0.46662289235625853, 0.09829058677484492),
  (4, 0.40744066573492627, 0.05918222662133227),
  (5, 0.4000953222237806, 0.0073453435111456855),
  (6, 0.4000953222237806, 0.0)],

# process_time [secs]
 0.0019750595092773438)

Small-world phenomenon

Small-world phenomenon 은 Stanley Milgram 의 6 단계 분리 이론 실험으로 널리 알려진 network 의 특징입니다. 이 실험은 임의의 어떤 사람 (query point) 에게 편지를 한 통 씁니다. 그 다음, 나의 친구 k 명에게 “이 편지를 받아야 하는 사람 (query point)을 알 것 같은 사람”에게 이 편지를 전해주라고 부탁합니다. 편지를 부탁 받은 사람들은 편지를 k 개로 복사하여 자신의 다른 k 명의 친구에게 똑같은 부탁을 합니다. 편지가 전달된다면 그 경로에 몇 명의 사람의 손을 거쳐 전달이 되었는지를 확인합니다. 그 결과 미국 내에서 임의의 사람에게 편지가 전해지는데 평균 6 단계가 걸린다는 실험입니다.

사실 친구의 친구라면 최대 $k + k^2$ 명의 사람에게 이를 물어본 것과 같습니다. 그 친구까지 고려하면 살펴볼 친구는 매우 많아집니다. 그런데 부탁을 받은 사람들은 자신의 친구들 중 임의의 k 명이 아닌, “편지를 받는 사람을 알 것 같은 사람 (query point 와 더 가까워질 수 있는 사람)”을 선택합니다. 이 과정은 우리가 살펴본 알고리즘에서 nearest & random neighbors 중에서 query point 와 더 가까운 p 개의 frontier points 를 선택하는 과정입니다.

만약 nearest neighbor graph 만 이용하였다면 아주 먼 initial points 가 선택되면 조금밖에 query point 와 가까워지지 않습니다. 그러나 random neighbors 를 연결해두었기 때문에 “편지를 받을 사람을 매우 잘 알 것 같은 의외의 인맥”에게 편지를 부탁할 수 있게 됩니다.

하지만 random neighbor graph 만을 이용하면 query point 와 어느 정도 가까워졌을 경우, 정말로 가까운 이웃을 모를 수도 있습니다.

즉, random neighbor graph 는 전체 공간을 종횡으로 횡단하며 query point 와 가까운 아주 큰 지역을 이동합니다. 그리고 query point 근처에 도착하면 nearest neighbor graph 에 의하여 조금씩 더 가까이 이동합니다. 이는 마치 “서울시 관악구” 까지는 빠르게 이동한 뒤, 관악구 내에서는 천천히 이동하며 편지를 받을 사람을 찾아가는 것과 같습니다.

그리고 기하급수적으로 탐색 영역이 넓어지기 때문에 neighbor networks 가 매우 이상하게 꼬이지 않는다면, 대체로 탐색 횟수 (num steps)는 비슷합니다. 즉, 임의의 query point 에 대하여 안정적인 탐색 속도를 보여준다는 의미입니다.

위 데이터의 2,000 개의 sample queries 에 대하여 search time 과 search steps 를 확인합니다. max stems 는 20 으로 설정하였습니다.

대부분은 7 ~ 12 번 사이에 탐색이 됩니다. 이 횟수는 nearest & random neighbors 의 개수에 따라 달라집니다. 한 step 에 여러 개의 이웃을 살펴본다면 steps 의 횟수는 조금 줄어듭니다. 하지만 그만큼 index 가 많은 정보를 저장하고 있어야 합니다.

num steps	num case
6	35
7	157
8	380
9	443
10	369
11	267
12	154
13	98
14	36
15	28
16	16
17	4
18	8
19	3
20	2

시간도 0.001 ~ 0.002 사이에 대부분 몰려 있습니다.

search time [secs]	percentage
0.001015 ~ 0.001292	7.75 %
0.001292 ~ 0.001569	34.45 %
0.001569 ~ 0.001846	23.30 %
0.001846 ~ 0.002122	17.65 %
0.002122 ~ 0.002399	9.90 %
0.002399 ~ 0.002676	3.05 %
0.002676 ~ 0.002953	1.65 %
0.002953 ~ 0.003230	0.70 %
0.003230 ~ 0.003506	0.60 %
0.003506 ~ 0.003783	0.35 %
0.003783 ~ 0.004060	0.10 %

실제로 100,000 개의 reference data 에 대하여 full pairwise distance 의 계산과 sorting 을 하였을 경우 평균 0.027 초의 시간이 걸립니다. 대략 15 ~ 25 배 정도 빠른 nearest neighbor search 가 이뤄집니다.

from sklearn.metrics import pairwise_distances
import time

k = 10
t = time.time()

dist = pairwise_distances(query, x).reshape(-1)
idxs = dist.argsort()[:k]
dist = dist[idxs]
t = time.time() - t

물론 성능은 정확하지는 않습니다. 하지만, distance 를 확인하면 큰 차이가 나지 않습니다. 더 주목해야 하는 점은, (이 포스트에서는 다루지 않았지만) 데이터의 개수가 10 배 늘어난다 하여도 network 를 이용한 탐색 시간은 10 배로 늘어나지 않습니다. 이웃의 이웃의 이웃을 한 단계만 더 살펴보아도 10 배 이상의 이웃을 살펴볼 수 있기 때문입니다. 즉, 데이터의 크기의 증가분에 따라 탐색 비용이 선형으로 증가하지 않습니다. 하지만 full pairwise distance computation 은 정직하게 데이터의 크기만큼 계산 시간이 늘어납니다.

Related posts

잠깐 언급된 NN-descent 는 neighbor search 를 위한 index 는 아닙니다. 주어진 reference data, X 에 대하여 X 간의 (approximated) k-nearest neighbor graph 를 빠르게 찾기 위한 방법입니다. 그리고 이 알고리즘의 작동 원리도 small-world phenomenon 입니다. 이에 대해서는 이후에 다른 포스트에서 다루도록 하겠습니다.