From Softmax Regression to Conditional Random Field for Sequential Labeling

Conditional Random Field (CRF) 는 sequential labeling 문제에서 Recurrent Neural Network (RNN) 등의 deep learning 계열 알고리즘이 이용되기 이전에 널리 사용되던 알고리즘입니다. Conditional Random Field 는 Softmax regression 의 일종입니다. 그러나 a vector point 가 아닌, sequence 형식의 입력 변수에 대하여 같은 길이의 label sequence 를 출력합니다. 이를 위해서 Conditional Random Field 는 potential function 을 이용합니다. Potential function 은 다양한 형식의 sequence data 를 high dimensional Boolean sparse vector 로 변환하여 입력 데이터를 logistic regression 이 처리할 수 있도록 도와줍니다. 이번 포스트에서 다룰 내용은 Softmax regression 과 Conditional Random Field 와의 관계와 potential function 입니다. 더하여 Conditional Random Field 와 같은 문제를 풀기 위해 이용되던 Maximum Entropy Markov Model 에 대해서도 알아봅니다.

Brief review of Logistic (Softmax) regression

Conditional Random Field (CRF) 는 softmax regression 입니다. 정확히는 categorical sequential data 를 softmax regression 이 이용할 수 있는 형태로 변형한 뒤, 이를 이용하여 sequence vector 를 예측하는 softmax regression 입니다. 그렇기 때문에 softmax regression 에 대하여 간략히 리뷰합니다.

Logistic 은 $(X, Y)$ 가 주어졌을 때, feature $X$ 와 $Y$ 와의 관계를 학습합니다. 특히 $Y$ 가 positive / negative 와 같이 두 개의 클래스로 이뤄져 있을 때 이용하는 방법입니다. Logistic 은 positive, negative 클래스에 속할 확률을 각각 계산합니다. Exponential 의 값은 nonnegative 이기 때문에 모든 경우에 대하여 $exp(\theta_i^Tx)$ 의 값을 더하여, 이 값으로 각각의 $exp(\theta_i^Tx)$ 를 나눠주면 확률 형식이 됩니다.

$$\begin{bmatrix} P(y=1~\vert~x) \\ \cdots \\ P(y=n~\vert~x) \end{bmatrix} = \begin{bmatrix} \frac{exp(\theta_1^Tx)}{\sum_k exp(\theta_k^Tx)} \\ \cdots \\ \frac{exp(\theta_n^Tx)}{\sum_k exp(\theta_k^Tx)} \end{bmatrix}$$

Logistic regression 을 기하학적으로 해석할 수도 있습니다. 각각의 $\theta$ 는 일종의 클래스의 대표벡터가 됩니다. $\theta_1$ 은 파란색 점들을 대표하는 백터, $\theta_2$ 는 빨간색 점들을 대표하는 벡터입니다. 하나의 클래스 당 하나의 대표벡터를 가집니다. 만약 한 점 $x$ 가 $\theta_1$ 과 일치한다면 $exp(\theta_1^Tx)$ 는 어느 정도 큰 양수가, $exp(\theta_2^Tx)$ 는 0에 가까운 값이 되기 때문에 $x$ 의 클래스 1에 해당할 확률이 1이 됩니다. Logistic regression 은 각 점에 대하여 각 클래스의 대표벡터에 얼마나 가까운지를 학습하는 것입니다.

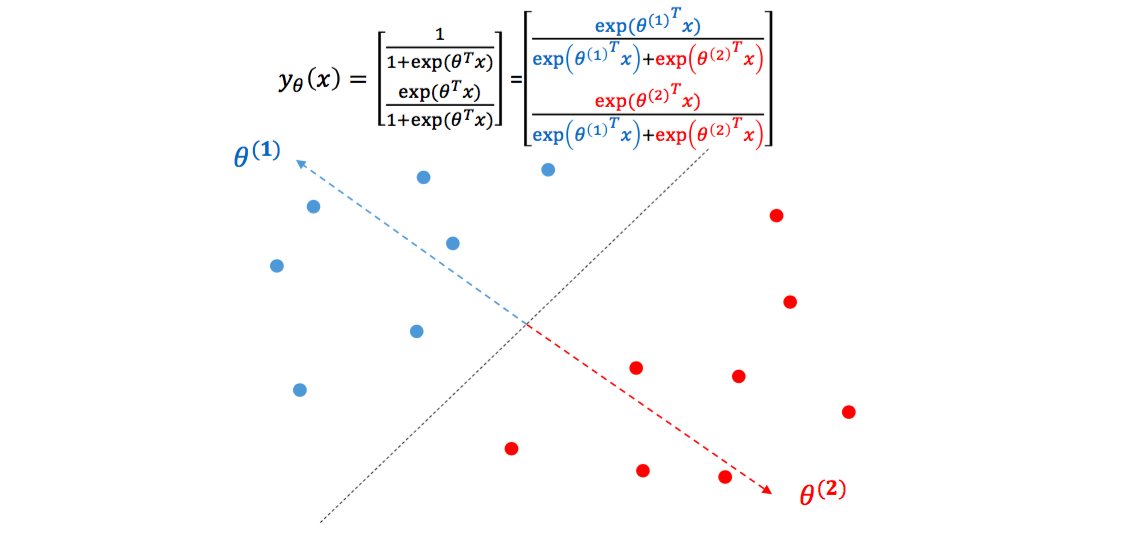
Softmax regression 은 logistic regression 의 일반화버전입니다. 클래스가 2 보다 많은 $n$ 개일 때, $n$ 개의 의 대표벡터를 학습하는 것입니다. 각 클래스를 구분하는 결정단면은 대표벡터의 Voronoi diagram 과 같습니다. 단, 각 대표벡터에 얼마나 가까운지는 벡터 간 내적 (inner product) 로 정의됩니다.

$$\begin{bmatrix} P(y=1~\vert~x) \\ \cdots \\ P(y=n~\vert~x) \end{bmatrix} = \begin{bmatrix} \frac{exp(-\theta_1^Tx)}{\sum_k exp(-\theta_k^Tx)} \\ \cdots \\ \frac{exp(-\theta_n^Tx)}{\sum_k exp(-\theta_k^Tx)} \end{bmatrix}$$

우리는 인공데이터를 만들어서 softmax regression 의 특징을 좀 더 살펴보겠습니다. 데이터 생성 파일은 링크로 올려두었습니다. 총 5 개의 클래스에 대하여 각 클래스 별로 100 개의 2 차원 데이터를 만들었습니다. Softmax regression 으로 각 클래스의 $\theta$ 를 학습하며 star marker 로 표현합니다.

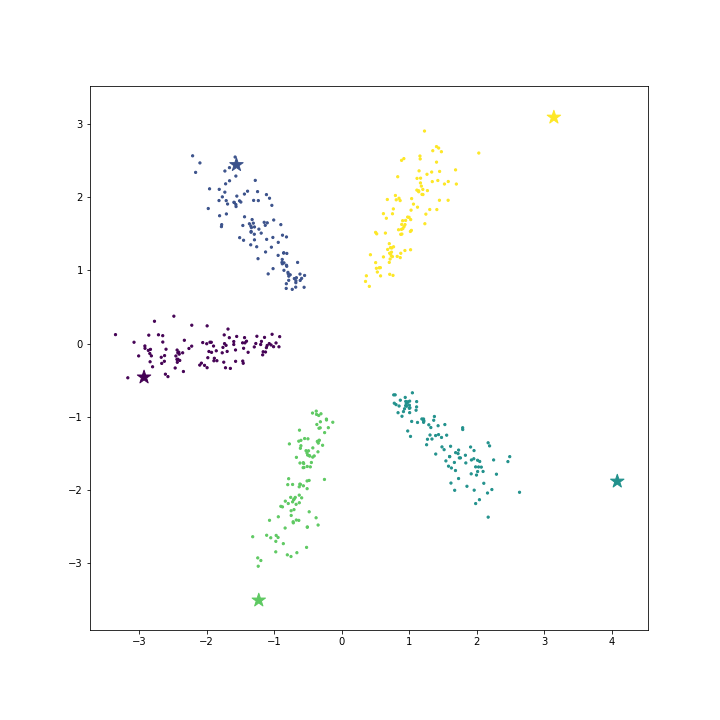
예시는 우리가 이해할 수 있는 2 차원의 scatter plot 이지만, 비슷한 현상은 고차원 벡터 공간에서도 일어납니다. 각 클래스의 대표벡터를 학습합니다.

Sequential labeling

일반적으로 classification 이라 하면, 하나의 입력 벡터 $x$ 에 대하여 하나의 label 값 $y$ 를 return 하는 과정입니다. 그런데 입력되는 $x$ 가 벡터가 아닌 sequence 일 경우가 있습니다. $x$ 를 길이가 $n$ 인 sequence, $x = [x_1, x_2, \ldots, x_n]$ 라 할 때, 같은 길이의 $y = [y_1, y_2, \ldots, y_n]$ 을 출력해야 하는 경우가 있습니다. Labeling 은 출력 가능한 label 중에서 적절한 것을 선택하는 것이기 때문에 classification 입니다. 데이터의 형식이 벡터가 아닌 sequence 이기 때문에 sequential data 에 대한 classification 이라는 의미로 sequential labeling 이라 부릅니다.

띄어쓰기 문제나 품사 판별이 대표적인 sequential labeling 입니다. 품사 판별은 주어진 단어열 $x$ 에 대하여 품사열 $y$ 를 출력합니다.

• $x = [이것, 은, 예문, 이다]$ .
• $y = [명사, 조사, 명사, 조사]$ .

띄어쓰기는 길이가 $n$ 인 글자열에 대하여 [띈다, 안띈다] 중 하나로 이뤄진 Boolean sequence $y$ 를 출력합니다.

• $x = 이것은예문입니다$ .
• $y = [0, 0, 1, 0, 1, 0, 0, 1]$ .

이 과정을 확률모형으로 표현하면 주어진 $x$ 에 대하여 $P(y \vert x)$ 가 가장 큰 $y$ 를 찾는 문제입니다. 이를 아래처럼 기술하기도 합니다. $x_{1:n}$ 은 길이가 $n$ 인 sequence 라는 의미입니다.

$$argmax_y P(y_{1:n} \vert x_{1:n})$$

위 문제를 풀 수 있는 가장 간단한 방법 중 하나는 각각의 $y_i$ 에 대하여 독립적인 labeling 을 수행하는 것입니다. ‘너’라는 글자에 대하여 학습데이터에서 가장 많이 등장한 품사를 출력합니다. 하지만 한 단어는 여러 개의 품사를 지닐 수 있습니다. 한국어의 ‘이’라는 단어는 tooth, two 라는 의미의 명사일 수도 있고, 조사나 지시사일 수도 있습니다. 문맥을 고려하지 않으면 모호성이 발생합니다.

더 좋은 방법은 앞, 뒤 단어와 품사 정보들을 모두 활용하는 것입니다. ‘너’라는 단어 앞, 뒤의 단어와 우리가 이미 예측한 앞 단어의 품사를 이용한다면 더 정확한 품사 판별을 할 수 있습니다. 특히 앞 단어의 품사를 이용하면 문법적인 비문을 방지할 수 있습니다. 예를 들어 ‘조사’ 다음에는 ‘조사’가 등장하기 어렵습니다. 앞에 조사가 등장하였다면, 이번 단어의 품사가 조사일 가능성은 낮도록 유도할 수 있습니다.

Sequential labeling using Softmax regression

앞에서 이야기한 개념을 logistic regression 을 이용하여 구현할 수 있습니다. 길이가 $n$ 인 $x = [x_1, x_2, \ldots, x_n]$ 에 대하여 $y = [y_1, y_2, \ldots, y_n]$ 을 출력하기 위하여 $n$ 개의 독립적인 classification 을 수행합니다. 이 classifier 는 모든 경우에 공유되는 하나의 classifier 입니다.

$y_1$ 을 예측하는데는 $x_1$ 을 이용합니다. $y_2$ 를 예측하는데는 $x_1$, $x_2$, 그리고 앞서 예측한 $y_1$ 을 이용합니다. 이 과정을 일반적으로 기술하면 다음과 같습니다.

• $y_1 = f(x_1)$ .
• $y_2 = f(x_1, x_2, y_1)$ .
• $\ldots$ .
• $y_n = f(x_{n-1}, x_n, y_{n-1})$ .

이를 정리하면 길이가 $n$ 인 $x_{1:n}$ 에 대하여 $y_{1:n}$ 이 출력될 확률은 아래처럼 기술할 수 있습니다. $P(y_1 \vert x_{1:n})$ 은 $y_1$ 예측하는데 $x_{1:n}$ 의 어떤 부분을 이용해도 좋다는 의미입니다. 이 말 안에는 $x_1$ 을 이용하여 $y_1$ 을 예측하는 부분이 포함됩니다.

$$P(y_{1:n} \vert x_{1:n}) = P(y_1 \vert x_{1:n}) \times \left( \prod_{i=2:n} P(y_i \vert x_{1:n}, y_{i-1}) \right)$$

모든 경우에 대하여 $y_i$ 를 출력할 수 있는 하나의 classifiers 를 학습하여 길이가 $n$ 인 sequence 에 대해 순차적으로 $n$ 번 적용하면 sequential labeling 을 할 수 있습니다. 이 때 classifier 로 softmax regression 이 이용될 수 있습니다.

Maximum Entropy Markov Model (MEMM)

이런 방식으로 sequential labeling 을 하는 모델을 Maximum Entropy Markov Model (MEMM) 이라 합니다. Hidden Markov Model (HMM) 에서 우리가 관찰할 수 있는 데이터 $x$ 를 observation 이라 하며, 이 observation 이 발생할 조건, 즉 label $y$ 를 state 라 합니다.

식 $y_n = f(x_{n-1}, x_n, y_{n-1})$ 에서 현재 시점 $y_i$ 의 state 를 판단하는데 이용되는 다른 state 는 이전 시점 $y_{i-1}$ 뿐입니다. 이처럼 현재 시점의 state 에 영향을 줄 수 있는 다른 state 가 과거의 state 일 때 이를 Markov model 이라 합니다.

Maximum Entropy Model 은 softmax regression 형식의 classifier 를 의미합니다. 아래는 softmax regression 의 각 클래스에 속할 확률값입니다.

$$\begin{bmatrix} P(y=1~\vert~x) \\ \cdots \\ P(y=n~\vert~x) \end{bmatrix} = \begin{bmatrix} \frac{exp(-\theta_1^Tx)}{\sum_k exp(-\theta_k^Tx)} \\ \cdots \\ \frac{exp(-\theta_n^Tx)}{\sum_k exp(-\theta_k^Tx)} \end{bmatrix}$$

이를 기반으로 softmax regression 의 loss function 은 다음처럼 기술됩니다. 아래 식은 cross entropy 입니다. Softmax regression 은 $\theta$ 에 의한 예측값과 정답데이터의 cross entropy 를 최소화합니다.

$$loss = -\left( \sum_{i=1}^{m} \sum_{k=1}^{n} 1 \left( y^{(i)}=k \right) log \frac{exp(\theta^k \cdot x^{(i)})}{\sum_{j=1}^{n} exp(\theta^j \cdot x^{(i)})} \right)$$

그런데 minimum entropy model 이 아닌 maximum entropy model 이란 이름이 붙은 배경은 다음과 같습니다. 위의 loss function 은 학습데이터에 등장한 패턴에 대한 식입니다. 모델이 예측하는 확률과 데이터에 등장하는 패턴의 확률이 일치할수록 cross entropy 는 작아집니다. 하지만 학습데이터에 등장하지 않은 단어의 품사를 판단하는 것처럼 모르는 input 에 대해서는 일절의 판단을 할 수 없습니다. 확률로 표현하면 모든 label 에 대한 확률이 uniform 이어야 하는데, 이 때 entropy 가 최대가 됩니다. 아래는 maximum entropy model 의 이름의 유래에 대한 CMU 튜토리얼의 원문입니다.

Intuitively, the principle is simple: model all that is known and assume nothing about that which is unknown. In other words, given a collection of facts, choose a model which is consistent with all the facts, but otherwise as uniform as possible. This is precisely the approach we took in selecting our model tex2html_wrap_inline1520 at each step in the above example.

Reference: http://www.cs.cmu.edu/afs/cs/user/aberger/www/html/tutorial/node2.html

Maximum entropy model 에 대한 더 자세한 설명은 CMU 의 튜토리얼과 ratsgo 님의 블로그를 보시기 바랍니다.

Maximum Entropy Markov Model 은 softmax regression 과 같은 방식으로 labeling 을 하면서, sequential data 의 특징을 반영하기 위하여 Markov Model 의 구조를 이용합니다. 그렇기 때문에 이와 같은 이름이 붙여졌습니다.

MEMM 의 $P(y_{1:n} \vert x_{1:n})$ 은 다음처럼 기술됩니다.

$$P(y \vert x) = \prod_{i=1}^{n} \frac{exp(\sum_{j=1}^{m} \lambda_j f_j (x, i, y_i, y_{i-1}))}{ \sum_{y^{`}} exp(\sum_{j^{`}=1}^{m} \lambda_j f_j (x, i, y_i^{`}, y_{i-1}^{`})) }$$

$f_j$ 는 potential function 입니다. Potential functions 에 의하여 $m$ 차원의 sparse vector 로 표현된 $x_i$와 coefficient vector $\lambda$ 의 내적에 exponential 이 취해집니다. 다른 labels 후보 $y^{`}$ 의 값들의 합으로 나뉘어집니다. Softmax regression 형식입니다. 정확히는 Maximum Entropy Model 입니다. 그리고 이 과정이 $n$ 번 반복됩니다.

Potential function

그런데 softmax regression 은 벡터 $x$ 에 대하여 label $y$ 를 출력하는 함수입니다. 이를 위해서는 식 $f(x_{i-1}, x_i, y_{i-1})$ 에 들어가는 입력변수를 벡터로 표현해야 합니다. Potential function 은 단어와 같은 categorical value 를 포함하여 sequence 로 입력된 다양한 형태의 값을 벡터로 변환합니다.

임의 형태의 값이라도 벡터로 표현할 수 있는 방법 중 하나는 그 값이 내가 원하는 경우인지를 Boolean 으로 표현하는 필터를 이용하는 것입니다.

Numerical sequence

예를 들어 $x = [3.2, 2.1, -0.5]$ 라는 길이가 3 인 sequence 에 대하여 아래의 필터 $F_1$ 를 적용할 수 있습니다.

• $x = [3.2, 2.1, -0.5]$ .
• $F_1 = 1$ if $x_i > 0$ else $0$
• $x_{vec} = [1, 1, 0]$ .

필터를 여러 개 이용할 수도 있습니다. 각 시점 $i$ 에 대한 벡터의 크기는 필터의 개수와 같습니다.

• $x = [3.2, 2.1, -0.5]$ .
• $F_1 = 1$ if $x_i > 0$ else $0$
• $F_2 = 1$ if $x_i > 3$ else $0$
• $x_{vec} = [(1, 1), (1, 0), (0, 0)]$ .

Part of speech tagging

이 필터가 potential function 입니다. Potential function 은 categorical variable 에 대해서도 적용이 가능합니다.

• $x = [이것, 은, 예문, 이다]$ .
• $F_1 = 1$ if $x_{i-1} =$ ‘이것’ & $x_i =$ ‘은’ else $0$
• $F_2 = 1$ if $x_{i-1} =$ ‘이것’ & $x_i =$ ‘예문’ else $0$
• $F_3 = 1$ if $x_{i-1} =$ ‘은’ & $x_i =$ ‘예문’ else $0$
• $x_{vec} = [(0, 0, 0), (1, 0, 0), (0, 0, 1), (0, 0, 0)]$ .

앞서 달아둔 label $y_{i-1}$ 를 함께 이용하기 위한 potential function 도 만들 수 있습니다.

• $x = [이것, 은, 예문, 이다]$ .
• $F_1 = 1$ if $x_{i-1} =$ ‘이것’ & $x_i =$ ‘은’ else $0$
• $F_2 = 1$ if $x_{i-1} =$ ‘이것’ & $x_i =$ ‘예문’ else $0$
• $F_3 = 1$ if $x_{i-1} =$ ‘은’ & $x_i =$ ‘예문’ else $0$
• $F_4 = 1$ if $x_{i-1} =$ ‘이것’ & $x_i =$ ‘은’ & $y_{i-1} =$ ‘명사’ else $0$
• $F_5 = 1$ if $x_{i-1} =$ ‘이것’ & $x_i =$ ‘예문’ & $y_{i-1} =$ ‘명사’ else $0$
• $F_6 = 1$ if $x_{i-1} =$ ‘은’ & $x_i =$ ‘예문’ & $y_{i-1} =$ ‘조사’ else $0$

우리가 $i=1$ 까지 [명사, 조사]로 labels 을 달아뒀다면 $x_{vec}(i=2)$ 는 다음과 같은 벡터를 지닐 겁니다.

• $x = [이것, 은, 예문, 이다]$ .
• $y = [명사, 조사, ?, ?]$ .
• $x_{vec}(i=2) = (0, 0, 1, 0, 0, 1)$ .

Potential function 은 사용자가 설계하기 나름입니다. 우리가 앞 시점의 단어와 품사, 그리고 현재 시점의 단어만을 고려하는 potential function 을 이용했을 뿐입니다. $i-2$ 나 $i+2$ 시점의 단어를 확인할 수도 있으며, 심지어 문장의 길이나 문장에 특정 단어가 포함되었는지를 확인할 수도 있습니다.

Character level spacing

우리는 다음 포스트에서 한국어 띄어쓰기 교정기를 직접 만들 겁니다. 띄어쓰기 문제를 위한 potential function 에 대해서 이야기합니다.

아래는 두 어절로 이뤄진 문장, “예문 입니다” 입니다. 앞의 품사 판별의 예시처럼 앞글자와 앞글자의 띄어쓰기 예측값, 그리고 현재 글자만을 이용한다고 가정하면 다음과 같은 potential functions 을 이용할 수 있습니다.

• $x = '예문 입니다'$ .
• $F_1 = 1$ if $x_{i-1:i} =$ ‘예문’ else $0$
• $F_2 = 1$ if $x_{i-1:i} =$ ‘예문’ & $y[i-1] = 0$ else $0$
• $F_3 = 1$ if $x_{i-1:i} =$ ‘문입’ else $0$
• $$\cdots$$

그런데 우리가 직접 앞글자와 현재 글자를 모두 파악한 뒤 이를 potential function 으로 만들기는 어렵습니다. 그 종류가 어마어마 합니다. 대신 구현을 할 때에는 templates 를 입력합니다. 위처럼 앞글자와 태그, 그리고 현재 글자를 이용하는 template 을 다음처럼 표현할 수 있습니다. 이번에는 현재 시점을 $i$ 가 아닌 $0$ 이라 표현하였습니다.

• templates
  • $x_{-1:0}$ .
  • $x_{-1:0}$ & $y_{-1}$ .

아래 그림은 위 “예문 입니다” 의 예제에 대하여 템플릿을 적용한 결과입니다. 우리는 길이가 5 인 문장에 대하여 5 번의 (마지막 글자는 반드시 띄기 때문에 정확히는 4번 입니다) classification 을 하여야 합니다.

이 때 각 classification 에 이용할 수 있는 features 는 potential functions 에 의하여 만들어집니다. Potential functions 에 의하여 1 의 값을 받는 features 의 개수는 매우 작습니다. Potential function 은 현재 시점이 특정한 경우인가를 판단하는 필터이기 때문입니다. 그 결과 한 시점에 대한 벡터는 대부분의 값이 0 인 sparse vector 이며, 0 이 아닌 값들은 Boolean filter 의 결과로 1 을 지닙니다.

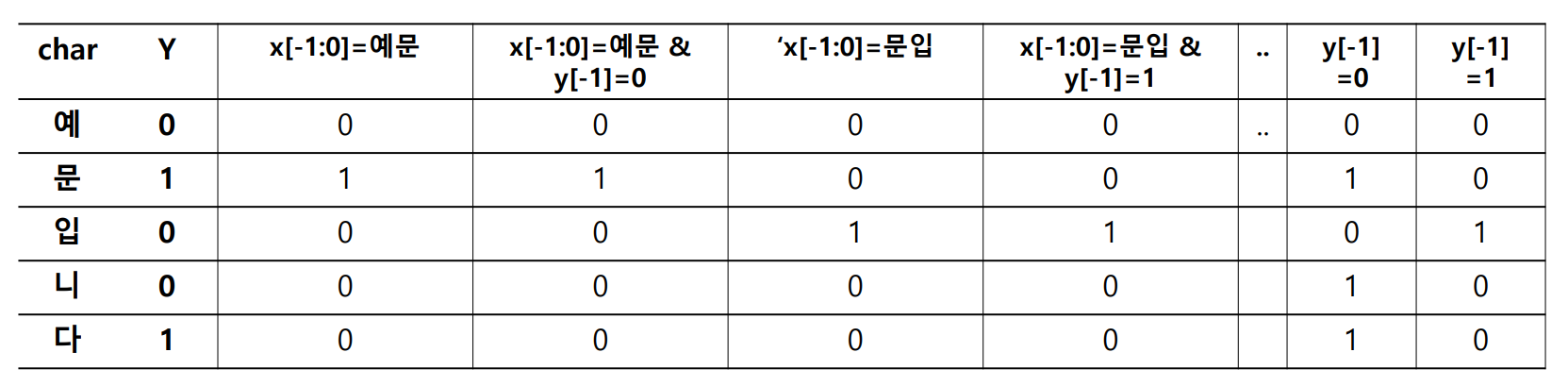
이는 마치 5 개의 문서에 대한 term frequency vector 처럼 보이기도 합니다. Potential functions 에 의하여 feature vector 로 변형된 $x_i$ 는 이제 maximum entropy model (softmax regression) 에 입력되어 classification 이 됩니다.

Label bias

Maximum Entropy Markov Model 의 식은 설득력이 있습니다.

$$P(y_{1:n} \vert x_{1:n}) = P(y_1 \vert x_{1:n}) \times \left( \prod_{i=2:n} P(y_i \vert x_{1:n}, y_{i-1}) \right)$$

그러나 위 식처럼 sequentially labeling 을 수행하면 label bias 라는 현상이 발생합니다. 아래 그림은 일본어 형태소 분석기 MeCab 논문의 예시 그림입니다.

Reference: Kudo et al., 2014

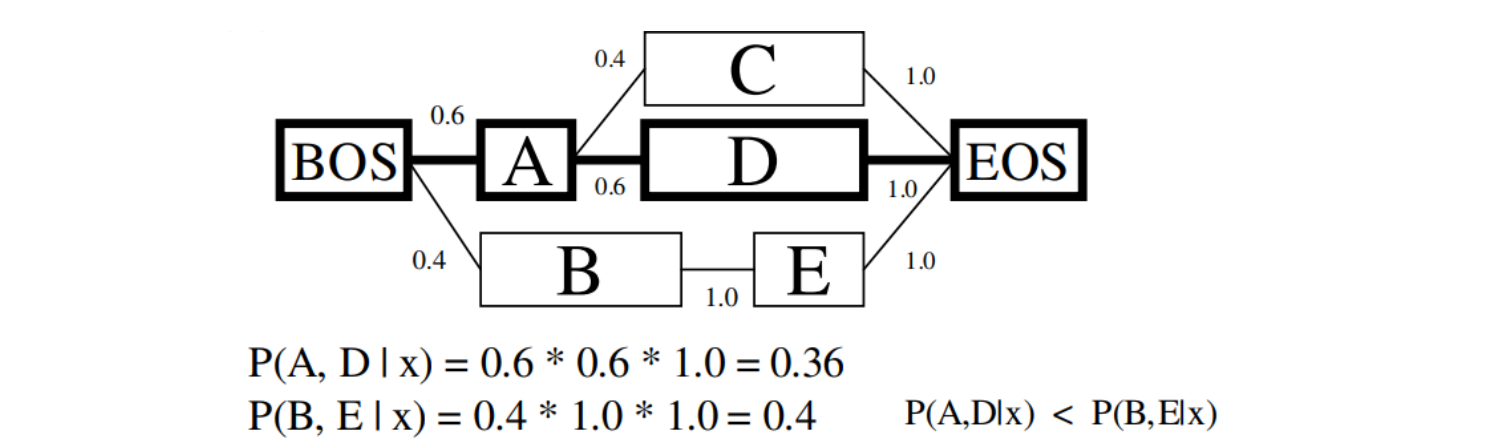
입력된 데이터 $x$ 의 실제 정답은 $y = [A, D]$ 였습니다. $A$ 가 자주 등장한 state 라면 이후 다른 states 들이 여러 가지 등장할 수 있습니다. 아래 그림에서는 $C$ 와 $D$ 가 $A$ 다음에 등장하였습니다. $A$ 가 frequent 하여 다른 states 로 넘어갈 때의 확률이 분할됩니다.

하지만 infrequent state 였던 $B$ 는 언제나 $E$ 앞에 등장하였습니다. $B$ 가 state 로 이용된 적이 적어서 $P(B \rightarrow E)$ 가 높을 뿐인데, 오히려 왜곡이 생깁니다. 그 결과 $P(A, D \vert x) < P(B, E \vert x)$ 여서 잘못된 labeling 이 이뤄집니다.

From Maximum Entropy Markov Model to Conditional Random Field

Label bias 의 원인은 Markov Model 이 전체 그림을 보지 않고 지엽적인 정보만을 이용했기 때문입니다. Conditional Random Field 는 이 문제를 해결하기 위해 제안됩니다. 실제로 MEMM 은 ICML 2000 에, CRF 는 ICML 2001 에서 발표됩니다. 두 논문 모두 McCallum 와 Pereira 가 저자입니다.

CRF 와 MEMM 의 차이는 $n$ 번의 순차적인 classifications 를 수행하느냐, a sequence 에 대한 한 번의 classification 을 수행하느냐 입니다. 물론 states 의 개수가 $k$ 개라면 후보는 $k^n$ 개를 만들 수 있지만, 애초에 가능성이 적은 후보들도 많습니다. 불필요한 후보는 만들지 않고 몇 개의 후보를 만든 뒤, 각각의 label sequence 에 대한 정답 확률을 계산합니다.

MEMM 의 $P(y_{1:n} \vert x_{1:n})$ 은 다음처럼 기술되었습니다.

$$P(y \vert x) = \prod_{i=1}^{n} \frac{exp(\sum_{j=1}^{m} \lambda_j f_j (x, i, y_i, y_{i-1}))}{ \sum_{y^{`}} exp(\sum_{j^{`}=1}^{m} \lambda_j f_j (x, i, y_i^{`}, y_{i-1}^{`})) }$$

$f_j$ 는 potential function 입니다. Potential functions 에 의하여 $m$ 차원의 sparse vector 로 표현된 $x_i$와 coefficient vector $\lambda$ 의 내적에 exponential 이 취해집니다. 다른 labels 후보 $y^{`}$ 의 값들의 합으로 나뉘어집니다. Softmax regression 형식입니다. 그리고 이 과정이 $n$ 번 반복됩니다.

CRF 의 $P(y_{1:n} \vert x_{1:n})$ 은 다음처럼 기술됩니다.

$$P(y \vert x) = \frac{exp(\sum_{j=1}^{m} \sum_{i=1}^{n} \lambda_j f_j (x, i, y_i, y_{i-1}))}{ \sum_{y^{`}} exp(\sum_{j^{`}=1}^{m} \sum_{i=1}^{n} \lambda_j f_j (x, i, y_i^{`}, y_{i-1}^{`})) }$$

이 역시도 Maximum Entropy Model 입니다. 그리고 CRF 에서 이전 state 정보만을 이용하는 경우를 linear-chain CRF 라 합니다. 다양한 시점의 states 를 모두 이용하면 그만큼 potential functions 의 개수만 많아집니다.

이 개념은 아래의 그림처럼 표현할 수도 있습니다. MEMM 은 입력된 sequence data $x$ 에 대하여 앞부분부터 적절한 labels 을 찾아갑니다. 하지만 CRF 는 가능성이 있는 sequence $y$ 후보를 몇 개 선택한 뒤, 가장 적합한 하나의 label 을 고릅니다.

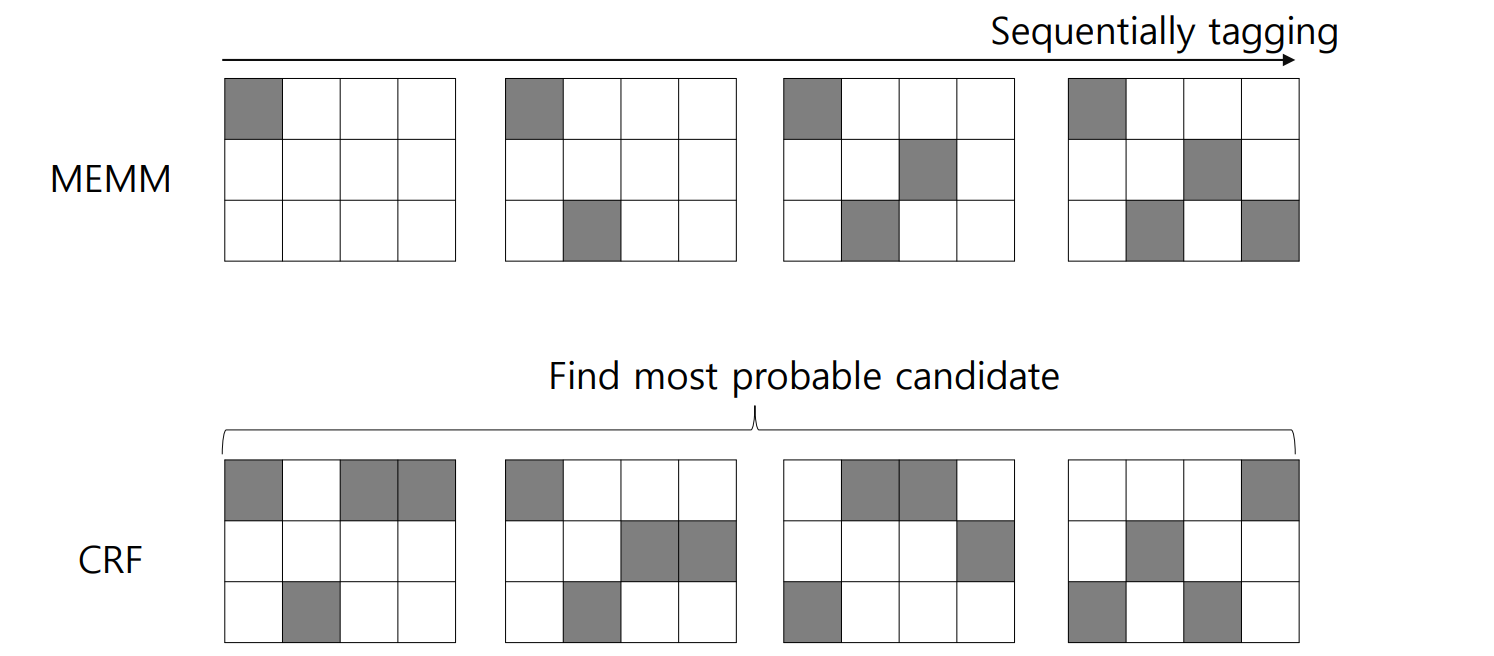
Conclusion

Conditional Random Field 는 sequence data $x$ 에 가장 적합한 sequence response $y$ 를 찾는 classifier 입니다.

입력 데이터의 형태는 숫자, 단어, 패턴 등 다양합니다. 이들을 softmax regression 이 이용할 수 있도록 벡터로 변환하기 위하여 potential functions 이 이용됩니다. Potential functions 은 sequence data 를 sequence of high dimensional sparse vector 로 변환합니다.

Maximum Entropy Markov Model 은 Conditional Random Field 와 비슷한 방식으로 작동합니다. 하지만 MEMM 은 label bias 문제가 발생합니다. CRF 는 이를 해결하기 위하여 제안된 방법입니다.

Read more

crfsuite 는 Conditional Random Field 를 C 로 구현한 소프트웨어입니다. pycrfsuite 는 이를 Python 에서 이용할 수 있도록 도와주는 패키지 입니다. 우리는 다음 포스트에서 pycrfsuite 를 이용한 한국어 띄어쓰기 알고리즘을 직접 만들어봅니다.

이 과정에서 pycrfsuite package 를 이용할 때 주의해야 하는 점들도 함께 논의합니다.

References

• Kudo, T., Yamamoto, K., & Matsumoto, Y. (2004). Applying conditional random fields to Japanese morphological analysis. In Proceedings of the 2004 EMNLP
• Lafferty, J., McCallum, A., & Pereira, F. C. (2001). Conditional random fields: Probabilistic models for segmenting and labeling sequence data.
• McCallum, A., Freitag, D., & Pereira, F. C. (2000, June). Maximum Entropy Markov Models for Information Extraction and Segmentation. In Icml (Vol. 17, pp. 591-598)
• ratsgo’s blog