Spherical k-means for document clustering

k-means 는 빠르고 값싼 메모리 비용 때문에 대량의 문서 군집화에 적합한 방법입니다. scikit-learn 의 k-means 는 Euclidean distance 를 이용합니다. 그러나 고차원 벡터인 문서 군집화 과정에서는 문서 간 거리 척도의 정의가 매우 중요합니다. Bag-of-words model 처럼 sparse vector 로 표현되는 고차원 데이터에 대해서는 Euclidean distance 보다 Cosine distance 를 사용하는 것이 좋습니다. 그리고 Cosine distance 를 이용하는 k-means 를 Spherical k-means 라 합니다. 이번 포스트에서는 왜 문서 군집화에 Cosine distance 를 이용해야 하는지에 대하여 알아보고, Spherical k-means + fast initializer + clustering labeling 기능을 제공하는 패키지에 대해 알아봅니다.

k-means

k-means 는 다른 군집화 알고리즘과 비교하여 매우 적은 계산 비용을 요구하면서도 안정적인 성능을 보입니다. 그렇기 때문에 큰 규모의 데이터 군집화에 적합합니다. 문서 군집화의 경우에는 문서의 개수가 수만건에서 수천만건 정도 되는 경우가 많기 때문에 다른 알고리즘보다도 k-means 가 더 많이 선호됩니다. k-partition problem 은 데이터를 k 개의 겹치지 않은 부분데이터 (partition)로 분할하는 문제 입니다. 이 때 나뉘어지는 k 개의 partiton 에 대하여, “같은 partition 에 속한 데이터 간에는 서로 비슷하며, 서로 다른 partition 에 속한 데이터 간에는 이질적”이도록 만드는 것이 군집화라 생각할 수 있습니다. k-means problem 은 각 군집 (partition)의 평균 벡터와 각 군집에 속한 데이터 간의 거리 제곱의 합 (분산, variance)이 최소가 되는 partition 을 찾는 문제입니다.

$\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}$

우리가 흔히 말하는 k-means 알고리즘은 Lloyd 에 의하여 제안되었습니다. 이는 다음의 순서로 이뤄져 있습니다.

k 개의 군집 대표 벡터 (centroids) 를 데이터의 임의의 k 개의 점으로 선택합니다.
모든 점에 대하여 가장 가까운 centroid 를 찾아 cluster label 을 부여하고,
같은 cluster label 을 지닌 데이터들의 평균 벡터를 구하여 centroid 를 업데이트 합니다.
Step 2 - 3 의 과정을 label 의 변화가 없을때까지 반복합니다.

우리가 list of str 형태의 문서 집합을 가지고 있을 때, scikit-learn 을 이용하여 k-means 를 학습하는 방법은 매우 간단합니다. 아래의 코드는 문서 집합을 bag-of-words model 로 표현한 다음 k-means 를 적용하는 과정까지의 코드입니다.

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.preprocessing import normalize
from sklearn.cluster import KMeans

docs = ['document format', 'list of str like']

# vectorizing
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(docs)

# training k-means
kmeans = KMeans(n_clusters=k).fit(X)

# trained labels and cluster centers
labels = kmeans.labels_
centers = kmeans.cluster_centers_

Spherical k-means for sparse vector clustering

위 코드의 scikit-learn k-means 는 Euclidean distance 를 이용하여 문서 간 거리를 정의합니다. 하지만 bag-of-words model 처럼 sparse vector 로 표현되는 고차원 데이터 간의 거리를 정의하기에 Euclidean distance 는 적합하지 않습니다. Euclidean distance 는 벡터의 크기에 영향을 받기 때문입니다.

Euclidean distance 를 이용한 두 벡터 $v_1, v_2$ 의 거리는 아래처럼 정의됩니다. 두 벡터의 L2 norm 의 합에서 두 벡터의 내적의 두 배를 뺀 값으로, 두 벡터 간의 거리에 크기가 영향을 미칩니다.

$d_{euc}(v_1, v_2) = \sqrt{v_1^2 + v_2^2 - 2 \cdot v_1 \cdot v_2}$

아래 그림은 세 문서의 예시입니다. 문서 1 과 문서 3 은 사용된 단어의 종류와 비율이 같지만, 문서 3 이 단어의 개수가 2 배씩 많습니다. 문서 1 과 3 의 L2 norm 크기는 $\sqrt{3}$ 과 $\sqrt{6}$ 이며, 문서 1 과 3의 Euclidean distance 또한 $\sqrt{3}$ 입니다. 그런데 문서 1 과 문서 2 의 Euclidean distance 역시 $\sqrt{3}$ 으로 같습니다. 문서 1 과 3 은 벡터의 크기에 의하여 길이가 생겼고, 문서 1 과 2 는 사용된 단어 분포가 달라서 길이가 생겼습니다.

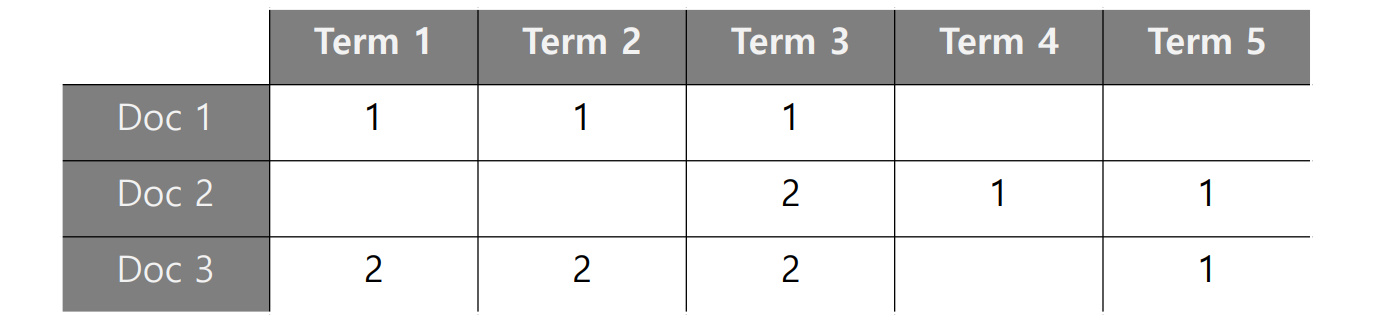
사람은 단어 분포가 비슷할 때 두 문서가 topically similar 하다고 생각합니다. Cosine distance 를 이용하면 문서 1 과 3 의 거리는 0 입니다. 이 둘은 단어의 분포가 같기 때문입니다. 좀 더 자세히 살펴보면 Cosine similarity 는 아래처럼 두 벡터의 내적을 두 벡터의 L2 norm 으로 나눈 값이며, Cosine distance 는 1 - Cosine similarity 입니다. 이는 두 벡터를 unit vector 화 시킨 뒤 내적하는 것과 같습니다. 모든 벡터의 크기가 무시됩니다. 그리고 내적을 하기 때문에 두 벡터에 공통으로 들어있는 단어들이 무엇인지, 그리고 그 비율이 얼만큼이 되는지를 측정합니다.

$d_{cos}(v_1, v_2) = 1 - \frac{v_1 \cdot v_2}{\vert v_1 \vert \vert v_2 \vert}$

이러한 내용은 (Anna Huang, 2008) 에서도 언급됩니다. 이 논문에서는 고차원의 sparse vectors 간의 거리 척도는 두 벡터에 포함된 공통 성분의 무엇인지를 측정하는 것이 중요하기 때문에 Jaccard distance, Pearson correlation, Cosine distance 와 같은 척도를 쓰면 거리가 잘 정의되나, Euclidean distance 를 이용하면 안된다고 말합니다.

Cosine distance 를 이용하면 모든 벡터가 unit vector 화 되기 떄문에 k-means 군집화는 아래 그림처럼 각도가 비슷한 (단어 분포가 비슷한) 문서를 하나의 군집으로 묶는 의미로 해석할 수 있습니다. 이처럼 sparse vector 로 표현되는 문서 집합에 대한 k-means 는 Cosine distance 를 이용하는 것이 좋고, Cosine distance 를 이용하는 k-means 를 Spherical k-means 라 합니다 (Inderjit et al., 2001).

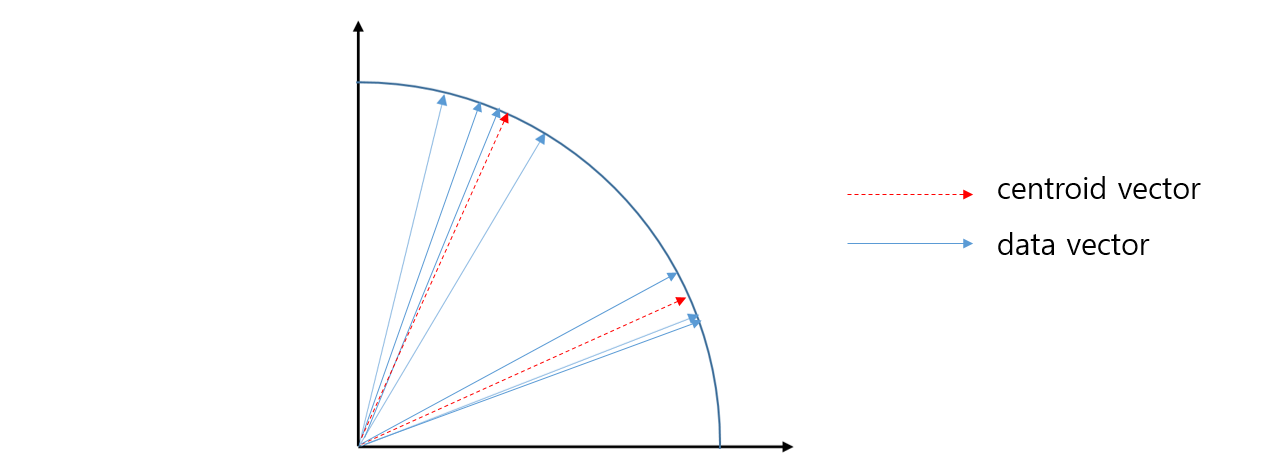
만약 사용하는 k-means 가 Euclidean distance 를 이용하고 있다면 두 가지만 변경하여 k-means 를 Spherical k-means 로 손쉽게 바꿀 수 있습니다. 첫째는 input 으로 입력되는 행렬 x 의 모든 rows 를 unit vectors 로 만드는 것입니다. 둘째, centroid update 를 할 때, 한 군집에 포함된 모든 벡터의 합을 rows 의 개수로 나누는 것이 아니라, 벡터의 합을 L2 normalize 하여 centroid 를 unit vector 로 만드는 것입니다. Lloyd k-means 처럼 한 군집 안의 벡터의 합을 rows 의 개수로 나누는 것은 L1 normalize 의 효과가 있으며, centroid 의 크기가 1 이라는 보장이 없습니다. 그렇기 때문에 다음 번 반복 계산에서 모든 rows 와 centroids 간의 거리를 계산할 때 군집의 centroid vector 의 크기에 영향을 받게 됩니다. 이렇게 두 경우만 바꾸면 Euclidean distance 를 이용하는 것과 Cosine distance 를 이용하는 것이 동일한 학습 결과를 가집니다. 모든 벡터의 크기가 1 이라면 Euclidean distance 기준으로 가장 가까운 벡터는 벡터의 내적이 가장 큰 (Cosine similarity 가 가장 큰) 벡터이기 때문입니다.

import numpy as np
from sklean.preprocessing import normalize

class KMeans:
    def __init__(self, n_clusters, max_iters...):
        self.n_clusters = n_clusters
        self.max_iters = max_iters
        ...

    def fit(self, x):
        x = normalize(x, norm='l2')
        self.cluster_center_ = np.zeros((self.n_clusters, x.shape[1]))
        for iter_ in range(self.max_iters):
           ...
           self._centroid_update(x, labels)
           ...

    def _centroid_update(self, x, labels):
        for c in range(self.n_clusters):
            idxs = np.where(labels == c)[0]
            x_cluster = x[idxs,:]
            #k-means
            #self.cluster_center_[c,:] = x_cluster.sum(axis=0) / idxs.shape[0]
            
            #spherical k-means
            self.cluster_center_[c,:] = normalize(x_cluster.sum(axis=0), norm='l2')
            ...

이전에 k-means 의 initializer 를 다루는 포스터에서 고차원 sparse vectors 간에는 대부분의 Cosine distance 가 1 에 가깝기 때문에, 일반적으로 이용되는 k-means++ 과 같은 initializer 는 많은 계산 비용만 들 뿐, 어떠한 효과도 없는 (비싼 random sampling) 방법이라는 말을 하였습니다.

또한 bag-of-words model 로 표현된 문서 집합을 k-means 로 학습하면 데이터 기반으로 군집의 레이블을 부여할 수 있다는 내용도 clustering labeling 포스트에서 언급하였습니다.

위 두 관련 블로그의 내용은 아래의 soyclustering 패키지에 구현되어 있습니다.

Packages

initializer, labeler, 그리고 오늘 이야기한 Spherical k-means 까지 포함하여 코드를 구현하였습니다. 이는 github 에 올려두었습니다. 아래는 패키지 사용법입니다.

https://github.com/lovit/clustering4docs

k-means 는 매우 빠르게 수렴하기 때문에 max_iter 를 크게 잡을 필요가 전혀 없습니다. 오히려 n_clusters 를 크게 잡아야 합니다. 이 내용에 대해서는 이후에 k 를 결정하는 방법에 대한 다른 포스트에서 자세히 다룹니다. init 은 initializer 의 이름입니다. ‘similar_cut’ 은 앞서 언급한 initializer 의 가제입니다.

from soyclustering import SphericalKMeans
spherical_kmeans = SphericalKMeans(
    n_clusters=1000,
    max_iter=10,
    verbose=1,
    init='similar_cut'
)

labels = spherical_kmeans.fit_predict(x)

verbose = 1 로 설정하면 매 반복 마다 label 이 변하는 rows 의 개수, 군집 내 rows 간의 pairwise distance 의 합, 걸리는 학습 시간과 centroid vector 의 sparsity가 출력됩니다. 아래 데이터는 30,091 개의 문서 집합에 대한 군집화 과정입니다. 실제로 10 번의 반복만으로도 거의 수렴함을 알 수 있습니다. 80 개 정도 labels 이 흔들리는 것들은 수렴되지 않은 것이 아니라, uniform effect 같은 과적합 현상일 수 있습니다. Uniform effect 에 대해서도 이후에 다른 포스트에서 다루겠습니다.

initialization_time=1.218108 sec, sparsity=0.00796
n_iter=1, changed=29969, inertia=15323.440, iter_time=4.435 sec, sparsity=0.116
n_iter=2, changed=5062, inertia=11127.620, iter_time=4.466 sec, sparsity=0.108
n_iter=3, changed=2179, inertia=10675.314, iter_time=4.463 sec, sparsity=0.105
n_iter=4, changed=1040, inertia=10491.637, iter_time=4.449 sec, sparsity=0.103
n_iter=5, changed=487, inertia=10423.503, iter_time=4.437 sec, sparsity=0.103
n_iter=6, changed=297, inertia=10392.490, iter_time=4.483 sec, sparsity=0.102
n_iter=7, changed=178, inertia=10373.646, iter_time=4.442 sec, sparsity=0.102
n_iter=8, changed=119, inertia=10362.625, iter_time=4.449 sec, sparsity=0.102
n_iter=9, changed=78, inertia=10355.905, iter_time=4.438 sec, sparsity=0.102
n_iter=10, changed=80, inertia=10350.703, iter_time=4.452 sec, sparsity=0.102

군집화 결과를 이용하여 각 군집의 키워드를 추출하는 코드입니다.

from soyclustering import proportion_keywords

vocabs = [vocab for vocab, idx in sorted(vectorizer.vocabulary_.items(), key=lambda x:x[1])]
centers = kmeans.cluster_centers_

keywords = proportion_keywords(
    centers,
    labels=labels,
    index2word=vocabs)

122M 개의 문서로 이뤄진 IMDB reviews 입니다. k=1000 으로 설정하여 k-means 를 학습한 뒤, 위의 proportion keywords 함수를 이용하여 군집 레이블을 추출하였습니다. 아래는 5 개 군집의 예시입니다.

군집의 의미	키워드 (레이블)
영화 “타이타닉”	iceberg, zane, sinking, titanic, rose, winslet, camerons, 1997, leonardo, leo, ship, cameron, dicaprio, kate, tragedy, jack, di saster, james, romance, love, effects, special, story, people, best, ever, made
Marvle comics 의 heros (Avengers)	zemo, chadwick, boseman, bucky, panther, holland, cap, infinity, mcu, russo, civil, bvs, antman, winter, ultron, airport, ave ngers, marvel, captain, superheroes, soldier, stark, evans, america, iron, spiderman, downey, tony, superhero, heroes
Cover-field, District 9 등 외계인 관련 영화	skyline, jarrod, balfour, strause, invasion, independence, cloverfield, angeles, district, los, worlds, aliens, alien, la, budget, scifi, battle, cgi, day, effects, war, special, ending, bad, better, why, they, characters, their, people
살인자가 출연하는 공포 영화	gayheart, loretta, candyman, legends, urban, witt, campus, tara, reid, legend, alicia, englund, leto, rebecca, jared, scream, murders, slasher, helen, killer, student, college, students, teen, summer, cut, horror, final, sequel, scary
영화 “매트릭스”	neo, morpheus, neos, oracle, trinity, zion, architect, hacker, reloaded, revolutions, wachowski, fishburne, machines, agents, matrix, keanu, smith, reeves, agent, jesus, machine, computer, humans, fighting, fight, world, cool, real, special, effects

Reference

Anna Huang. Similarity measures for text document clustering. In Proceedings of the sixth new zealand computer science research 20 student conference (NZCSRSC2008), Christchurch, New Zealand, pages 49–56, 2008
Inderjit S Dhillon and Dharmendra S Modha. Concept decompositions for large sparse text data 120 using clustering. Machine learning, 42(1):143–175, 2001.
github.com/lovit/clustering4docs

k-means

Spherical k-means for sparse vector clustering

Related posts

Packages

Reference