Embedding for Word Visualization (LLE, ISOMAP, MDS, t-SNE)

머신 러닝의 많은 알고리즘들은 정보를 고차원 공간의 벡터 형태로 저장합니다. 이 공간은 수백 혹은 수십만 차원이 될 수 있기 때문에 공간을 그대로 이해하기 어렵습니다. 이러한 문제를 해결하기 위하여 고차원 공간을 2 차원으로 압축하여 시각화하는 임베딩 방법들이 이용될 수 있습니다. 이전 포스트에서 다뤘던 t-SNE 는 가장 많이 이용되는 벡터 시각화 임베딩 방법 중 하나입니다. t-SNE 이전에도 고차원 공간을 이해하기 위한 방법론들이 존재하였습니다. 이번 포스트에서는 이전에 대표적으로 이용되었던 Multi-Dimensional Scaling (MDS), Locally Linear Embedding (LLE), ISOMAP 에 대하여 알아봅니다. 더하여 위 세 알고리즘과 t-SNE 를 이용하여 term - document matrix 를 임베딩한 결과를 비교합니다.

Introduction

고차원의 벡터를 이해하기 위하여 시각화 방법들이 이용됩니다. 최근에는 안정적인 성능 때문에 t-Stochastic Neighbor Embedding (t-SNE) 가 가장 많이 이용되고 있습니다. t-SNE 는 2008 년도에 제안된 방법입니다. 그러나 오래전부터 고차원 공간을 시각적으로 이해하려는 시도가 있었습니다. 1964 년 제안되었던 Multi-Dimensional Scaling 은 무려 50 년 전에 제안된 임베딩 방법 중 하나입니다. 그리고 2000 년, Science 저널에 발표되었던 Locally Linear Embedding (LLE) 와 ISOMAP 은 nearest neighbors 정보를 이용하여 고차원 공간의 구조를 보존하는 저차원 공간을 학습하였습니다. 그 외에도 Principal Component Analysis (PCA) 와 이의 covariance matrix 를 kernel marix 로 대체한 kernel Principa Component Analysis (kPCA) 역시 고차원 공간의 시각화에 이용되었습니다. 사실 LLE 나 ISOMAP 은 deep learning 모델들의 임베딩 공간을 시각화 하기보다는 swissroll data 와 같이 manifold 가 존재하는 데이터 공간을 시각화 하는 데 적합합니다. 이번 포스트에서는 PCA, kPCA 를 제외한 MDS, LLE, ISOMAP, t-SNE 임베딩 알고리즘들이 각자 시각화 하려했던 정보가 무엇인지 비교해 봅니다.

고차원 공간의 벡터를 저차원으로 압축하여 시각화 할 때 중요한 정보는 가까이 위치한 점들 간의 구조입니다. 우리는 공간을 이해할 때 전체를 한 번에 인식하지 않습니다. 지구의 지도를 볼 때 특정한 지역에 집중합니다. 예를 들어 동아시아에서의 한국의 위치를 살펴본다면 한국의 우측에 일본이, 좌측에 서해를 사이에 둔 중국, 그리고 러시아 남부 일부가 눈에 들어옵니다. 이 때 우리는 한국과 인접한 정보들에 집중하며, 500 km 정도 떨어진 이 지역들이 한국을 중심으로 오른쪽에 있는지 왼쪽에 있는지가 중요합니다. 이 때, 남아메리카의 브라질이 한국과 얼마나 떨어져 있는지 아르헨티나가 얼마나 떨어지 있는지는 중요하지 않습니다. 둘 모두 대략 남서쪽 방향의 어딘가에 있다는 정보면 충분합니다. 그리고 유럽권 나라들은 서쪽 혹은 약간의 서북쪽 방향 어딘가에 있다는 정보면 충분합니다. 멀리 떨어진 점들의 정보는 디테일하게 집중할 필요가 없습니다. 하지만 locality 는 제대로 보존되어야 합니다. 이후 살펴볼 네 종류의 임베딩 알고리즘인 MDS, LLE, ISOMAP, t-SNE 을 이 관점에서 살펴보면 왜 t-SNE 가 고차원 벡터의 시각화 측면에서 안정적인 성능을 보이는지 이해할 수 있습니다.

Multi-Dimensional Scaling (MDS)

Multi-Dimensional Scaling (MDS) 는 1964 년에 제안된, 매우 오래된 임베딩 방법입니다. MDS 는 원 공간 $x$ 에서 모든 점들 간에 정의된 거리 행렬 $\delta$ 가 주어졌을 때, 임베딩 공간에서의 Euclidean distance 인 $\vert y_i - y_j \vert$ 와 거리 행렬 $\delta_{ij}$ 의 차이가 최소가 되는 임베딩 공간 $y$ 를 학습합니다. 학습 데이터가 원 공간의 벡터로 입력된다 하여도 $x$ 의 pairwise distance 를 계산함으로써 $\delta$ 를 만들 수 있습니다.

$minimize \sum_{i < j} \left( \vert y_i - y_j \vert - \delta_{ij} \right)^2$

MDS 는 모든 점들 간의 거리 정보를 보존합니다. 원 논문에서는 지역 간의 거리 정보를 input 으로 이용하여 지역의 위치를 복원하는 예시를 보여줍니다. 아래 그림의 좌측은 미국의 도시 간 거리이며, 우측은 이를 이용하여 MDS 를 학습한 결과입니다. 거리 행렬이 2 차원 좌표 값으로부터 계산된 정보이기 때문에 2 차원 지도가 복원되었음을 알 수 있습니다. 단, $y$ 공간은 임의의 방향으로 회전될 수 있습니다.

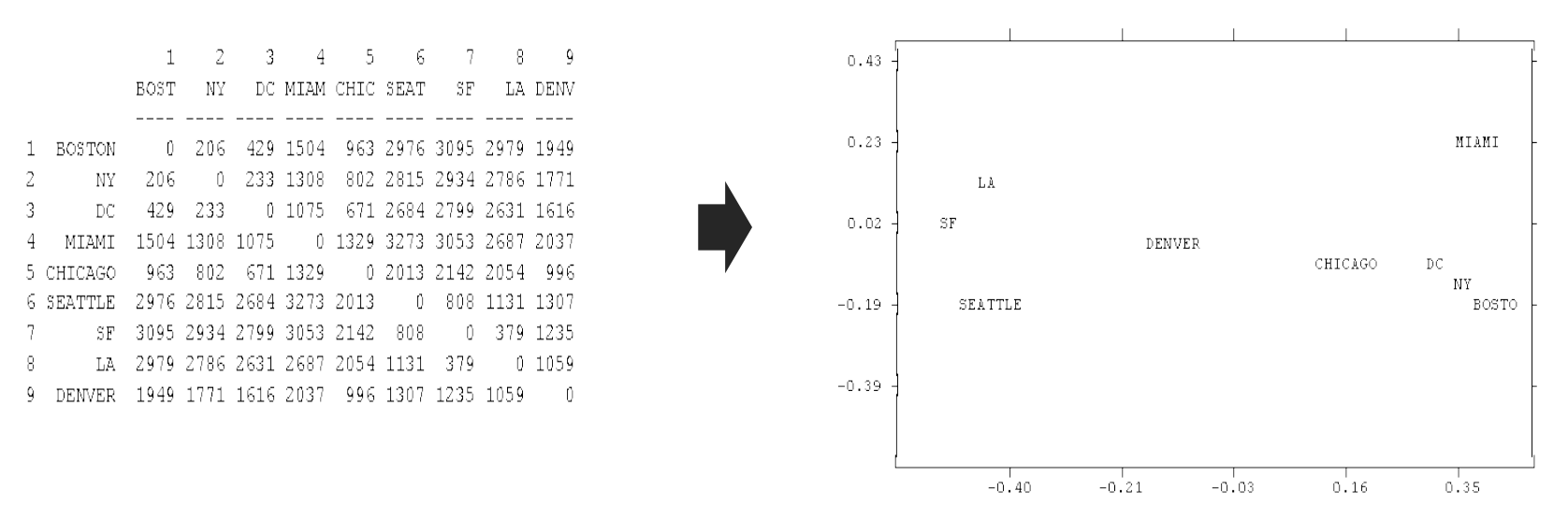
MDS 는 모든 점들 간의 거리 정보의 중요도가 같습니다. 그렇기 때문에 가까운 점들 간의 거리 정보보다 멀리 떨어진 점들 간의 거리 정보의 영향력이 큽니다. 10 만큼 떨어진 점들 간의 거리가 5 틀리는 것과 1000 만큼 떨어진 점들 간의 거리가 5 만큼 틀리는 것의 중요도는 다릅니다. 하지만 MDS 는 이 두 거리차를 동일하게 중요하다고 판단합니다. 그 결과 가까운 점들 간의 위치를 제대로 맞추는데 실패하게 됩니다. 고차원 공간에서의 거리는 가깝다라는 정보를 제외하면 대부분 차별성이 없는 무의미한 큰 값일 가능성이 높습니다. 하지만 MDS 는 무의미한 정보에 집중하여 고차원의 원 공간에서의 가까운 점들 간의 구조를 보존하지 못합니다. 그리고 고차원 벡터를 저차원으로 임베딩할 때에는 특정 모양의 결과를 학습합니다. 이에 대한 예시는 다음 장의 임베딩 방법 간의 비교에서 이야기 하겠습니다.

앞서 고차원 공간을 2 차원으로 시각화 하기 위해서는 locality 의 정보에 집중하는 것이 중요하다 언급하였습니다. 하지만 MDS 는 그와 반대의 정보에 집중합니다. 고차원 공간의 시각화에 적합한 방법이 아닙니다. 또한 MDS 는 metric space 를 가정합니다. 고차원 공간이 metric space 가 아니라면, 즉 (a, b), (a, c) 가 가까우나 (b, c) 가 멀다면 MDS 의 입장에서는 말이 되지 않는 공간입니다.

Scikit-learn 에서는 MDS 를 제공합니다. 사용법은 아래와 같습니다. scipy.sparse 가 입력되지 않습니다. Sparse matrix 는 x.todense() 함수를 이용하여 numpy.ndarray 로 형식을 변환해야 합니다.

from sklearn.manifold import MDS

y = MDS(n_components=2).fit_transform(x) # x: numpy.ndarray

Locally Linear Embedding (LLE)

2000 년, Science 저널에는 nearest neighbors 정보를 이용하는 임베딩 방법 두 가지가 출간되었습니다. 그 중 첫번째는 Locally Linear Embedding (LLE) 입니다. 이 방법은 MDS 와 다르게 원 공간에서의 최인접 이웃의 정보, locality 에 집중합니다. LLE 의 학습 과정은 아래 그림과 같습니다.

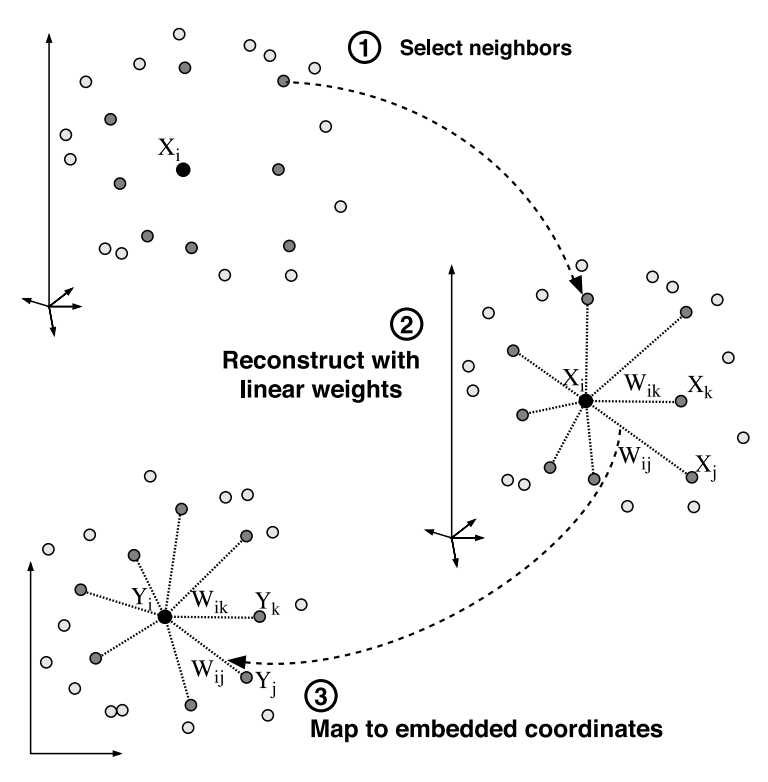
처음 원 공간 $x$ 에서 모든 점들에 대하여 k 개의 nearest neighbors 를 찾습니다 (이 과정이 생각보다 매우 비싼 계산 과정입니다). 두번째로 이웃 점들 간의 구조를 $w_{ij}$ 라는 패러매터로 학습합니다. 한 점 $x_i$ 는 nearest neighbors 인 $x_j$ 와 $w_ij$ 의 weights 로 선형결합이 될 수 있다 가정합니다. 마치 nearest neighbors 의 선형 결합으로 $x_i$ 를 복원하는 것과 같습니다.

$minimize \vert x_i - \sum_j w_{ij} \cdot x_j \vert^2$

여기서 학습되는 $w_ij$ 는 원 공간에서의 점들 간의 관계입니다. 이는 마치 원 공간에서 모든 점들이 nearest neighbors 와 손을 꼭 잡는 것과 같습니다. 그리고 이 손을 놓지 않고 2 차원 공간으로 내려올 것입니다. 이번에는 점들 간의 관계인 $w_{ij}$ 를 고정합니다. 이 정보를 가장 잘 유지할 수 있는 임베딩 공간 $y$ 를 학습합니다.

$minimize \vert y_i - \sum_j w_{ij} \cdot y_j \vert^2$

LLE 는 locality 만을 유지하며 임베딩 공간을 학습합니다. 하지만 이웃 정보만을 보존하여도 global structure 가 어느 정도 보존될 수 있습니다. 아래 그림은 LLE 논문에 기재된 사람의 얼굴 표정 사진을 임베딩한 결과입니다. 매우 많이 찡그린 얼굴 주변에는 찡그린 얼굴이 있고, 그 옆에는 덜 찡그린 얼굴이 있습니다. 조금씩 그 이웃의 이웃의 이웃을 살펴보면 어느 순간 조금 웃는, 그리고 더 많이 웃는 얼굴이 연속됩니다. 이웃 간의 구조를 보존하였더니 이웃의 이웃의 이웃으로 이동할 때 어떠한 정보가 한 축으로 학습될 수 있습니다.

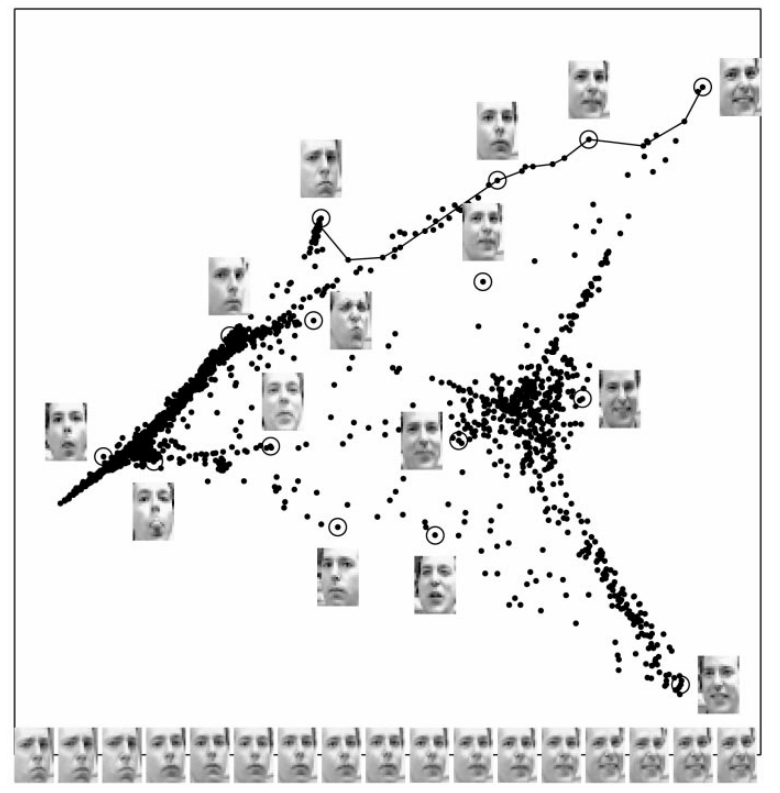
아래는 단어가 어떤 문서에 등장하였는지를 벡터로 나타낸 term - document matrix 를 LLE 를 이용하여 임베딩한 결과입니다. Term - document matrix 는 각 단어가 [(doc, weight), (doc, weight), … ] 형태로 표현된 벡터입니다. 비슷한 문서들에서 비슷한 비율로 등장한 단어들이라면 원 공간에서 비슷한 벡터를 지닙니다. 그리고 이 term - document matrix 를 임베딩하면 topically similar 한 두 단어는 비슷한 임베딩 벡터를 지닙니다. 실제로 아래 그림에서 killed, defeat, peace 와 같은 용어들이 비슷한 벡터로 학습되었음을 볼 수 있습니다.

Scikit-learn 은 LLE 를 제공합니다. 사용법은 아래와 같습니다. n_components 외에도 원 공간에서 이용하는 nearest neighbors 의 개수를 조절할 수 있습니다. 5 는 default value 입니다.

from sklearn.manifold import LocallyLinearEmbedding

y = LocallyLinearEmbedding(n_components=2, n_neighbors=5).fit_transform(x) # x: numpy.ndarray

LLE 는 MDS 와 다르게 locality 의 정보를 보존합니다. 그러나 locality 외에는 전혀 신경을 쓰지 않습니다. 그리고 nearest neighbors 의 값에 매우 민감하게 움직입니다. 이를 확인하기 위하여 한 가지 실험을 합니다. 이전 t-SNE 의 포스트에서 만들었던 데이터와 비슷합니다. 세 개의 군집 별로 50 개의 random samples 를 생성합니다.

import numpy as np

n_data_per_class = 50
n_classes = 3

x = []
y = []
for c in range(n_classes):
    x_ = 0.3 * np.random.random_sample((n_data_per_class, 2))
    x_ += np.random.random_sample((1, 2))
    x.append(x_)
    y.append(np.asarray([c] * n_data_per_class))
x = np.vstack(x)
y = np.concatenate(y)

Bokeh 를 이용하여 이 데이터를 scatter plot 으로 살펴봅니다. 반복적으로 scatter plot 을 그릴 것이니 draw_figure 라는 함수를 만들었습니다.

from bokeh.plotting import figure, show, output_notebook
from bokeh.layouts import gridplot
from bokeh.io import export_png

output_notebook()

title = '{} classes {} points'.format(n_classes, n_classes * n_data_per_class)

def draw_figure(x, y, title, show_figure=True,
    colors = 'firebrick darksalmon lightseagreen'.split()):

    p = figure(width=400, height=400, title=title)
    for c in range(n_classes):
        idx = np.where(y == c)[0]
        x_ = x[idx]
        p.scatter(x_[:,0], x_[:,1], fill_color=colors[c], line_color=colors[c])
    if show_figure:
        show(p)
    return p

p = draw_figure(x, y, title)

두 종류의 데이터는 어느 정도 붙어있으며, 주황색 데이터는 멀리 떨어진 형태입니다.

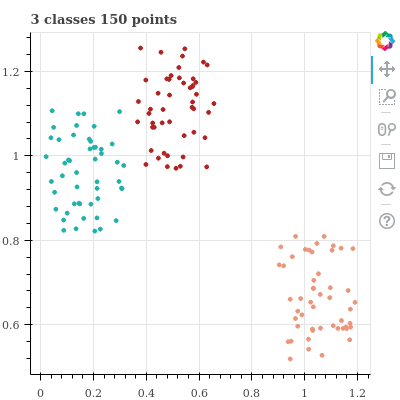
다양한 nearest neighbors (2, 3, 5, 10) 을 설정하여 LLE 를 학습합니다. Return 되는 figures 를 모아 gridplot 으로 그립니다.

from sklearn.manifold import LocallyLinearEmbedding

plots = []
for n_neighbors in [2, 3, 5, 10]:
    z = LocallyLinearEmbedding(
        n_components=2,
        n_neighbors=n_neighbors
    ).fit_transform(x)
    title = 'LLE with n_neighbors = {}'.format(n_neighbors)
    plots.append(draw_figure(z, y, title, show_figure=False))

gp = gridplot([[plots[0], plots[1]], [plots[2], plots[3]]])
show(gp)

Nearest neighbors 가 2 일 때에는 한 클래스 외에는 보이지 않습니다. 사실 두 클래스의 점들이 하나의 점으로 뭉쳐졌고, 에머럴드 색의 점들과 겹쳐서 보이지 않는 것입니다. Nearest neighbors = 3 일 때에는 세 클래스의 점들이 모두 보이지만, 각 클래스 별로 일자로 늘어선 것을 볼 수 있습니다. Nearest neighbors = 5 일 때와 10 일 때에는 멀리 떨어져있던 주황색 점들은 한 점으로 모이고, 다른 두 클래스는 일자로 늘어선 것을 볼 수 있습니다. 전혀 원 공간이 복원되지 않는 모습임을 알 수 있습니다.

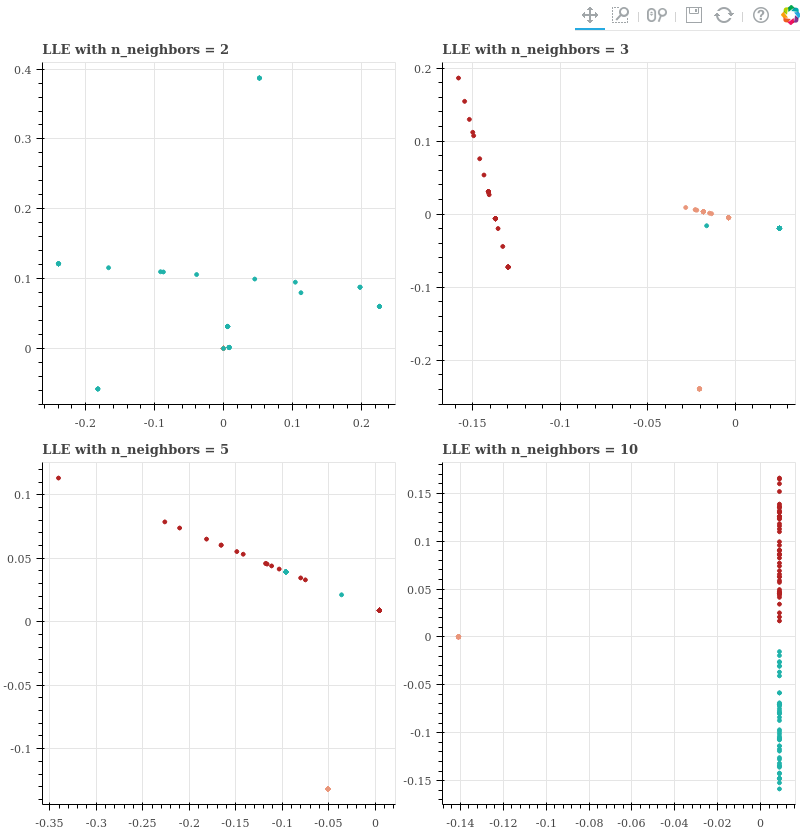
이런 패턴은 LLE 에서 자주 등장하는 패턴입니다. 사실 위의 사람 얼굴 예시에서도 이미지들이 어떤 선 모양을 그리며 늘어선 것을 볼 수 있습니다. 실제로 이러한 latent axis 는 존재하지 않음에도 말이죠.

ISOMAP

ISOMAP 은 LLE 처럼 원 공간 $x$ 에서 nearest neighbors graph 를 만든 다음, 이 그래프에서의 최단 경로 (shortest path) 로 점들 간의 거리를 정의합니다. 그리고 이 정보를 보존하는 임베딩 공간 $y$ 를 학습합니다.

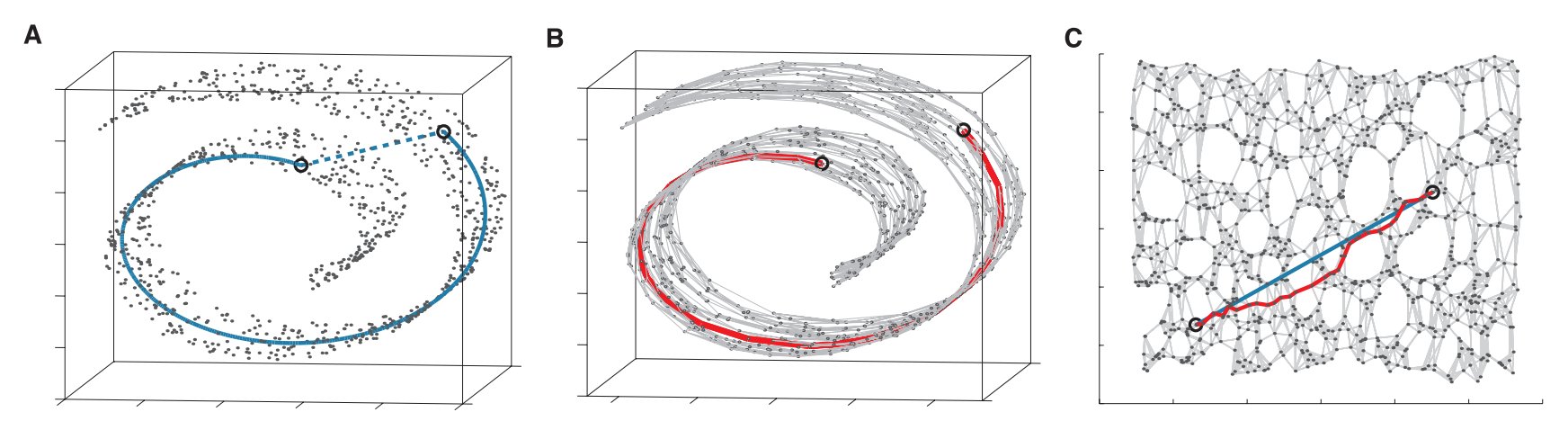
ISOMAP 의 동기는 아래 그림과 같습니다. 아래 그림의 (a) 처럼 3 차원에서의 두 점 간의 Euclidean distance 는 파란색의 직선으로 정의됩니다. 하지만 우리는 아래 그림의 공간은 ‘휘어진 띄’라고 인식합니다. 이 공간은 지구의 지표처럼 국소적으로는 평면과 같습니다. 우리는 한 도시 안에서의 두 점 사이의 거리를 Euclidean distance 로 정의합니다. 하지만 서울과 부에노스아이레스의 이동 거리는 Euclidean distance 로 정의할 수 없습니다. 지표를 따라 휘어진 곡면을 이동해야 하기 때문입니다. 이처럼 국소적으로는 평면이며 Euclidean distance 가 정의되는 공간을 manifold 라 합니다. ISOMAP 은 manifold 에서의 점들 간의 거리를 nearest neighbor graph 에서의 점들 간의 최단 경로로 정의합니다. 그림 (b) 처럼 표면을 따라 이동하는 거리로 두 점 사이의 거리를 정의합니다. 그리고 이 정보를 보존하는 2 차원 임베딩 공간을 학습합니다.

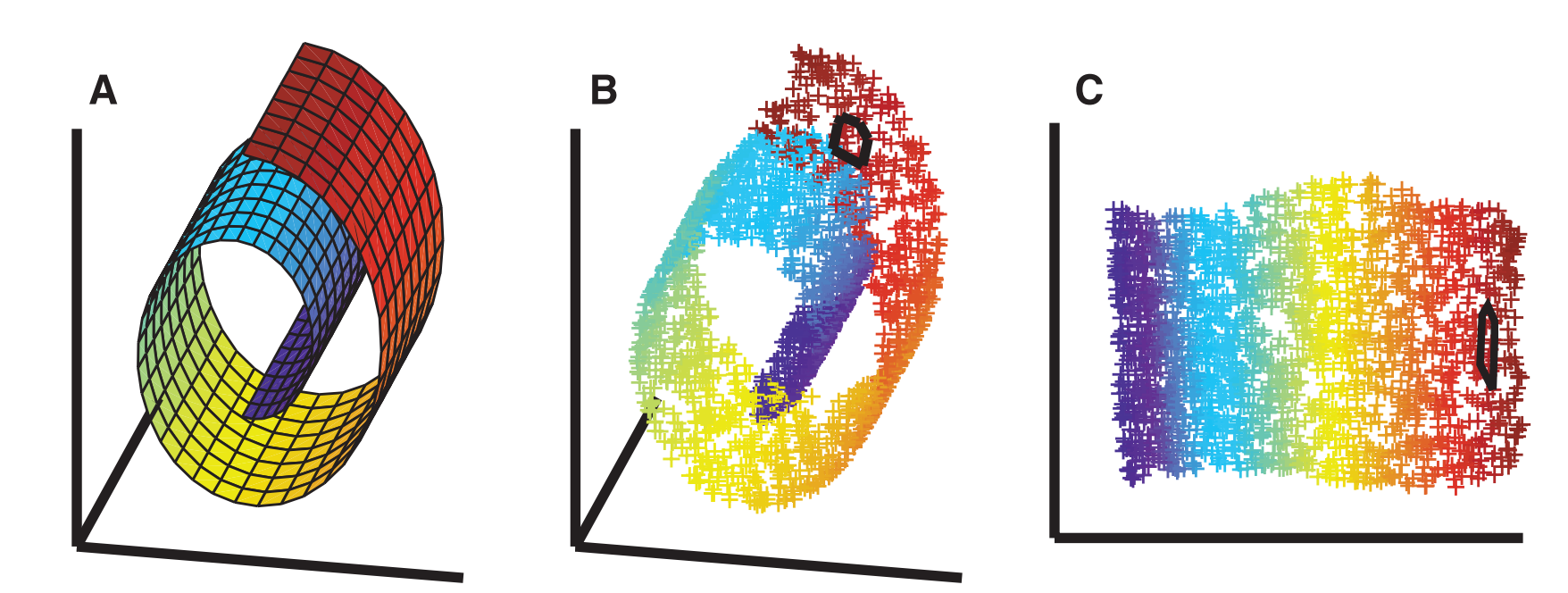
위와 같이 둘둘 말린 형태의 데이터를 swiss-roll data 라 합니다. ISOMAP 은 manifold 에서의 이웃 간의 정보를 보존하는 2 차원 평면을 학습할 수 있습니다.

Scikit-learn 은 ISOMAP 을 제공합니다. 이 역시 원 공간에서의 nearest neighbors 의 개수를 설정할 수 있습니다.

from sklearn.manifold import Isomap

y = Isomap(n_components=2, n_neighbors=5).fit_transform(x) # x: numpy.ndarray

ISOMAP 은 고차원 공간의 시각화 보다는 manifold 공간의 시각화를 위하여 이용되는 알고리즘입니다. 그리고 nearest neighbors 의 개수에 매우 민감합니다. 또한 graph 로 연결되지 않는 점들 간의 거리는 무한대가 되며, 연결되지 않는 부분 공간들은 임베딩 결과 서로 겹칠 수도 있습니다. LLE 의 실험에서 이용하였던 데이터에 대하여 ISOMAP 역시 nearest neighbors 의 개수를 조절하며 임베딩 공간을 학습합니다.

from sklearn.manifold import Isomap

plots = []
for n_neighbors in [2, 3, 5, 10]:
    z = Isomap(
        n_components=2,
        n_neighbors=n_neighbors
    ).fit_transform(x)
    title = 'ISOMAP with n_neighbors = {}'.format(n_neighbors)
    plots.append(draw_figure(z, y, title, show_figure=False))

gp = gridplot([[plots[0], plots[1]], [plots[2], plots[3]]])
show(gp)

Nearest neighbors 가 2 일 때에는 분리된 공간인 주황색이 scatter plot 의 중심에 다른 점들과 겹쳐서 그려졌습니다. Nearest neighbors = 2 일 때에는 왼쪽 오른쪽 손을 잡고 연결된 형태이기 때문에 한 줄로 늘어선 형태의 임베딩 공간이 학습되었습니다. Nearest neighbors = 3 일 때에는 데이터에서 빨간색과 에머럴드 색간에 nearest neighbors 로 연결된 한 점이 존재하였기 때문에 이들이 이어져 임베딩이 됩니다. 그리고 이들과 연결되지 않은 주황색 점들은 가운데에 떨어져 위치합니다. 이후에도 neighbors = 5, 10 일 때 역시 주황색은 독립적으로 떨어지며, 빨간색과 에머럴드 색은 경계를 맞대고 학습됨을 볼 수 있습니다. 이 역시 원 공간의 정보를 보존하지는 못합니다.

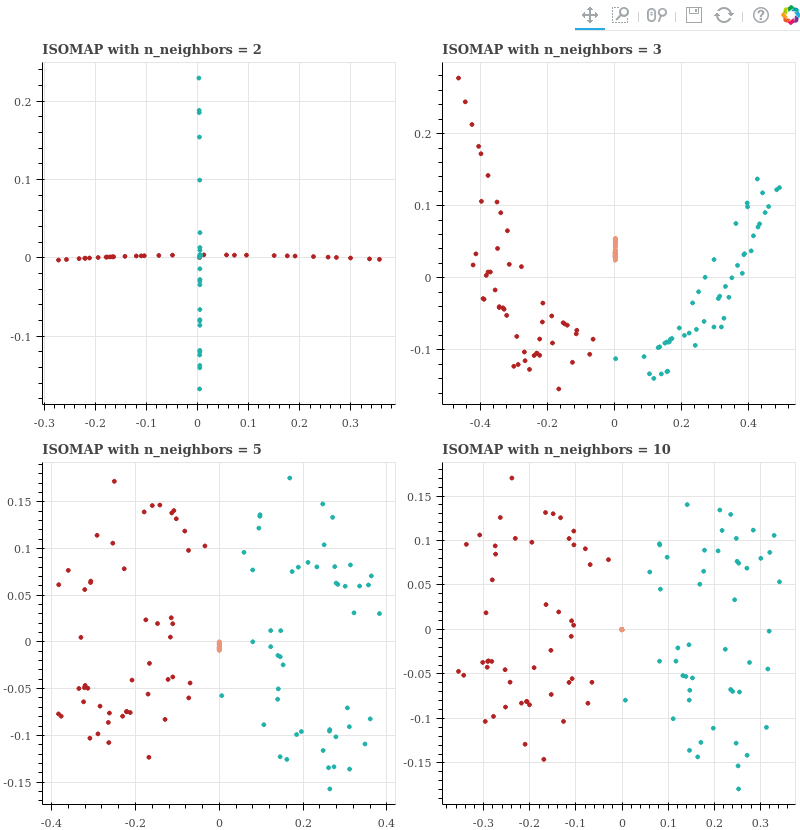
t-Stochastic Neighbor Embedding (t-SNE)

t-Stochastic Neighbor Embedding (t-SNE) 은 고차원의 원 공간 $x$ 에서 가까이 위치한 점들이 저차원의 임베딩 공간 $y$ 에서도 가까이 위치할 수 있도록 locality 를 보존하며 차원을 축소합니다. 고차원 공간에서 가까이에 위치한 점들의 정보는 확률로 정의됩니다. 이는 stochastic probability 형식입니다. 이를 정의하기 위하여 기준점 $x_i$ 에서 다른 모든 점들과의 Euclidean distance 인 $\vert x_i - x_j \vert$ 를 계산하고 이 거리를 기반으로 $x_i$ 에서 $x_j$ 까지 얼마나 가까운지 확률로 나타냅니다. $exp(- \vert x_i - x_j \vert^2 / 2 \sigma_i^2)$ 는 모든 값이 non-negative 이며, 두 점 간의 거리가 가까울 수록 큰 값이 됩니다. 모든 점들과의 $exp(- \vert x_i - x_k \vert^2 / 2 \sigma_i^2)$ 의 거리의 합으로 각각을 나눠주면 확률 형식이 됩니다. $\sigma_i$ 는 모든 점 $x_i$ 마다 다르게 정의됩니다.

$p_{j \vert i} = \frac{exp(- \vert x_i - x_j \vert^2 / 2 \sigma_i^2)}{\sum_{k \neq i} exp(- \vert x_i - x_k \vert^2 / 2 \sigma_i^2)}$

이 때 locality 만을 보존하는 것이 아니라, 데이터 공간의 local structure 와 global structure 를 동시에 고려합니다. 그리고 local area 의 경계는 perplxity 에 의하여 조절됩니다. 모든 점이 0 이상의 $p_{j \vert i}$ 의 값을 지니기 때문에 global structure 정보를 만들 수 있습니다.

각 점마다 $\sigma_i$ 가 다르기 때문에 $p_{j \vert i}$ 와 $p_{i \vert j}$ 가 다를 수 있습니다. 점 간의 유사도를 대칭적으로 만들기 위하여 두 확률 값의 평균으로 두 점간의 유사도를 정의합니다. 그리고 데이터 전체에 $n$ 개의 점이 존재하니 다시 한 번 $n$ 개의 점으로 나눠주면 모든 점들 간의 유사도의 합이 1 이 되도록 만듭니다. $p_{ij}$ 는 $n$ 개의 점들 간에 $x_i, x_j$ 가 상대적으로 얼마나 가까운지를 나타내는 값이 됩니다.

$p_{ij} = \frac{p_{i \vert j} + p_{j \vert i}}{2n}$

이번에는 임베딩 공간에서의 두 점 간의 유사도 $q_{ij}$ 를 정의합니다. 두 점 간의 거리 $\vert y_i - y_j \vert^2$ 가 작을수록 유사도가 클 수 있도록 임베딩 공간의 거리에 1 을 더한 뒤 역수를 취합니다. 그리고 모든 점들 간의 $\left( 1 + \vert y_k - y_l \vert^2 \right)^{-1}$ 의 합으로 나눠줌으로써 전체의 합이 1 이 되도록 합니다.

$q_{ij} = \frac{ \left( 1 + \vert y_i - y_j \vert^2 \right)^{-1} }{\sum_{k \neq l} \left( 1 + \vert y_k - y_l \vert^2 \right)^{-1} }$

t-SNE 는 $p_{ij}$ 에 가장 가깝도록 $q_{ij}$ 를 학습합니다. 학습에는 gradient descent 를 이용합니다. 현재 공간 $y$ 에서의 좌표값으로부터 만든 $q$ 가 $p$ 와 다르다면 더 비슷할 수 있는 방향으로 $y$ 의 점들을 이동합니다. 그 이동정도는 아래와 같습니다. 이는 원 공간에서 $x_i$ 가 $x_j$ 에 가까운데, $y_i$ 와 $y_j$ 가 멀리 떨어져 있다면 $y_i$ 를 $y_j$ 방향으로 밀어 이 둘을 가까이 위치하게 만듭니다. 모든 점에 대하여 이 과정을 반복하면 원 공간에서의 점들 간의 유사도를 보존하는 임베딩 공간 벡터 $y$ 를 학습할 수 있습니다.

$\frac{\delta C}{\delta y_i} = \sum_j (p_{ij} - q_{ij})(y_i - y_j)\frac{1}{1 + \vert y_i - y_j \vert^2}$

이를 이용하여 0 부터 9 까지의 숫자 손글씨로 이뤄진 (28, 28) 크기의 MNIST 데이터를 임베딩하면 아래 그림과 같습니다. 같은 숫자는 같은 색의 점입니다. 784 차원의 고차원 이미지 벡터가 2 차원으로 임베딩되어도 같은 종류의 숫자끼리는 거의 한 군집에 모여 있습니다.

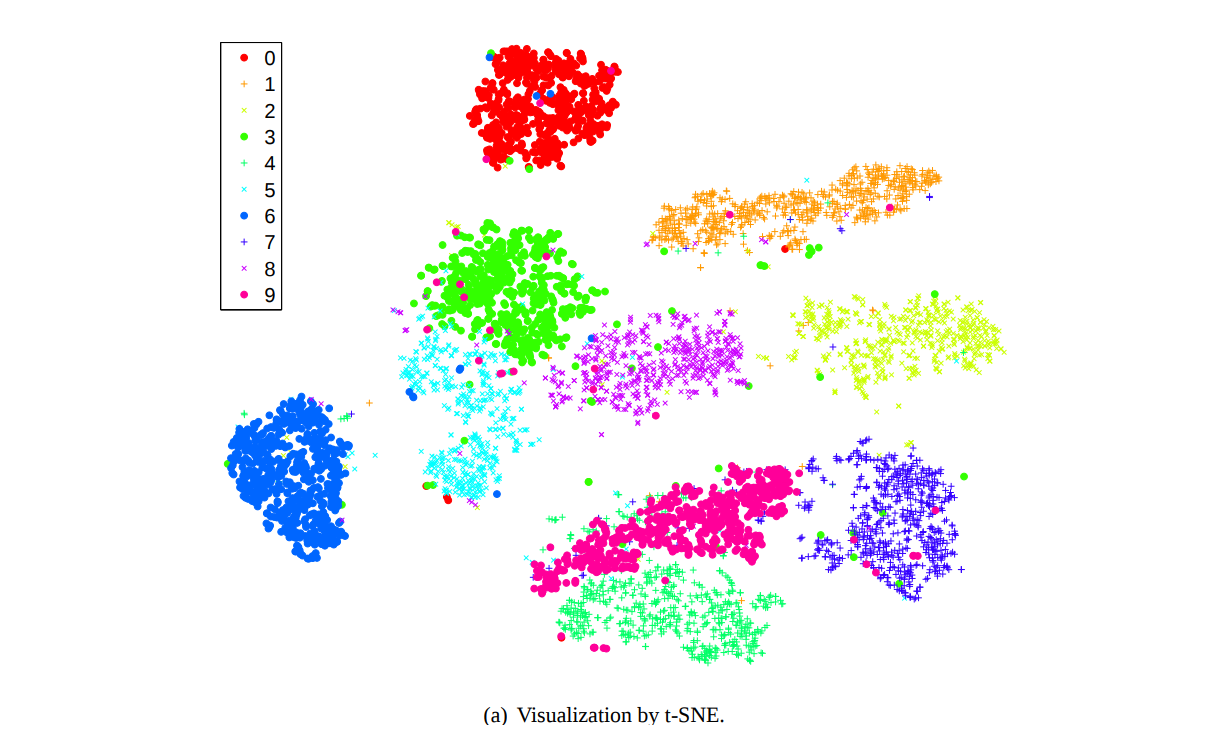
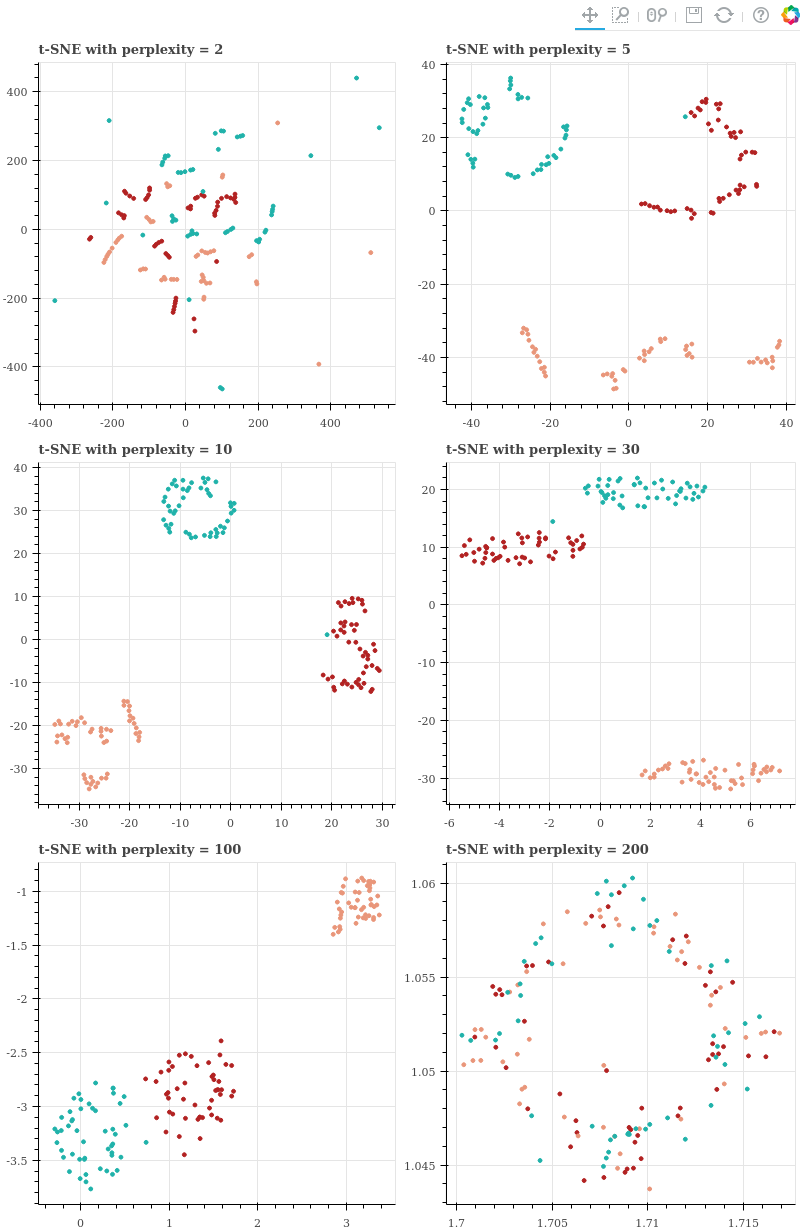
앞서 LLE 와 ISOMAP 은 인공으로 만든 (고작) 150 개의 데이터의 구조도 제대로 보존하지 못한 임베딩 공간을 학습하였습니다. 사실 비판할 것이 아니라, LLE 와 ISOMAP 은 시각화에 필요한 정보를 보존하지 않은 것 뿐입니다. 그들은 manifold 와 같이 꼬여있는 공간을 시각화 하기 위한 임베딩 방법이기 때문입니다. t-SNE 를 이용하여 위 데이터의 2 차원 임베딩 공간을 학습합니다. t-SNE 의 locality 를 설정하는 perplexity 값을 바꿔가며 실험을 수행합니다. 지나치게 작은 perplexity 인 2 부터 지나치게 큰 값인 200 까지 설정하였습니다.

from sklearn.manifold import TSNE

plots = []
for perplexity in [2, 5, 10, 30, 100, 200]:
    z = TSNE(
        n_components=2,
        perplexity=perplexity
    ).fit_transform(x)
    title = 't-SNE with perplexity = {}'.format(perplexity)
    plots.append(draw_figure(z, y, title, show_figure=False))

gp = gridplot([[plots[0], plots[1]], [plots[2], plots[3]], [plots[4], plots[5]]])
show(gp)

그 결과 perplexity 가 지나치게 작은 2 일 때에는 LLE 처럼 지나치게 좁은 locality 만이 반영되어 왜곡된 공간이 학습되었습니다. Perplexity = 5 일 때에는 각 클래스별로 조금씩 뭉쳐져 있는 점들 끼리 그룹을 지었습니다. 하지만 그룹 간의 거리도 어느 정도 보존되었습니다. Perplexity 가 10 ~ 100 일 때에는 각 클래스 간 간격이 어느 정도 보존되었습을 알 수 있습니다. 하지만 perplexity = 200 처럼 매우 큰 값을 이용하면 점들 사이에 가깝고 먼 정보가 사라져 원 공간의 거리 정보가 보존되지 않습니다. 하지만 t-SNE 는 perplexity 에 크게 민감하게 반응하지 않고 안정적으로 원 공간의 구조를 보존함을 알 수 있습니다. 그리고 이는 고차원 공간의 임베딩에서도 동일합니다.

이전 포스트에서 $p_{ij}$ 와 $q_{ij}$ 가 위와 같은 분포를 따르는 이유와 perplexity 의 의미 및 역할에 대하여 이야기하였습니다. 이에 대한 내용은 이전의 t-SNE 포스트를 참고하시기 바랍니다.

Embedding space of term - document matrix

LLE 의 논문에서 소개된 것처럼 term - document matrix 를 임베딩하면 topically similar words 를 비슷한 임베딩 벡터를 지니도록 학습할 수 있습니다. 2016-10-20 일 뉴스의 명사를 이용하여 실험을 합니다. Tokenization 은 모두 수행한 30,091 건의 뉴스로, 9,774 개의 단어로 구성되어 있습니다. 네 알고리즘의 계산 시간을 알아보기 위하여 time package 를 이용하여 시간을 측정합니다.

# transpose & sparse to dense
x = x.transpose()
x_dense = x.todense()

# normalize
from sklearn.preprocessing import normalize
x_dense = normalize(x_dense, axis=1, norm='l2')

names = 'tsne mds lle isomap'.split()
methods = [
    TSNE(n_components=2),
    MDS(n_components=2),
    LocallyLinearEmbedding(n_components=2),
    Isomap(n_components=2)
]

# learning
import time
for name, method in zip(names, methods):
    t = time.time()
    y = method.fit_transform(x_dense)
    t = time.time() - t
    print('{}, {:.3f} sec'.format(name, t))

고작 9.774 개의 단어의 임베딩을 학습하는데 모두들 한 시간이 넘는 계산을 하였습니다. 큰 데이터의 시각화를 위한 임베딩에는 쓰기가 어렵습니다. 메모리 사용량은 제대로 확인하지 못했지만, 약 7 Gb 이상을 계속 이용하였습니다. (다시 학습하고 싶지 않네요)

method	computation time [sec]
t-SNE	4229.715
MDS	3734.525
LLE	4089.274
ISOMAP	4009.104

학습한 임베딩 공간을 Bokeh 를 이용하여 그려 봅니다. 아래의 네 그림은 Bokeh 를 이용하여 그린 HTML 의 스냅샷입니다. HTML 파일의 크기가 커서 이는 링크로 공유합니다. HTML 파일을 브라우저로 여시면 toolbar 를 이용하여 공간을 drag zoom-in/out 할 수 있으며, 점 위에 마우스 커서를 올려두면 해당 좌표와 단어가 표시됩니다.

from bokeh.models import ColumnDataSource, Div
from bokeh.plotting import figure, output_notebook, show, output_file

output_notebook()

def draw_figure(coordinates, index2word, title):
    TOOLTIPS=[
        ("word", "@word"),
        ("x", "@x"),
        ("y", "@y")
    ]

    source = ColumnDataSource(data=dict(word=[], x=[], y=[]))
    source.data = dict(
        word=index2word,
        x=coordinates[:,0].reshape(-1).tolist(),
        y=coordinates[:,1].reshape(-1).tolist()
    )

    p = figure(plot_height=600, plot_width=600, title=title, tooltips=TOOLTIPS)
    p.circle(
        x="x",
        y="y",
        source=source,
        size=5,
        line_color='firebrick',
        fill_color='firebrick',
        fill_alpha=0.3
    )
    return p

import pickle
with open('/mnt/lovit/works/fastcampus_text_ml/2nd/data/corpus_10days/models/params_keywords', 'rb') as f:
    params = pickle.load(f)
    index2word = params['index2word']

output_file('embedding_for_vis_termdoc.html')
for name in 'tsne mds lle isomap'.split():
    with open('./embedding_for_vis_2016-10-20-{}.pkl'.format(name), 'rb') as f:
        y = pickle.load(f)    
    p = draw_figure(y, index2word, name + ' (term=9,774, doc=30,091, 2016-10-20 news)')
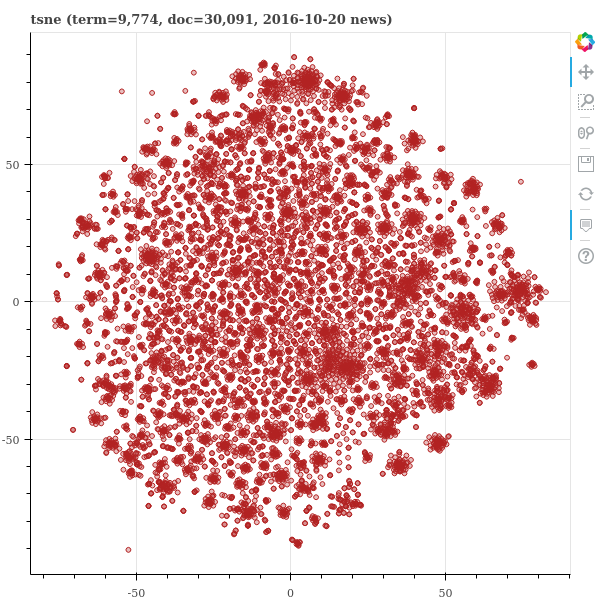
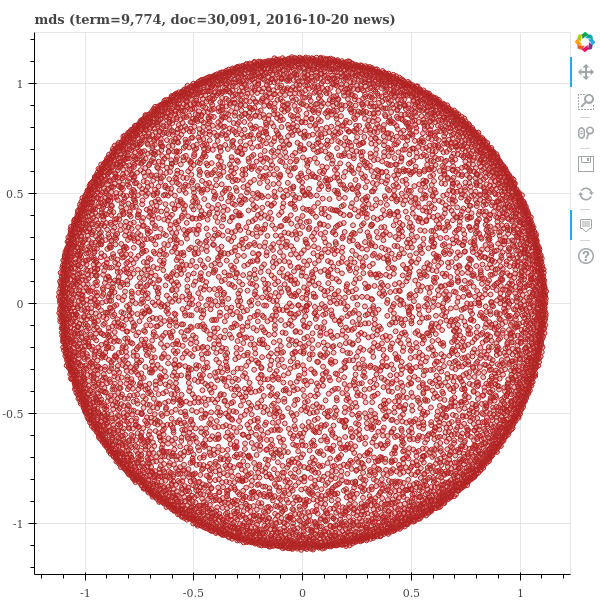
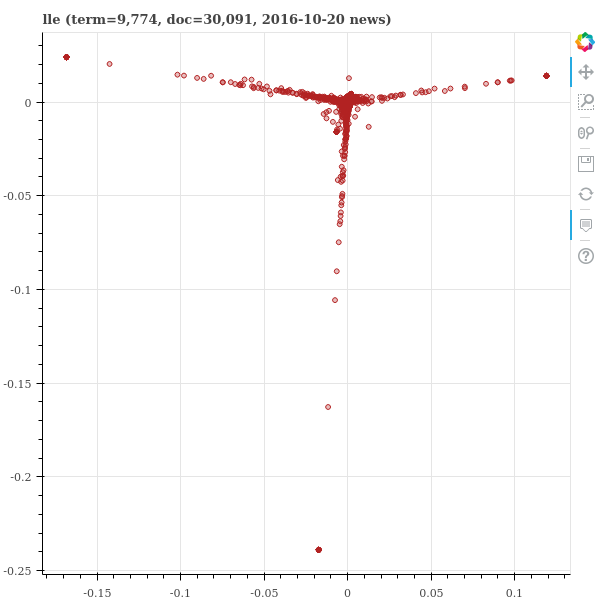
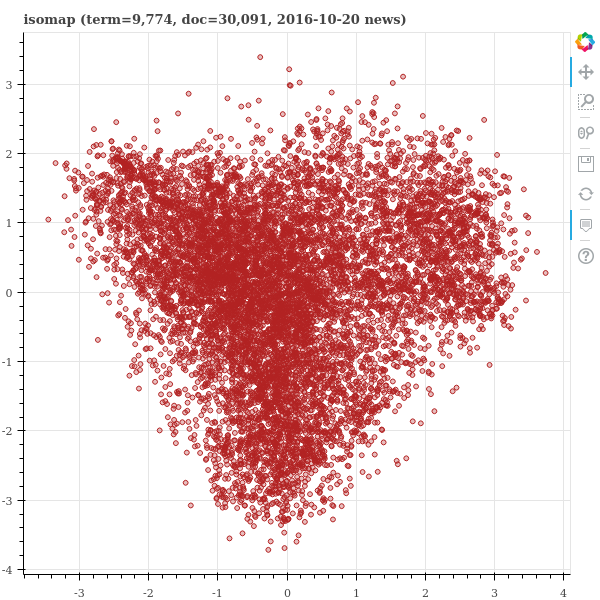
    show(p)

아래 그림에서 t-SNE 는 부분적으로 방사형을 띄고, 전체적으로는 원형을 띕니다. 이는 Barnes-hut tree 를 이용하는 t-SNE 의 전형적인 임베딩 공간 패턴입니다. 그리고 대체로 납득될만한 공간이 학습되었습니다. 하지만 그 아래 MDS 는 가득찬 원을 그립니다. 그리고 왠만한 고차원 공간에서는 이러한 모습을 보입니다. 이전의 k-means 포스트에서 언급하였듯이 고차원 공간에서는 대부분의 pairwise distances 가 비슷한 값을 지닙니다. 그리고 MDS 는 대부분의 정보가 무의미한 pairwise distances 정보를 보존하려 노력하다보니 이러한 모양으로 임베딩 공간을 학습합니다. LLE 는 예시 데이터에서와 같이 직선형으로 늘어선 임베딩 공간을 학습합니다. Global structure 가 반영되지 않은 임베딩 공간을 학습하였습니다. ISOMAP 은 이번 예시에서는 어느 정도 괜찮은 그림이 그려졌습니다만, 조금 더 날카로운 형태의 모양을 띄는 경우가 많습니다. 그리고 중심부로 들어간 모양의 공간이 학습되는 경우가 많습니다.

Reference

Kruskal, J. B. (1964). Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika, 29(1), 1-27.
Roweis, S. T., & Saul, L. K. (2000). Nonlinear dimensionality reduction by locally linear embedding. Science, 290
Tenenbaum, J. B., De Silva, V., & Langford, J. C. (2000). A global geometric framework for nonlinear dimensionality reduction. Science,
Van der Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(2579-2605), 85.