t-Stochastic Nearest Neighbor (t-SNE) 는 vector visualization 을 위하여 자주 이용되는 알고리즘입니다. t-SNE 는 고차원의 벡터로 표현되는 데이터 간의 neighbor structure 를 보존하는 2 차원의 embedding vector 를 학습함으로써, 고차원의 데이터를 2 차원의 지도로 표현합니다. t-SNE 는 벡터 시각화를 위한 다른 알고리즘들보다 안정적인 임베딩 학습 결과를 보여줍니다. 이는 t-SNE 가 데이터 간 거리를 stochastic probability 로 변환하여 임베딩에 이용하기 때문입니다. 그리고 이 stochastic probability 는 perplexiy 에 의하여 조절됩니다. 이번 포스트에서는 t-SNE 가 어떻게 안정적인 임베딩 학습 결과를 보일 수 있는지에 대한 원리를 살펴보고, perplexity 의 역할에 대해서도 알아봅니다.
Dimension reduction for visualization
고차원의 벡터를 이해하기 위하여 시각화 방법들이 이용됩니다. 대표적인 방법으로 t-SNE 라 불리는 t-Stochastic Neighbor Embedding 이 있습니다. t-SNE 는 고차원 공간에서 유사한 두 벡터가 2 차원 공간에서도 유사하도록, 원 공간에서의 점들 간 유사도를 보존하면서 차원을 축소합니다. 우리가 이해할 수 있는 공간은 2 차원 모니터 (지도) 혹은 3 차원의 공간이기 때문입니다.
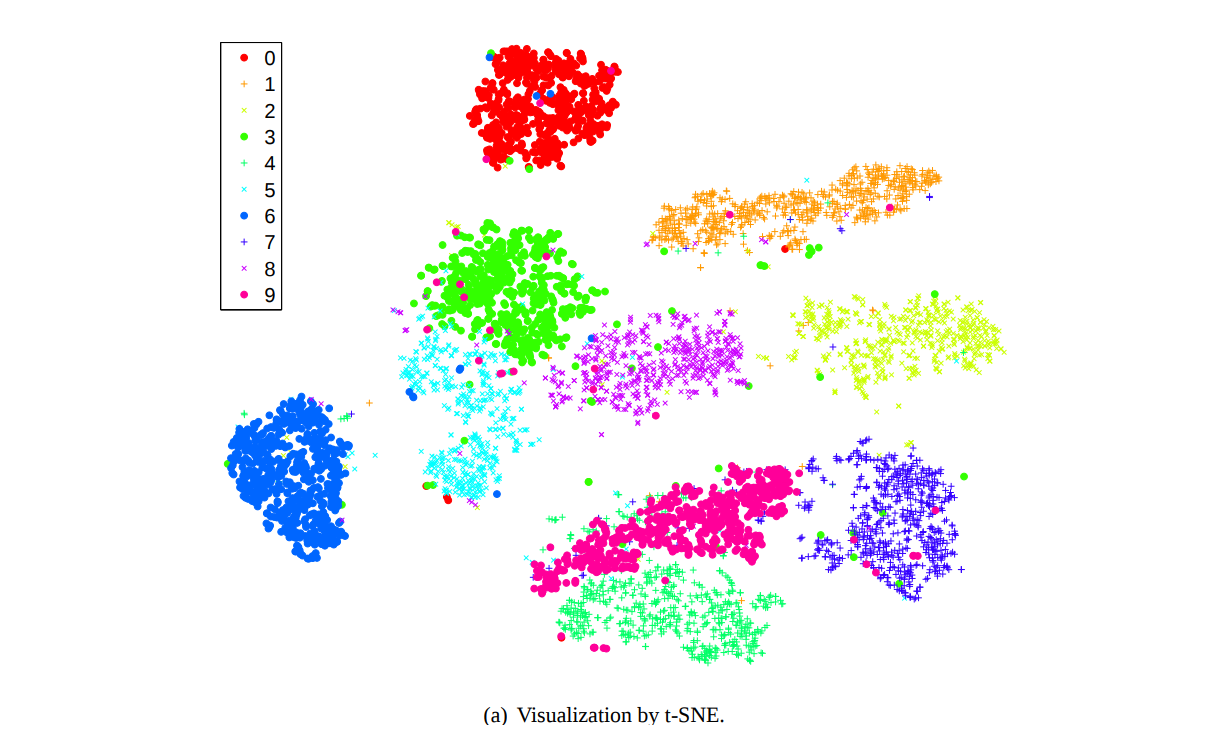
위 그림은 t-SNE 가 제안되었던 Maaten (2008) 에서 10 개의 숫자 손글씨인 MNIST 데이터를 2 차원으로 압축하여 시각화한 그림입니다. 같은 색은 같은 숫자를 의미합니다. MNIST 는 (28, 28) 크기의 784 차원 데이터입니다. 우리가 784 차원을 상상할 수는 없지만, 이를 2 차원으로 압축하면 어떤 이미지들이 유사한지 시각적으로 이해할 수 있습니다.
최근에 깊게 연구되고 있는 딥러닝 모델들은 학습된 지식의 형태를 distributed representation 으로 저장합니다. 해석 불가능한 고차원의 dense vector 로 저장한다는 의미입니다. 대체로 이 벡터의 크기는 매우 큽니다. Sentence classification 이나 image classification 을 위한 Convolutional Neural Network (CNN) 모델이 softmax layer 에 내보내는 마지막 output 은 sentence 에 대한 distributed representation 입니다. Recurrent Neural Network (RNN) 의 hidden vector 들의 차원도 고차원입니다. 이들을 해석할 수는 없지만, 비슷한 input 이 비슷한 distributed representation 을 얻는지 확인하기 위하여 고차원 벡터의 시각화는 필요합니다.
물론 deep learning models 은 그 자체로 데이터 시각화를 할 수도 있습니다. 아래 그림은 Hinton 교수님의 2006 년도 논문에서 제안된 autoencoder 입니다. Restricted Boltzmann machines (RBM) 을 stacking 하여 모델을 구성하였습니다.
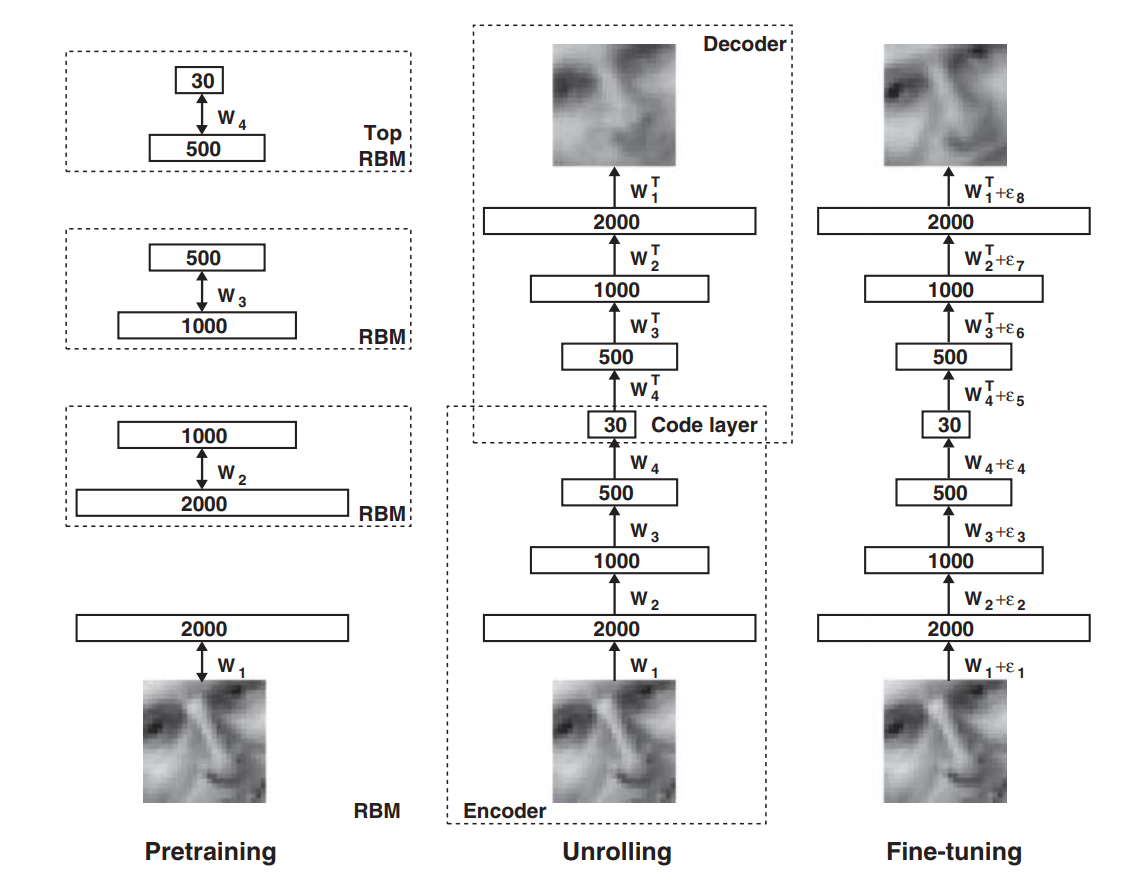
약 2 만 개의 단어로 표현되는 20 News group 문서에 대해 문서 간 유사도 정보를 보존하는 2 차원 좌표를 학습하기 위하여 가장 깊은 encoder layer 의 차원을 2 까지 줄였습니다. 그리고 그 2 차원 벡터를 x, y 축으로 plotting 하면 아래와 같은 그림을 얻을 수 있습니다.
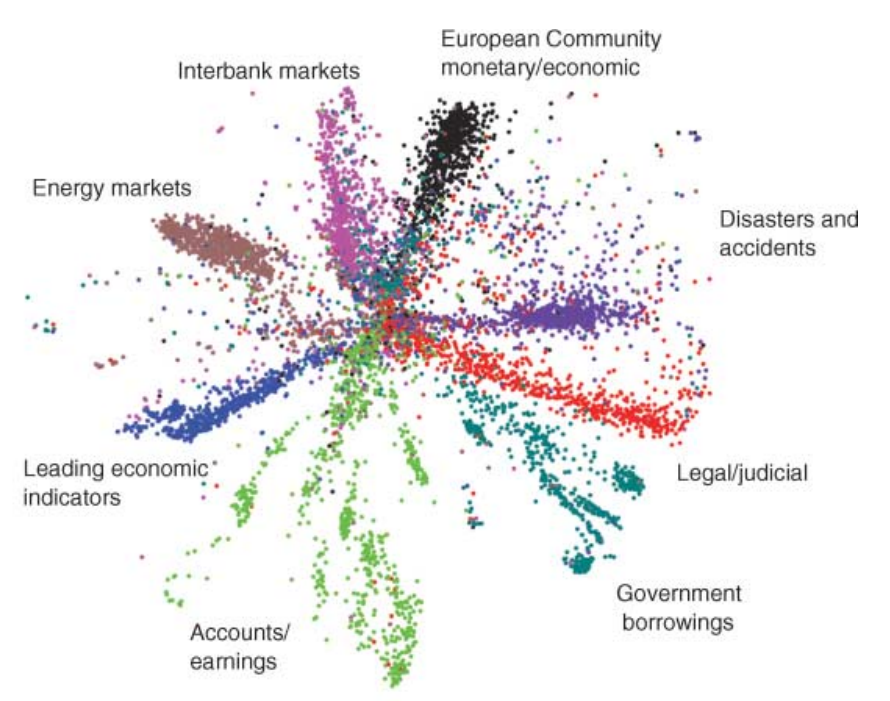
그러나 위 그림처럼 정보를 지나치게 압축하면 autoencoder 의 복원력에 문제가 생길 수 있습니다. 복잡한 문제를 푸는 deep learning models 은 최소한의 공간이 확보되어야 하고, 그 과정에서 자연스레 고차원의 벡터가 발생합니다. 결국 이들을 해석하려면 다시 한 번 dimension reduction 을 하여야 합니다. 그리고 이 때 PCA 와 t-SNE 가 자주 이용됩니다. 물론 다른 알고리즘들도 이용할 수는 있지만, PCA 와 t-SNE 가 robust 한 결과를 학습하는 경우가 많습니다. 우리는 이번 포스트에서 t-SNE 의 학습 원리에 대해 살펴봅니다.
t-Stochastic Neighbor Embedding (t-SNE)
Motivation
벡터 시각화를 위한 차원 축소, 임베딩 알고리즘들은 이전에도 제안되었습니다. 1960 년대에 제안되었던 Multi-Dimensional Scaling (MDS) 부터 2000 년에 제안된 ISOMAP 와 Locally Linear Embedding (LLE) 모두 고차원의 정보를 저차원으로 축소하려는 알고리즘입니다. 그 목적은 아니지만, Pincipal Components Analysis (PCA) 역시 고차원에서의 거리 정보를 보존하여 저차원으로 차원을 변환하는 기능을 가지고 있기도 합니다.
이렇게 다양한 알고리즘들이 제안된 이유는 각 알고리즘마다 보존하려는 정보가 다르기 때문입니다. 한 공간에서 다른 공간으로 변환을 하기 때문에 어떤 정보는 부각되고, 어떤 정보는 줄어듭니다. 특히 시각화를 위하여 차원을 매우 크게 줄인다면 넓은 공간에 존재하였던 정보 중 일부는 손실 될 수 있습니다. 여러 알고리즘들은 각자가 선택적으로 보존하고 싶은 정보가 다릅니다. MDS 는 멀리 떨어진 점들이 여전히 멀리 떨어져 있기를 원했습니다. 가까운 점들이 조금 멀어지는 것은 신경쓰지 않습니다. ISOMAP 은 차원 축소라기 보다는 뭬비우스의 띠처럼 꼬여있는 공간을 평면으로 풀기를 원했습니다. 정확히는 nearest neighbor graph 에서 정의되는 거리를 보존하는 지도를 그리고 싶어합니다. LLE 는 고차원에서 nearest neighbors 이었던 k 개의 점들은 저차원에서도 nearest neighbors 가 되기를 원합니다. 그리고 k 번으로 가까운 점이 아니면 어디에 있던지 상관하지 않습니다. 이처럼 큰 공간에서 작은 공간으로 이동하는 도중에 특별히 보존하고 싶은 정보들이 다르기 때문에 여러 방법들이 제안되었습니다. 이들에 대해서는 다른 포스트에서 자세히 알아보고, 이번에는 t-SNE 이야기만 하겠습니다.
위 방법들 중 t-SNE 와 가장 가까운 방법은 LLE 입니다. t-SNE 도 원 공간에서 가까운 점들은 차원이 축소된 공간에서도 가깝기를 바랍니다. 그런데, LLE 의 단점 중 하나는 k 개의 가장 가까운 점들은 신경쓰지만 그 외의 점들은 전혀 신경쓰지 않는다는 점입니다. 사실 전혀 신경쓰지 않아도 전체의 구조가 (자연스레, 우연히) 보존될 수 있지만, 반드시 보존된다는 보장은 하지 못합니다. 이를 해결하기 위해서는 원 공간에서 가까운 점들도 고려하지만, 좀 더 멀리 있는 점들의 위치도 신경써야 합니다. 이 구절도 개인적으로 좋아하는 구절입니다. t-SNE 의 논문에 나온 구절을 인용하였습니다.
또한 k 는 사용자가 정의하는 parameter 입니다. 데이터 마다 이 값을 다르게 선택해야 합니다. 그런데 사용자가 학습 parameter 를 크게 신경쓰지 않는다면 어느 데이터에 적용하여도 안정적인 결과를 보여줄 것입니다. t-SNE 도 perplexity 라는 parameter 를 설정해야 하지만, 이 값에 아주 예민하게 작동하지는 않습니다. 대체로 잘 작동하는 값이 있습니다. 그리고 perplexity 를 이용하여 데이터 간 거리를 정의하는 방식 자체가 안정성을 더해줍니다. t-SNE 가 다른 알고리즘보다 널리 쓰이게된 이유는 이러한 robustness 때문이라 생각합니다. 다음 장에서 t-SNE 가 어떻게 안정적인 차원 축소 결과를 학습하는지 알아봅니다.
How to embed high dimensional vectors to low dimensional space
고차원의 원 공간에서 저차원의 임베딩 공간으로 데이터의 공간을 변환하기 위해서 t-SNE 는 원 공간에서의 데이터 간 유사도 와 임베딩 공간에서의 데이터 간 유사도 를 정의합니다.
를 정의하기 위해 먼저 점 에서 로의 유사도인 를 정의해야 합니다. 이 유사도는 확률 형식입니다. 이를 정의하기 위해서는 먼저 기준점 에서 다른 모든 점들과의 Euclidean distance 인 를 계산합니다. 그리고 이 거리를 기반으로 에서 까지 얼마나 가까운지 확률로 나타냅니다. 이를 위해서 먼저 와 의 거리를 로 나누고 negative exponential 을 취합니다. 는 모든 값이 non-negative 이며, 두 점 간의 거리가 가까울 수록 큰 값이 됩니다. 모든 점들과의 의 거리의 합으로 각각을 나눠주면 확률 형식이 됩니다. 는 모든 점 마다 다르게 정의됩니다. 이 부분이 t-SNE 가 안정적인 학습 결과를 가지게 된 결정적인 부분입니다. 바로 뒤에서 자세히 설명하겠습니다.
알고리즘에 stochastic 이라는 이름이 붙은 이유는 가 마치 stochastic modeling 역할을 하기 때문입니다. Stochastic modeling 은 매 시점마다 확률 분포를 따라 어떤 점이 다른 점으로 이동하는 모델을 의미합니다. 어떤 사람 한 명이 현재 에 위치할 때, 다음 시점에 다른 점 로 이동할 확률을 로 정의하는 것입니다. 즉 가까울수록 높은 확률로 점들을 이동하는 모델입니다.
잠깐 이름의 유래를 살펴보았습니다. 다시 알고리즘으로 돌아옵니다. 앞서 점 에서 로의 이동 확률을 정의하였습니다. 이 값을 이용하여 두 점 와 의 유사도를 정의합니다. 위 정의에서는 와 가 다를 수 있습니다. 왜냐면 각 점마다 가 다르기 때문입니다. 점 간의 유사도를 대칭적으로 만들기 위하여 두 확률 값의 평균으로 두 점간의 유사도를 정의합니다. 그리고 데이터 전체에 개의 점이 존재하니 다시 한 번 개의 점으로 나눠주면 모든 점들 간의 유사도의 합이 1 이 되도록 만들 수 있습니다. 는 개의 점들 간에 가 상대적으로 얼마나 가까운지를 나타내는 값이 됩니다. 그리고 어떤 점들 간의 유사도도 을 넘을 수 없습니다. 가 1 보다 작은 확률이기 때문입니다.
물론 를 아래와 같이 정의할 수도 있습니다. 모든 에 대하여 동일한 를 이용하는 것입니다. 그런데 아래와 같은 정의를 이용하면 outliers 에 크게 휘둘릴 수 있습니다. 만약 가 다른 점들과 동떨어져 있는 값이라면 다른 점들과의 거리 가 매우 크게 됩니다. 이는 를 큰 값으로 만들기 때문에 가까운 두 점 간의 거리로부터 유도되는 분자, 를 매우 작게 만듭니다. 모든 점마다 를 다르게 정의한 이유는 각 점들의 사정을 고려하여 를 완만하게 만들고 싶기 때문입니다.
지금까지 원 공간에서의 두 점 간의 유사도 를 정의하였습니다. 이번에는 임베딩 공간에서의 두 점 간의 유사도 를 정의합니다. 이 값도 이 되도록 정의하였습니다. 두 점 간의 거리 가 작을수록 큰 값을 지니도록 이 값의 역수를 취하여 을 유사도로 이용할 수도 있습니다. 그런데 0 에 가까운 값의 역수는 무한대에 가깝습니다. 그렇기 때문에 처럼 1 을 더하여 역수를 취하면 안정적으로 역수를 구할 수 있습니다. 그리고 이 값은 확률 분포인 t-distribution 입니다. 본래 SNE 라는 알고리즘이 있었습니다. 점들 간의 유사도를 stochastic probability 로 정의하는 이 연구에서 임베딩 공간의 점들 간 유사도 분포를 t-distribution 으로 바꿈으로써 더 안정적인 학습 결과를 얻어낸 알고리즘이 t-SNE 입니다.
이번에도 모든 점들 간의 의 합으로 나눠줌으로써 전체의 합이 1 이 되도록 하였습니다.
그리고 t-SNE 는 에 가장 가깝도록 를 학습합니다. 정확히는 를 정의하는 를 학습합니다. 이는 정답지 를 보면서 의 위치를 이동하는 것과 같습니다.
학습에는 gradient descent 를 이용합니다. 현재 공간 에서의 좌표값으로부터 만든 가 와 다르다면 더 비슷할 수 있는 방향으로 의 점들을 이동합니다. 그 이동정도는 아래와 같습니다.
만약 와 가 비슷하면 이동하지 않습니다. 그러나 원 공간에서 가 에 가까웠다면 를 방향으로 이동시킵니다. 한 점 에 대하여 자신이 이동해야 할 공간으로 이동하고, 다음 점도 자신이 있어야할 자리를 찾아 조금씩 이동합니다. 모든 점들이 순차적으로 자신이 가야할 곳으로 이동하는 것을 반복하면 원 공간에서 가까운 점들이 임베딩 공간에서도 가깝게 됩니다.
Package: sklearn
t-SNE 는 논문의 저자인 Maaten 을 비롯한 많은 사람들이 구현체를 공유하였습니다. scikit-learn 에도 t-SNE 구현체가 제공됩니다. 제 기억에 0.19.0 에서 0.19.1 로 버전업이 될 때 distance 관련한 몇 가지가 업그레이드 되었고, 이후로 더 안정적인 학습 결과가 나왔습니다. 사용하실 때 반드시 0.19.1+ 로 이용하시기 바랍니다.
t-SNE 도 설정할 수 있는 parameters 가 많지만, 특별히 신경써야 할 parameters 는 아래와 같습니다. 이들의 역할에 대하여 하나씩 알아보도록 하겠습니다.
from sklearn.manifold import TSNE
TSNE(n_components=2, perplexity=30.0, early_exaggeration=12.0,
learning_rate=200.0, n_iter=1000, n_iter_without_progress=300,
min_grad_norm=1e-07, metric='euclidean', init='random', verbose=0,
random_state=None, method='barnes_hut', angle=0.5)
| parameter | note |
|---|---|
| n_components | 임베딩 공간의 차원 |
| perplexity | 의 기준, 학습에 영향을 주는 점들의 개수를 조절 |
| metric | 원 공간에서의 두 점간의 거리 척도 |
| method | 원 공간 데이터의 인덱싱 방식 |
t-SNE 의 사용 방법은 간단합니다. 아래처럼 TSNE 를 만든 뒤 fit_transform 만 실행하면 됩니다. 이 때 n_components 는 임베딩 공간의 차원 크기 입니다. 시각화를 위하여 2 로 설정합니다.
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2)
y = tsne.fit_transform(x)단, x 는 scipy.sparse 를 입력할 수 없습니다. numpy.ndarray 형식의 dense matrix 만 입력가능합니다. 이는 scikit-learn 의 t-SNE 가 method=’barnes_hut’ 을 이용하고 있기 때문인데, 이 방법이 sparse matrix 를 지원하지 않습니다.
다른 parameters 에 대해서도 알아봅니다.
Barnes hut t-SNE
그런데 위 식의 정의를 살펴보면 와 를 계산하기 위해서는 번의 거리 계산을 수행해야 합니다. 의 비용이 드는 알고리즘은 왠만하면 지양하는 것이 좋습니다. 계산 시간이 오래 걸릴 뿐더러 메모리 비용부터 어마무시 합니다. 실제로 위 공식의 t-SNE 는 1 만개 points 의 임베딩을 위해서 몇 시간을 기다려야 합니다. 또한 에서 필요한 정보는 사실 그리 많지 않습니다. 학습에 영향을 주지 않는 정보들까지 메모리에 저장하는 것은 낭비입니다.
이런 문제를 해결하기 위하여 6 년뒤, Maaten 은 Barnes-hut tree 라는 vector indexing 방법을 이용하여 계산 비용을 줄인 방법을 제안합니다 (Maaten, 2014). 이 방법의 개념은 아래 그림과 같습니다. 처음에 원 공간을 작은 지역들로 나눠둡니다. 마치 서울시에 위치하는 사람들을 작은 지도로 옮기려 할 때, 먼저 서울시를 구들로 나누고 각 구를 동으로 나누어 사람들이 현재 어떤 (구, 동)에 위치하는지 인덱싱 합니다. 원 t-SNE 에서는 사람마다 한명씩 돌아가면서 임베딩 공간에서 위치를 잡아주지만, Barnes-hut 을 이용하는 t-SNE 에서는 동 단위로 사람을 움직입니다.
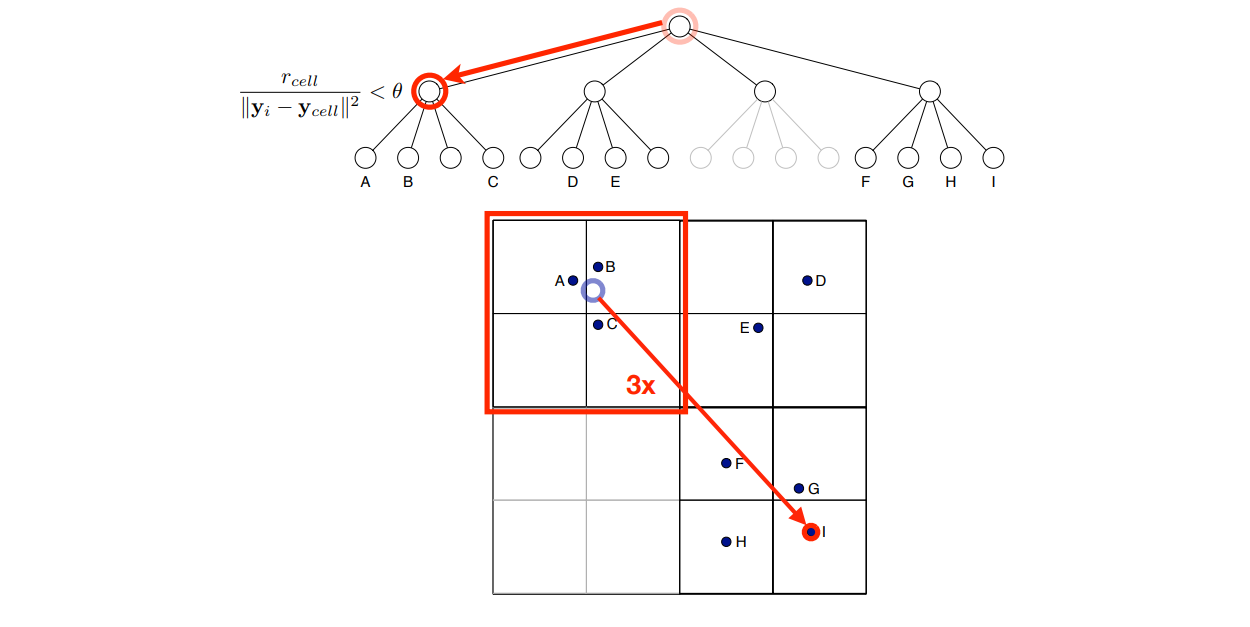
scikit-learn 의 구현체는 Barnes-hut tree 를 이용하고 있습니다. 다른 구현체에서 t-SNE 를 이용하실 때 어떤 버전의 t-SNE 인지 확인하시고 이용하시길 바랍니다.
Perplexity and locality
Perplexity 는 중요한 값입니다. t-SNE 는 임베딩 과정에서 영향을 많이 받는 nearest neighbors 와 그렇지 않은 점들을 칼처럼 자르지는 않습니다 (LLE 는 정확히 k 개의 이웃의 구조만 보존합니다). 대신, 두루뭉실하게 거리에 반비례하여 영향력을 정의합니다 (). 그리고 perplexity 는 어느 범위까지 영향력을 강하게 할지 정의하는 역할을 합니다.
Perplexity 는 로 정의됩니다. 그리고 entropy 는 확률 분포가 얼마나 예상하기 어려운가에 대한 지표입니다. 이는 다음처럼 정의됩니다.
만약 가 가능한 값이 0, 1, 2 이고 각각의 확률이 1/3 이라면 entropy 는 최대가 됩니다. 한 개의 숫자를 뽑았을 때 0, 1, 2 중 어떤 숫자가 뽑힐지 예상하기 어렵기 때문입니다. 대신 각각의 숫자의 확률이 (0.98, 0.01, 0.01) 이라면 한 번 숫자를 뽑았을 때 0 일 가능성이 매우 높습니다. 이처럼 어떤 숫자가 뽑힐지 쉽게 예상이 된다면 entropy 는 작습니다. 그리고 를 어떤 값으로 설정하느냐에 따라 의 perplexity 가 결정됩니다.
이를 위하여 간단한 실험을 해봅니다. 우리는 1,000 개의 데이터 간 거리를 임의로 만든 뒤 다양한 를 이용하여 를 만듭니다. 이 세 종류의 데이터는 points 가 아닌 distance 입니다. 그리고 이 distances 의 분포를 살펴봅니다. 첫번째는 한 점 를 기준으로 거리가 uniform distance 를 따른다고 가정합니다. 사실 이런 거리는 1 차원의 random samples 에서나 나타날 수 있는 거리 분포이긴 합니다. 두번째 데이터는 거리가 가까운 점들이 거리가 먼 점들보다 많은 경우입니다. 정확히 말하면, 아주 가까운 점 외에는 점들 간 거리가 고만고만한 경우입니다. 대체로 고차원 데이터에서 이러한 패턴이 보입니다. 마지막 데이터는 가까운 점들보다 거리가 먼 점들이 기하급수적으로 많아지는 데이터입니다. 2 ~ 5 차원 같은 저차원 데이터에서 이러한 패턴이 보입니다.
import numpy as np
n_data = 1000
# uniform
uniform = np.random.random_sample(n_data)
# leftside-skewed
leftskewed = uniform **(1.5)
# rightside-skewed
rightskewed = uniform ** (1/3)
dist_samples = [
uniform,
leftskewed,
rightskewed
]Bokeh 를 이용하여 거리 분포의 히스토그램을 그려봅니다. 그리고 세 데이터의 거리 히스토그램을 distance_figures 에 저장해둡니다. 를 만든 뒤 함께 gridplot 을 그려 살펴보기 위해서입니다.
distance_figures = []
for i, dist in enumerate(dist_samples):
hist, edges = np.histogram(dist, density=True, bins=20)
title = 'Data #{}'.format(i+1)
p = figure(background_fill_color="#E8DDCB", height=600, width=600, title=title)
p.quad(top=hist, bottom=0, left=edges[:-1], right=edges[1:],
fill_color="#036564", line_color="#033649")
distance_figures.append(p)
show(p)각 거리 샘플의 히스토그램은 아래와 같습니다.
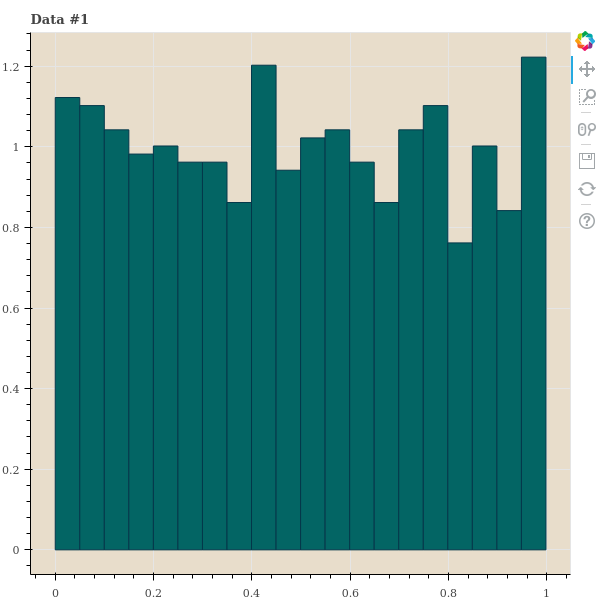
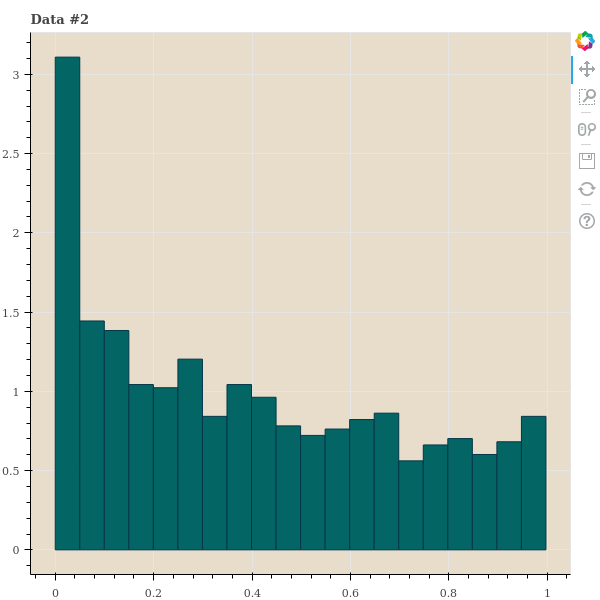
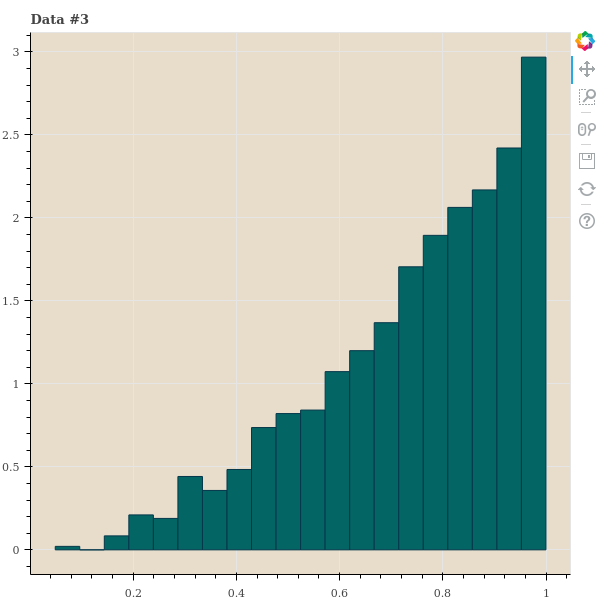
t-SNE 는 기대하는 perplexity 를 맞추는 를 찾기 위하여 binary search 를 합니다. 예를 들어 로 perplexity 를 계산하였더니 이 값이 너무 크다면 를 절반으로 나눠서 다시 계산하는 겁니다. 우리는 중간에 와 perplexity 의 변화를 살펴보기 위하여 verbose 도 추가하여 binary search 를 하는 함수를 만들어 봅니다. Binary search 를 할 때 perplexity 의 크기가 진동할 경우, 2 배수로 키우거나 줄이는 것을 1.8 배, 1.62 배 씩 키우거나 줄이도록 decay 기능을 넣어둡니다.
def get_entropy(dist_, var):
prob = to_prob(dist_, var)
entropy = - (prob * np.log(prob)).sum()
return entropy
def to_prob(dist_, var):
prob = np.exp(-(dist_.copy() ** 2) / var)
prob = prob / prob.sum()
return prob
def binary_search_variance(dist, perplexity=30.0, verbose=False):
desired_entropy = np.log2(perplexity)
var = 1
decay = 0.9
factor = 2
previous_diff_sign = True
for n_try in range(30):
entropy = get_entropy(dist, var)
entropy_diff = entropy - desired_entropy
diff_sign = entropy_diff > 0
if previous_diff_sign != diff_sign:
factor = max(1, factor * decay)
if entropy_diff > 0:
var /= factor
else:
var *= factor
if verbose:
print('var = {:f}, perplexity = {:f}'.format(var, 2 ** entropy))
previous_diff_sign = diff_sign
if factor == 1:
break
return var, 2 ** entropy테스트 삼아 첫 번째 distance sample 를 perplexity = 30 을 만족하는 를 찾아봅니다.
binary_search_variance(dist_samples[0], verbose=True)아래처럼 var = 1 로 시작하여 0.006915 까지 그 값을 줄여가며 perplexity 가 30 이 되도록 값을 찾습니다.
var = 0.500000, perplexity = 116.908883
var = 0.250000, perplexity = 109.963842
var = 0.125000, perplexity = 95.196686
var = 0.062500, perplexity = 76.614612
var = 0.031250, perplexity = 60.595323
var = 0.015625, perplexity = 48.178333
var = 0.007812, perplexity = 38.530957
var = 0.003906, perplexity = 30.862100
var = 0.007031, perplexity = 24.493020
var = 0.012656, perplexity = 29.825070
var = 0.007812, perplexity = 36.019429
var = 0.004823, perplexity = 30.862100
var = 0.007031, perplexity = 26.318585
var = 0.010252, perplexity = 29.825070
var = 0.007812, perplexity = 33.674926
var = 0.005954, perplexity = 30.862100
var = 0.007031, perplexity = 28.240360
var = 0.008304, perplexity = 29.825070
var = 0.007813, perplexity = 31.475196
var = 0.007350, perplexity = 30.862100
var = 0.006915, perplexity = 30.258543
var = 0.006915, perplexity = 29.664045
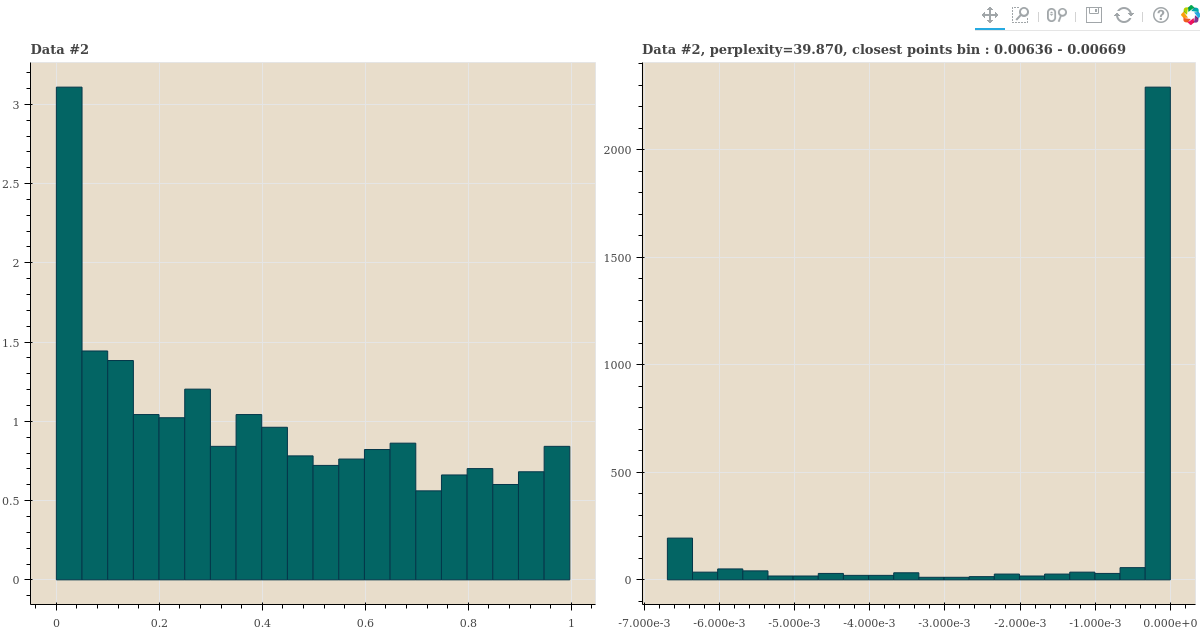
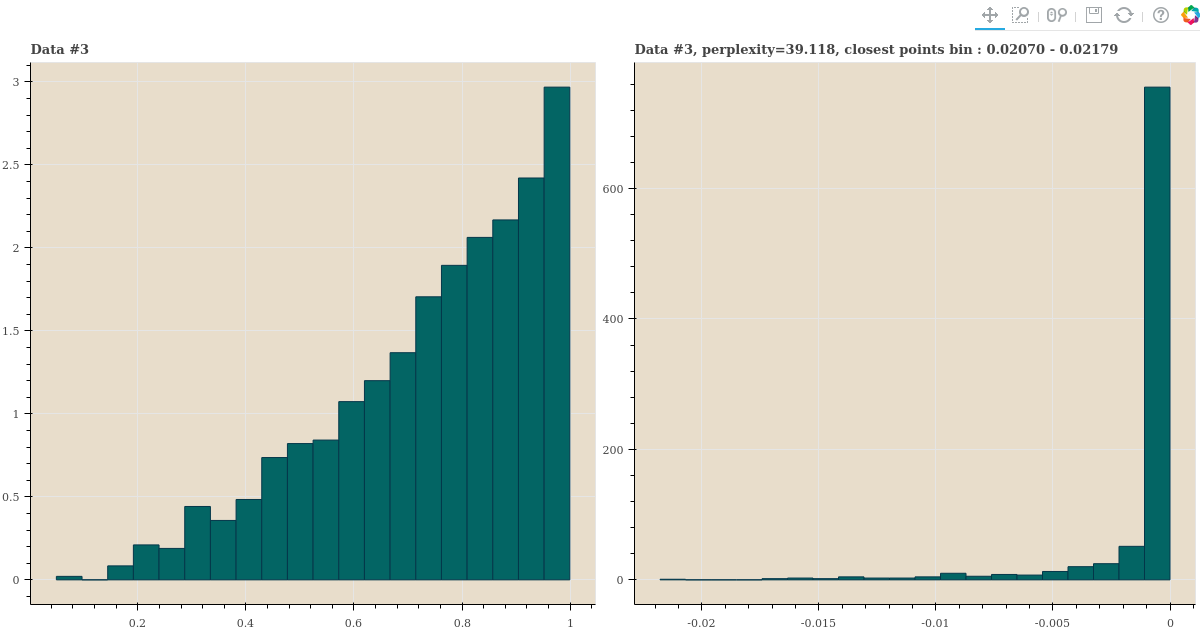
세 distance samples 의 perplexity 가 40 에 가깝게 되도록 를 찾은 뒤, 이 값으로 를 만듭니다. 그리고 이 값의 히스토그램을 plotting 합니다.
from bokeh.layouts import gridplot
for i, dist in enumerate(dist_samples):
var, perplexity = binary_search_variance(dist, perplexity=40)
prob = to_prob(dist, var)
hist, edges = np.histogram(-prob, density=True, bins=20)
title = 'Data #{}, perplexity={:.3f}, closest points bin : {:.5f} - {:.5f}'.format(
i+1, perplexity, -edges[1], -edges[0])
p = figure(background_fill_color="#E8DDCB", height=600, width=600, title=title)
p.quad(top=hist, bottom=0, left=edges[:-1], right=edges[1:],
fill_color="#036564", line_color="#033649")
gp = gridplot([distance_figures[i], p], ncols=2, title=title)
show(gp)histogram 을 역순으로 정렬하기 위하여 확률에 -1 을 곱하여 plots 을 그렸습니다. 오른쪽 그림의 좌측의 값이 가장 가까운 점들의 확률과 그 숫자입니다. 세 distance distribution 이 다름에도 불구하고 오른쪽 plots 들은 소수의 점들만 확률이 크며, 대부분의 점들은 확률이 거의 0 에 가깝습니다.
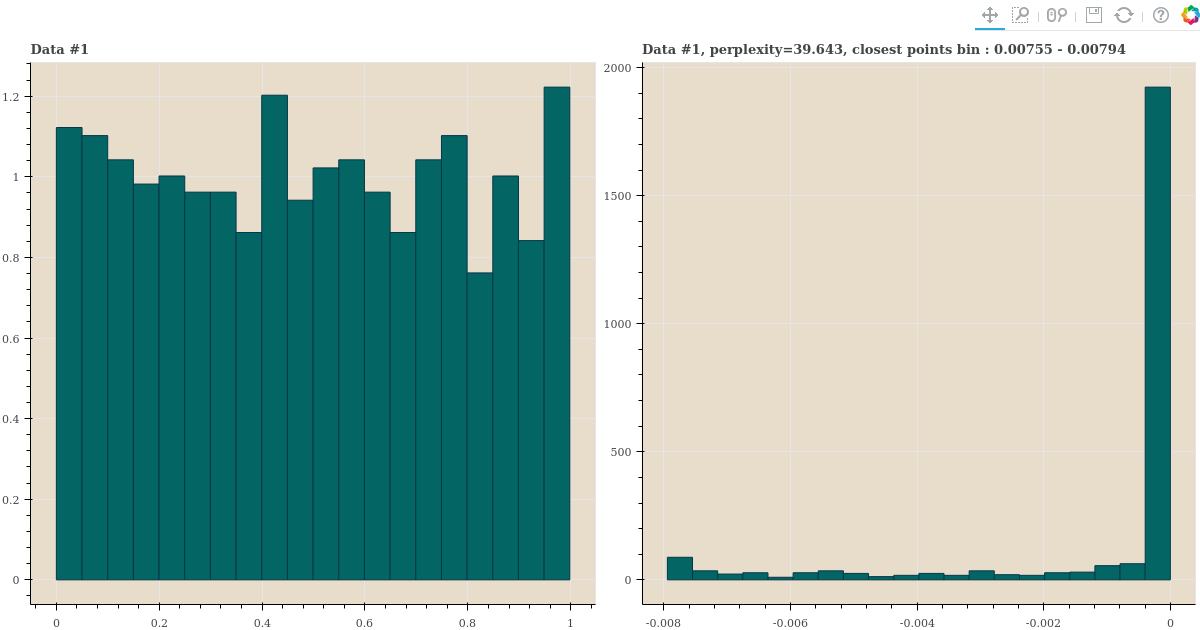
심지어 가까운 점들이 먼 점들보다 많은 경우에도 일부의 점들만 이 큽니다. 확률이 큰 점들이 유독 가까운 점들입니다.
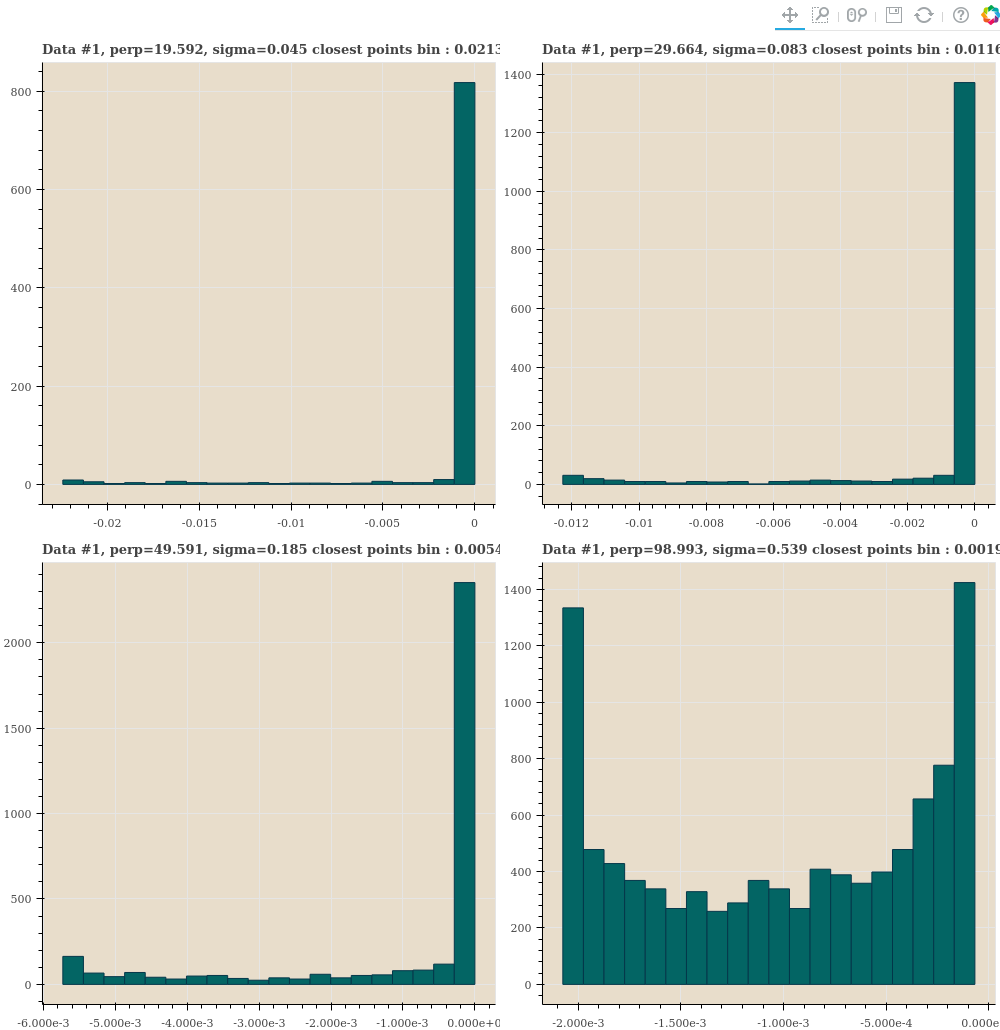
첫번째 distance samples 이 다양한 perplexity 를 만족하도록 를 찾고, 가장 가까운 점들의 도 살펴봅니다.
dist = dist_samples[0]
plots = []
for perplexity in [20, 30, 50, 100]:
var, perplexity = binary_search_variance(dist, perplexity=perplexity)
prob = to_prob(dist, var)
hist, edges = np.histogram(-prob, density=True, bins=20)
title = 'Data #1, perp={:.3f}, closest points bin : {:.5f} - {:.5f}'.format(
perplexity, -edges[1], -edges[0])
p = figure(background_fill_color="#E8DDCB", height=500, width=500, title=title)
p.quad(top=hist, bottom=0, left=edges[:-1], right=edges[1:],
fill_color="#036564", line_color="#033649")
plots.append(p)
gp = gridplot([[plots[0], plots[1]], [plots[2], plots[3]]])
show(gp)Perplexity 가 작을수록 가장 가까운 점들의 bins 의 probability 는 크고 는 작습니다. 가 작을수록 의 값은 커집니다. 그리고 점들 간의 의 값은 아주 가까운 점을 제외하고는 매우 작은 값이 됩니다. Exponential 은 과 는 차이가 크지만 과 은 차이가 거의 없기 때문입니다.
작은 는 locality 를 강조합니다. 이 때는 의 분포가 한 쪽으로 크게 치우칩니다. 반대로 큰 는 모든 점들 간의 유사도를 비슷하게 만듭니다. 그렇기 때문에 점들 간의 는 큰 차이가 나지 않고 모두들 작은 확률값을 나눠 가집니다.
| Perplexity | range of first bin | |
|---|---|---|
| 19.59 | 0.045 | 0.0213 - 0.0224 |
| 29.66 | 0.083 | 0.0117 - 0.0123 |
| 49.59 | 0.185 | 0.0054 - 0.0057 |
| 98.99 | 0.539 | 0.00198 - 0.00208 |
Plotting 을 하여 살펴보면 perplexity 가 커질수록 대부분의 점들이 작은 값의 비슷한 확률을 지니고, perplexity 가 작을수록 몇 몇 점들만 큰 probability 를 대부분은 아주 작은 probability 를 지님을 볼 수 있습니다. 즉 는 locality boundary 를 조절하는 parameter 입니다.
앞서 t-SNE 는 locality 뿐 아니라 global structure 를 모두 고려한다는 말을 하였습니다. 논문이 추구하는 바이기도 하고요. 하지만 실제 구현 시에는 지나치게 작은 는 무시합니다. 의 차이에 의한 학습보다 truncation error 에 의한 오류가 더 클 수도 있을 정도이기 때문입니다. 즉 t-SNE 도 사실상 locality 만 고려합니다. 그러나 그 local 의 boundary 가 LLE 의 most closest k points 처럼 hard boundary 가 아닌, 확률에 의하여 정의되는 soft boundary 일 뿐입니다.
앞서 세 종류의 distance distribution 에 동일한 perplexity 를 적용했을 때 대체로 비슷한 경향을 보입니다. 확률이 큰 bins 에 해당하는 점들의 개수가 작고 대부분은 0 에 가까운 확률을 지닙니다. 즉, distance distribution 에 관계없이 대체로 비슷한 모양의 를 만듭니다. 즉 각 점마다 다른 점들과의 거리 분포를 일정하게 만들어버리는 것입니다. 이러한 non-linear transformation 을 위하여 non-linear 함수인 exponential 이 이용되었습니다. 물론 data 3 처럼 가까운 점들이 매우 적은 경우에는 가까운 점들의 확률이 상대적으로 커지긴 합니다만, 분포의 모습이 변하진 않습니다. 그렇기 때문에 distance distribution 에 robust 한 임베딩 결과를 학습할 수 있습니다.
그리고 마지막 실험에서 살펴본 것처럼 지나치게 크거나 작은 perplexity 만 아니면 대체로 비슷한 임베딩 모습을 보여줍니다. 즉 parameter robust 한 임베딩 학습 결과를 보여줄 수 있습니다.
How to select perplexity
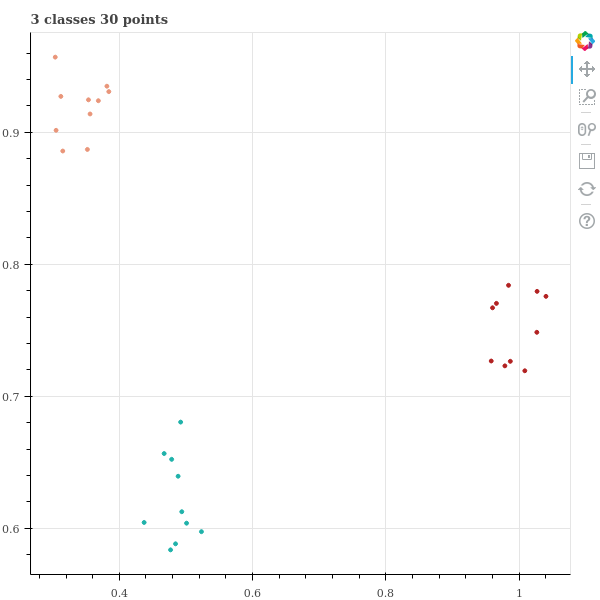
그렇다면 지나치게 크거나 작은 perplexity 의 기준을 알아야 합니다. 이를 위해서 또 다른 실험을 해봅시다. 3 개의 클래스 별로 10 개의 점들을 만듭니다.
n_data_per_class = 10
n_classes = 3
x = []
y = []
for c in range(n_classes):
x_ = 0.1 * np.random.random_sample((n_data_per_class, 2))
x_ += np.random.random_sample((1, 2))
x.append(x_)
y.append(np.asarray([c] * n_data_per_class))
x = np.vstack(x)
y = np.concatenate(y)점들은 클래스 별로 조금씩 떨어진 군집을 형성하고 있습니다.
title = '{} classes {} points'.format(n_classes, n_classes * n_data_per_class)
p = figure(width=600, height=600, title=title)
colors = 'firebrick darksalmon lightseagreen'.split()
for c in range(n_classes):
idx = np.where(y == c)[0]
x_ = x[idx]
p.scatter(x_[:,0], x_[:,1], fill_color=colors[c], line_color=colors[c])
show(p)세 군집이 명확히 구분됨을 scatter plot 으로 확인할 수 있습니다.
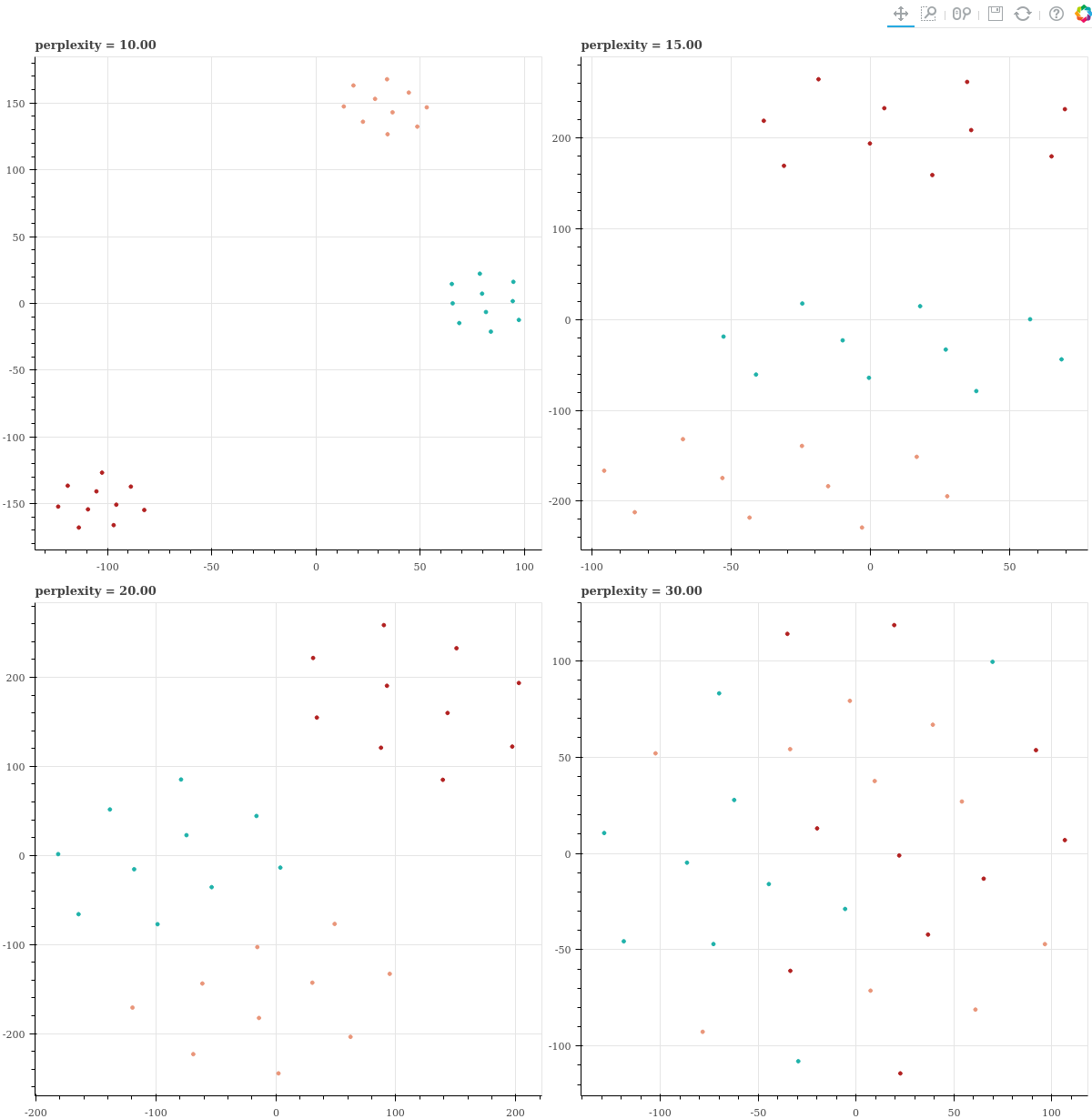
이 데이터에 대하여 perplexity 를 [10, 15, 20, 30] 으로 늘려가며 t-SNE 를 학습하고, 그 결과를 scatter plots 으로 확인합니다.
from sklearn.manifold import TSNE
grids = []
for perplexity in [10, 15, 20, 30]:
p = figure(width=600, height=600, title='perplexity = {:.2f}'.format(perplexity))
z = TSNE(n_components=2, perplexity=perplexity).fit_transform(x)
for c in range(n_classes):
idx = np.where(y == c)[0]
z_ = z[idx]
p.scatter(z_[:,0], z_[:,1], fill_color=colors[c], line_color=colors[c])
grids.append(p)
gp = gridplot([[grids[0], grids[1]], [grids[2], grids[3]]])
show(gp)Perplexity 가 10 일 때에는 세 군집이 여전히 잘 분리가 되어 임베딩이 됩니다. 하지만 perplexity 가 커질수록 조금씩 군집 간 경계가 모호해지고, perplexity 가 지나치게 크게 되면 군집간 경계가 사라져 모든 점들이 뒤섞입니다. 특히 perplexity = 30 일 때에는 임베딩된 점들 간의 거리가 등간격이 됩니다. 이 패턴은 데이터의 개수가 작은데 perplexity 가 지나치게 크기 때문에 이를 맞추기 위하여 가 과하게 커졌기 때문입니다. 모든 점들 간의 가 균등해질 때 perplexity 가 최대가 될 수 있기 때문입니다.
즉, 아래의 perplexity = 30 처럼 점들 간 간격이 균등한 그림이 그려진다면 데이터의 개수가 지나치게 작을 때 입니다. 이 때에는 perplexity 를 작게 조절하면 됩니다.
Distance metrics
t-SNE 는 를 계산하기 전에 모든 에 대하여 pairwise distance 를 계산합니다. 이 때 Euclidean distance 를 이용하는데, bag-of-words model 과 같이 sparse vector 로 표현된 데이터라면 Euclidean distance 보다는 Cosine distance 나 Jaccard distance 가 더 적절합니다. 0.19.0 부터 scikit-learn 의 t-SNE 도 Cosine distance 를 이용할 수 있습니다. TSNE 를 만들 때 metric 만 변경하면 됩니다.
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, metric='cosine')
y = tsne.fit_transform(x)Discussion
위 그림들만 살펴보면 t-SNE 도 perplexity 에 따라 상이한 학습 결과가 보이기 때문에, parameter sensitive 한 알고리즘으로 생각할 수 있습니다. 그러나 LLE, MDS, ISOMAP 과 같은 알고리즘과 시각화 결과를 비교해보면 t-SNE 가 (상대적으로) 얼마나 안정적인 임베딩 학습 결과를 보여주는 지 알 수 있습니다. 뒤이은 포스트에서 다른 알고리즘과의 임베딩 결과의 비교를 해보겠습니다.
그리고, 모든 알고리즘이 그렇듯이 t-SNE 도 절대 만능이 아닙니다. 어떤 경우에 t-SNE 가 학습에 실패할 가능성이 높은지에 대해서도 따로 알아보겠습니다.
References
- Van der Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(2579-2605), 85.
- L.J.P. van der Maaten. (2014), Accelerating t-SNE using Tree-Based Algorithms. Journal of Machine Learning Research 15(Oct):3221-3245