(initializer, update rules, grid size) Self Organizing Map (SOM) 은 1980 년대에 고차원 벡터 공간의 2차원 시각화를 위하여 제안된 뉴럴 네트워크 입니다. 오래된 방법이지만 살펴볼 점들이 충분히 많은 알고리즘입니다. 최근 고차원 벡터 시각화를 위해 이용할 수 있는 t-SNE 나 PCA 의 단점을 개선하는 방법을 찾던 중, SOM 을 개선하면 특정 목적에 맞는 훌륭한 시각화 방법을 만들 수 있겠다는 생각을 하였습니다. 성능을 개선하기 위해서는 우선 알고리즘의 작동 원리와 특징을 알아야 합니다. 이번 포스트에서는 SOM 을 직접 구현하며, 특징을 이해하고 잠재적 위험성을 알아봅니다.
Self Organizing Map
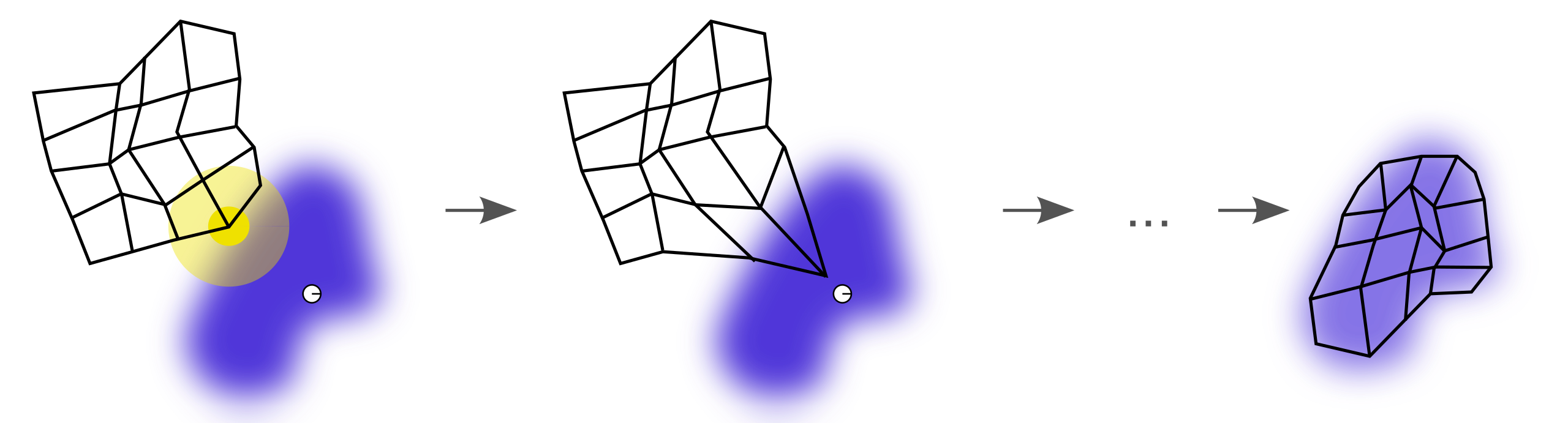
아래의 위키피디아 그림은 SOM 의 작동 원리를 가장 잘 설명한 그림이라 생각합니다. SOM 의 목적은 고차원의 벡터를 시각화 할 수 있는 2차원의 저차원으로 표현하는 것입니다. 그 2차원 공간은 주로 격자 (grid) 로 표현됩니다. 아래 그림은 (5, 5) 크기의 격자이며, 파란색은 고차원 데이터 공간에서의 밀도입니다. 하얀색 점은 현재의 학습데이터의 한 포인트이며, 격자 점 중 현재의 포인트와 가장 가까운 점과 그 주변 점들이 학습데이터에 점점 가까워지면서 결국은 세번째 그림처럼 격자가 데이터 공간을 학습합니다. 고차원의 벡터는 격자 좌표인 (0, 0) 부터 (4, 4) 의 2차원 좌표값으로 표현됩니다.
물론 2차원 공간의 모습을 정방형의 격자로 한정하지는 않습니다. 임의의 어떤 형태로도 2차원 공간을 마련할 수 있지만, 직사각형의 종이/화면 위에 지도를 그린다면 공간의 낭비가 없는 직사각형 형태의 격자 (rectangular grid) 가 가장 효율적일 것입니다. 그 외에도 육각형으로 이뤄진 격자 (hexagonal grid) 를 이용할 수도 있습니다. 이도 rectangular grid 와 다른 장단점이 있는데, 이는 다른 포스트에서 다뤄봅니다.
SOM 의 학습 원리는 다음과 같습니다. 1단계로, 격자를 생성하고 학습 데이터와 같은 크기인 input_dim 차원의 벡터값을 할당합니다. 격자의 (0, 0) 를 0 번 마디라 하며, C[0,0] 의 벡터값을 지닙니다. 그리고 마디 0 은 마디 1, 마디 5와 인접합니다.
import numpy as np
n_data = 1000
input_dim = 10
X = np.random.random_samples((n_data, input_dim))
n_rows, n_cols = 5, 5
n_codes = n_rows * n_cols
grid = np.arange(n_codes).reshape(n_rows, n_cols)
C = np.random.random_sample((n_codes, input_dim))
print(grid)
[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
2단계로 모든 데이터 \(X_i\) 에 대하여 각각 가장 가까운 격자 위 마디 \(u\) 를 찾습니다. \(t\) 는 현재의 학습 시간 (epoch) 을 의미합니다. 가장 가까운 마디를 SOM 에서는 best matching unit (BMU) 라 부릅니다. 그리고 그 마디와 인접한 이웃 마디들을 함께 해당 데이터 방향으로 조금 이동시킵니다. BMU 의 주변 마디 \(v\) 도 업데이트가 이뤄지지만, \(X_i\) 와 가장 가까운 \(u\) 보다는 적은 양을 업데이트 합니다. BMU 와 그 이웃 간의 업데이트 비율에 차등을 두는 가중치를 \(\theta(u, v, t)\) 로 기술합니다. 일종의 mask 와 같은 기능입니다. 조금 이동시키기 위하여 learning rate, \(\alpha(t)\) 를 곱합니다. 학습이 지속되면 마디의 벡터값이 수렴하기 때문에 학습 시간에 따라서 learning rate 를 줄이는 방법이 이용되기도 하기 때문에 \(\alpha(t)\) 처럼 기술합니다. 마디의 벡터 값이 이동할 방향은 현재의 학습데이터에서 마디 벡터를 뺀 벡터 방향입니다. 이를 수식으로 표현하면 아래와 같습니다.
\[W_v(t+1) = W_v(t) + \theta(u, v, t) \cdot \alpha(t) \cdot (X_i - W_v(t))\]마디의 벡터값 \(W\), 코드에서의 C 는 (n_codes, input dim) 크기의 행렬입니다. 그리고 이는 1 layer feed forward 뉴럴 네트워크로 해석할 수 있습니다. 이 layer 를 지나면 입력데이터가 (0.5, 0.35) 와 같은 2 차원의 좌표값으로 변환되기 때문입니다. 학습 데이터의 모든 점들에 대하여 각각 업데이트가 일어나기 때문에 stochastic gradient descent 방식입니다. gradient 는 마디와 현재 데이터 간의 차이인 \(X_i - W_v(t)\) 입니다. 이 과정을 최대 반복 횟수 epochs 혹은 \(W_v\) 가 수렴할 때까지 반복합니다. \(W_v\) 는 계속하여 데이터 \(X_i\) 에 가까워지기 때문에 학습이 끝나면 학습 데이터에 있을 법한 벡터값이 할당되어 있습니다.
SOM 의 학습 방식을 주로 competitive learning 이라 부릅니다. 일반적인 feed forward 뉴럴 네트워크는 하나의 데이터에 의하여 gradient 가 발생하면 hidden layer 의 모든 값에 영향을 줍니다. 하지만 SOM 에서는 \(X_i\) 와 가장 가까운 \(u\) 그리고 그 이웃인 \(v\) 까지만 gradient 가 업데이트 됩니다. Competitive learning 은 데이터에 따라 학습되는 부분이 다르게 정의된다는 의미입니다. 이와 동시에 coorperative learning 라고도 합니다. \(X_i\) 에 의하여 단 하나의 마디 (혹은 a hidden unit) 만 학습하지 않고, 그 주변 마디들을 함께 학습하기 때문입니다.
Coorperative 한 부분이 SOM 의 가장 큰 특징입니다. 만약 BMU 외 다른 인접한 마디들을 학습하지 않는다면 위 식은 n_codes 개의 군집을 학습하는 k-means 의 minibatch 버전입니다. k-means 를 학습할 때 각 군집들은 서로 독립적입니다. 한 군집의 centroid 가 학습될 때 다른 군집들이 영향을 주지 않습니다. 하지만 SOM 은 사전에 군집을 초기화 하면서 0 번과 1, 5 번 군집은 서로 비슷한 군집이라는 사전 지식을 모델에 입력하였고, 실제로 학습을 할 때에도 0 번 마디가 이동하면 이와 인접한 1, 5 번 마디가 함께 이동하여 군집 간 인접 구조가 유지되도록 만듭니다. 이 부분이 grid 가 고차원 공간의 2 차원 지도 역할을 하도록 만듭니다. 마디 0 과 1 이 비슷한 벡터를 지니기 때문에 BMU 가 0 인 \(X_i\) 와 BMU 가 1 인 \(X_j\) 는 원 공간에서도 비슷할 가능성이 높기 때문입니다.
이번 포스트에서는 이러한 개념적인 내용들을 직접 코드로 구현하여 눈으로 확인해 봅니다. 이 포스트는 numpy 와 scikit-learn 만을 이용하여 SOM 을 구현하였으며, 데이터 시각화를 위해서는 Bokeh >= 1.4.0 을 이용합니다.
Dataset
작은 인공데이터를 만들어 개발에 이용합니다. soydata 는 알고리즘 개발에 이용할 인공 데이터를 생성하는 함수들이 포함되어 있습니다. 이 패키지는 아래의 레포지토리에서 다운받아 설치할 수 있습니다.
git clone https://github.com/lovit/synthetic_dataset
cd synthetic_dataset
python setup.py install
soydata 에는 데이터 생성 함수 및 scatter plot 과 line plot 을 그리는 함수를 포함하였습니다. 이들을 import 합니다. 또한 numpy.ndarray 의 깔끔한 print 를 위한 show_matrix 라는 유틸 함수도 만들어 둡니다. Bokeh 는 IPython notebook 에서 그림을 그릴 경우에 bokeh.plotting.output_notebook() 을 실행해야 합니다. 그런데 이 패키지에서 3 차원 scatter plot 을 그리기 위하여 Plotly 도 함께 이용하고 있습니다. 이 둘 패키지의 IPython notebook 에서의 사용을 모두 준비하기 위하여 use_notebook 이라는 함수를 따로 마련해 두었습니다.
import numpy as np
import soydata
from soydata.visualize import use_notebook
use_notebook()
def show_matrix(array):
with np.printoptions(precision=3, suppress=True):
print(array)
데이터를 생성하고 이를 scatter plot 으로 그립니다. n_clusters=8 이지만, 세 개의 군집이 약간 겹쳐져 있기 때문에 5 개의 군집으로 이뤄진 모습입니다. Random seed 를 seed=0 으로 고정하였기 때문에 이 코드를 실행할 때마다 동일한 데이터가 생성됩니다. 구현체가 제대로 작동하는지 확인하기 위하여 개발 과정에서는 2차원 데이터만을 이용합니다. 이 데이터는 103 개의 2차원 벡터값으로 구성되어 있습니다.
from soydata.data.clustering import make_rectangular_clusters
from soydata.visualize import scatterplot, lineplot
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
p = scatterplot(X, height=600, width=600, title='Dataset', color='lightgrey')
Simple initializer of grid and mask
간단한 초기화 함수를 만듭니다. make_grid_and_neighbors 함수는 격자는 행, 열의 개수 n_rows, n_cols 가 주어지면 이를 이용하여 직사각형 형태의 grid 를 만들고, grid 내에서 가로나 세로로 인접한 마디들을 pairs 에 저장합니다. 우리는 학습데이터가 2차원이라는 사실을 아니 initialize_simple 함수에서 격자의 행, 열의 개수가 주어지면, x, y 축에 0 부터 1 사이의 값을 각각 등간격으로 나눠 (np.linspace) 격자의 마디의 벡터값 C 을 초기화 합니다.
def initialize_simple(n_rows, n_cols):
# make grid and neighbor index
grid, pairs = make_grid_and_neighbors(n_rows, n_cols)
# initialize coordinate of grid nodes
x_ranges = np.linspace(0, 1, n_rows)
y_ranges = np.linspace(0, 1, n_cols)
C = np.asarray([[x, y] for x in x_ranges for y in y_ranges])
return grid, C, pairs
def make_grid_and_neighbors(n_rows, n_cols):
grid = np.arange(n_rows * n_cols).reshape(n_rows, n_cols)
pairs = []
for i in range(n_rows):
for j in range(n_cols):
idx = grid[i,j]
neighbors = []
if j > 0:
neighbors.append(grid[i,j-1])
if i > 0:
neighbors.append(grid[i-1,j])
for nidx in neighbors:
pairs.append((idx, nidx))
return grid, pairs
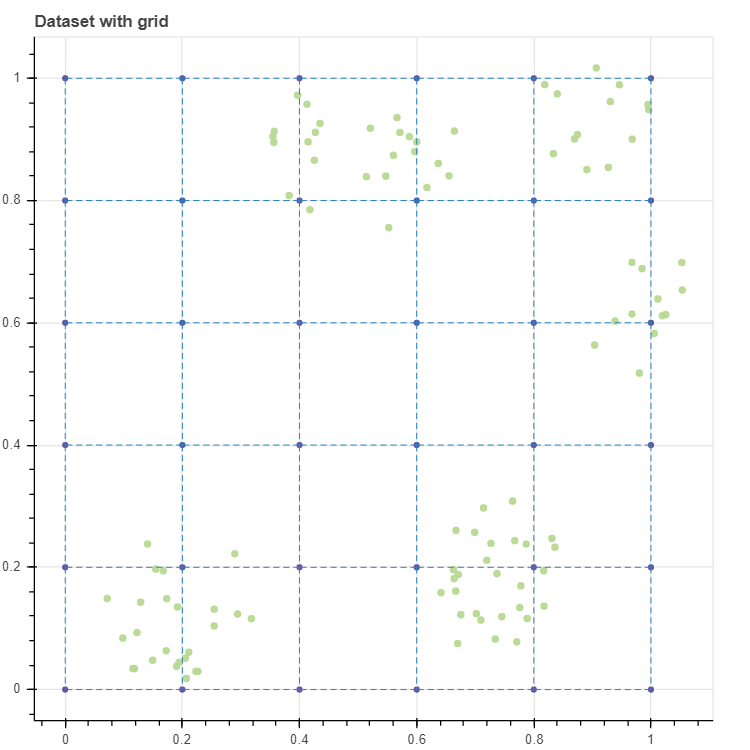
위 함수를 이용하여 (6, 6) 크기의 격자를 생성합니다. 아래 코드의 두 개의 scatterplot 에는 show_inline=False 로 설정하였는데, 이는 p 에 그림을 중첩하여 그리기 위한 설정입니다. 기본값은 show_inline=True 로 이를 변경하지 않으면 scatterplot 이나 lineplot 을 실행할 때마다 그림이 그려집니다. 그리고 그림을 중첩하기 위하여 두번째와 세번째 plot 함수에는 p=p 로 이전에 그린 그림 p 를 함수 인자로 입력하였습니다. 0 부터 1 까지 0.2 간격으로 이뤄진 (6, 6) 의 격자가 만들어졌습니다.
n_rows = 6
n_cols = 6
metric = 'euclidean'
grid, C, pairs = initialize_simple(n_rows, n_cols)
p = scatterplot(X, height=600, width=600, color='lightgrey', title='Dataset with grid', size=3, alpha=0.5, show_inline=False)
p = scatterplot(C, p=p, size=4, show_inline=False)
p = lineplot(C, p=p, pairs=pairs, line_width=0.5)
이번에는 위 식의 \(\theta(u, v, t)\) 인 한 마디 \(u\) 와 인접한 마디 \(v\) 의 가중치를 미리 설정해둡니다. 이를 구현하는 방식은 다양할텐데 이번에는 마스크 (mask) 처럼 구현합니다. make_gaussian_mask 함수는 grid 가 입력되면 grid[i,j] 와 Manhattan distance 가 max_width 보다 가까운 마디들에 대하여 거리에 반비례하는 가중치를 부여합니다.
make_masks 는 모든 마디 grid[i,j] 에 대하여 마스크를 구현하는 함수입니다. 여기서 sorted_indices 를 이용하여 행과 열을 정렬하는 부분이 있는데, 이 부분의 쓰임새는 아래에서 예시로 확인합니다. 그리고 make_gaussian_mask 는 grid 와 같은 크기의 행렬을 return 하지만 make_masks 는 column vector 형식으로 flatten 된 벡터열을 return 합니다. 이는 이후 행렬 계산의 편리함을 위해서입니다.
def make_masks(grid, sigma=1.0, max_width=2):
rows, cols = np.where(grid >= 0)
data = grid[rows,cols]
sorted_indices = data.argsort()
indices = zip(rows[sorted_indices], cols[sorted_indices])
masks = [make_gaussian_mask(grid, i, j, sigma, max_width) for i,j in indices]
masks = [mask.flatten() for mask in masks]
return masks
def make_gaussian_mask(grid, i, j, sigma=1.0, max_width=2):
mask = np.zeros(grid.shape)
for i_, j_ in zip(*np.where(grid >= 0)):
if (max_width > 0) and (abs(i - i_) + abs(j - j_) > max_width):
continue
mask[i_,j_] = np.exp(-((i-i_)**2 + (j-j_)**2) / sigma**2)
return mask
show_matrix(make_gaussian_mask(grid, 2, 3))
make_gaussian_mask 함수를 이용하여 (2, 3) 와 주위 마디의 가중치를 확인합니다. show_matrix 함수는 numpy.ndarray 의 값을 소수점 3번째 자리까지만 출력해줍니다.
[[0. 0. 0. 0.018 0. 0. ]
[0. 0. 0.135 0.368 0.135 0. ]
[0. 0.018 0.368 1. 0.368 0.018]
[0. 0. 0.135 0.368 0.135 0. ]
[0. 0. 0. 0.018 0. 0. ]
[0. 0. 0. 0. 0. 0. ]]
make_masks 함수로 만든 masks 에서 grid[2,3] 에 해당하는 마스크를 확인합니다. (36,) 크기의 column vector 입니다.
idx = grid[2,3] # 15
masks = make_masks(grid)
print(masks[idx].shape)
show_matrix(masks[idx])
(36,)
[0. 0. 0. 0.018 0. 0. 0. 0. 0.135 0.368 0.135 0.
0. 0.018 0.368 1. 0.368 0.018 0. 0. 0.135 0.368 0.135 0.
0. 0. 0. 0.018 0. 0. 0. 0. 0. 0. 0. 0. ]
reshape 을 이용하면 앞서 살펴본 모양과 동일한 형태의 마스크를 확인할 수 있습니다.
show_matrix(masks[idx].reshape(n_rows, n_cols))
[[0. 0. 0. 0.018 0. 0. ]
[0. 0. 0.135 0.368 0.135 0. ]
[0. 0.018 0.368 1. 0.368 0.018]
[0. 0. 0.135 0.368 0.135 0. ]
[0. 0. 0. 0.018 0. 0. ]
[0. 0. 0. 0. 0. 0. ]]
앞서 make_masks 함수에서 행렬을 정렬하였는데, 이는 아래처럼 grid 내 마디의 인덱스가 정렬되지 않은 경우에도 이용하기 위함입니다.
grid_random = np.random.permutation(n_rows * n_cols).reshape(n_rows, n_cols)
grid_random
array([[30, 6, 16, 33, 21, 2],
[ 9, 35, 26, 1, 17, 27],
[10, 12, 24, 31, 11, 29],
[15, 23, 0, 5, 13, 8],
[ 7, 19, 3, 34, 4, 18],
[20, 28, 22, 14, 32, 25]])
위 그리드에서 마디 30 은 (0, 0) 에 위치합니다. make_masks 를 이용하여 만든 masks 에서 이에 해당하는 마스크를 확인하면 (0, 0) 과 그 주변 마디들에 가중치가 부여되어 있음을 확인할 수 있습니다. 이처럼 정렬 기능을 준비한 이유는 이후에 다룰 Growing SOM 에서는 그리드가 임의의 순서로 확장하여 인덱스가 정렬되지 않기 때문입니다.
masks_random = make_masks(grid_random)
show_matrix(masks_random[30].reshape(n_rows, n_cols))
[[1. 0.368 0.018 0. 0. 0. ]
[0.368 0.135 0. 0. 0. 0. ]
[0.018 0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0. ]]
Update using stochastic gradient descent
초기화 함수는 준비가 되었으니 업데이트 함수 부분을 구현해 봅니다. scikit-learn 의 pairwise_distances_argmin_min 함수는 X 의 모든 열마다 C 중에서 가장 가까운 열의 인덱스와 거리값을 탐색합니다. 이를 이용하여 closest 라는 함수를 만듭니다. Stochastic gradient descent 방식은 학습데이터의 모든 점에 대하여 각각 모델을 업데이트 합니다. 이때 학습데이터의 순서에 따라 모델의 패러매터가 진동할 수 있으니 매번 데이터의 순서를 섞어줍니다 (shuffle). 그 뒤 Xi 에 대하여 bmu 를 탐색하고 이 값과 현재의 마디 벡터값인 C_new 와의 차이를 계산합니다. diff 는 (n_codes, input dim) 크기의 행렬입니다. 여기에 (n_codes,) 크기의 masks[bmu] 를 곱합니다. 우리가 하고 싶은 것은 Xi - C 의 각 행에 해당하는 마스크의 값이 곱해지는 것이지만, 두 행렬의 차원이 맞지 않습니다. 이때는 numpy.newaxis 를 이용하면 됩니다.
from sklearn.metrics import pairwise_distances_argmin_min
def closest(X, C, metric):
# return (idx, dist)
return pairwise_distances_argmin_min(X, C, metric=metric)
def update_stochastic(X, C, lr=0.01, metric='euclidean', masks=None):
n_data = X.shape[0]
n_codes, n_features = C.shape
C_new = C.copy()
# shuffle data
Xr = X[np.random.permutation(n_data)]
for i, Xi in enumerate(Xr):
bmu, _ = closest(Xi.reshape(1,-1), C_new, metric)
bmu = int(bmu) # matrix shape=(0,)
diff = Xi - C_new # shape = (n_codes, n_features)
grad = lr * diff * masks[bmu][:,np.newaxis]
C_new += grad
return C_new
Stochastic gradient descent 방식의 업데이트 함수가 만들어졌으니 learning rate lr=0.1 로 설정하여 한 번 학습을 진행합니다.
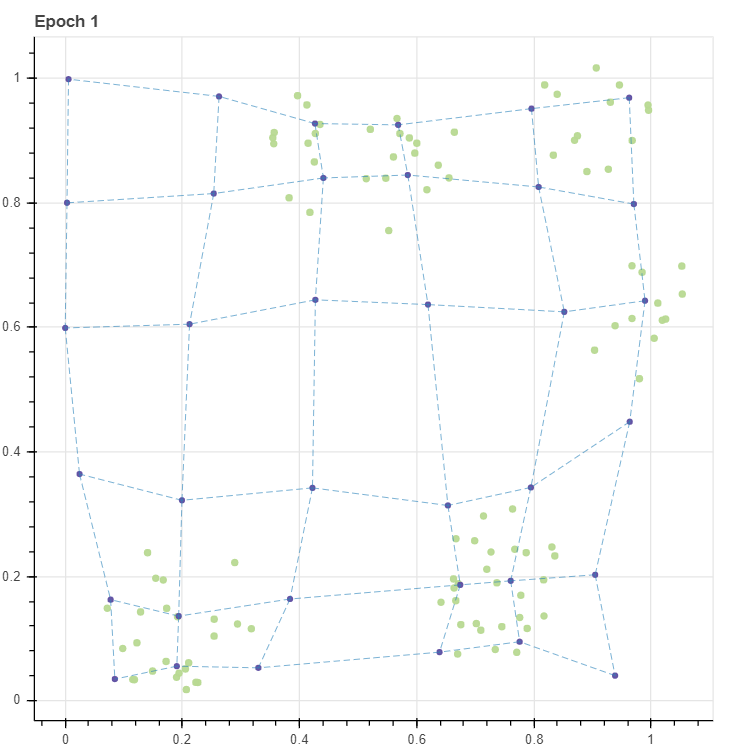
C_new = update_stochastic(X, C, lr=0.1, masks=masks)
p = scatterplot(X, height=600, width=600, color='lightgrey', title='Epoch 1', size=3, alpha=0.5, show_inline=False)
p = scatterplot(C_new, p=p, size=4, show_inline=False)
p = lineplot(C_new, p=p, pairs=pairs, line_width=0.5)
그 결과를 확인하면 격자가 데이터와 조금 더 가까워졌음을 확인할 수 있습니다.
이번에는 학습을 100 번 반복합니다. 매 10 번의 반복마다 마디의 벡터값의 변화 diff 도 확인합니다. 반복을 할수록 diff 값이 약간 감소하였습니다. 즉 값이 수렴하고 있다는 의미입니다. 하지만 수렴성이 눈에 띄지는 않습니다. 사실 이는 learning rate 가 데이터의 개수에 비하여 너무 크기 때문입니다. 여하튼 diff 를 계산할 수 있으니 early-stop 기능도 구현할 수 있습니다.
from sklearn.metrics.pairwise import paired_distances
C_old = C.copy()
epochs = 100
for epoch in range(epochs):
C_new = update_stochastic(X, C_old, lr=0.1, masks=masks)
diff = paired_distances(C_new, C_old, metric=metric).mean()
C_old = C_new
if epoch % 10 == 0:
print(f'epoch= {epoch}/{epochs}, diff={diff:.4}')
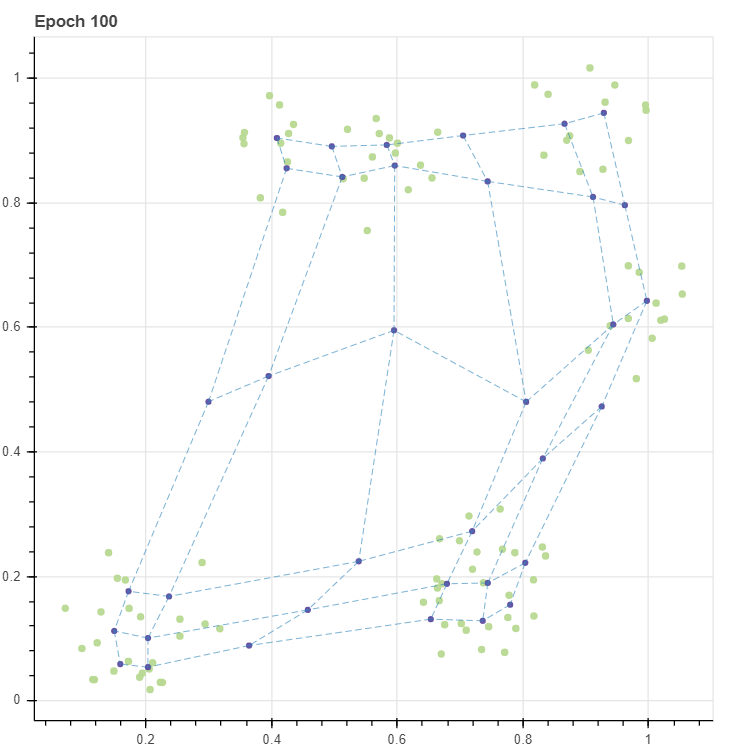
p = scatterplot(X, height=600, width=600, color='lightgrey', title=f'Epoch {epochs}', size=3, alpha=0.5, show_inline=False)
p = scatterplot(C_new, p=p, size=4, show_inline=False)
p = lineplot(C_new, p=p, pairs=pairs, line_width=0.5)
epoch= 0/100, diff=0.05978
epoch= 10/100, diff=0.005818
epoch= 20/100, diff=0.003774
epoch= 30/100, diff=0.003392
epoch= 40/100, diff=0.00249
epoch= 50/100, diff=0.00299
epoch= 60/100, diff=0.002851
epoch= 70/100, diff=0.003002
epoch= 80/100, diff=0.003113
epoch= 90/100, diff=0.003003
100 번의 반복 후 격자를 살펴보면 다섯 개의 군집 근처에 격자점들이 주로 분포함을 확인할 수 있습니다. 즉 (6,6) 의 격자는 103 개의 데이터의 분포를 닮도록 학습되었습니다.
그런데 저는 SOM 이 고차원 데이터 시각화에 유용할 수 있다고 생각되는 부분은 맨 좌측 가운데의 점을 학습한다는 것입니다. 좌측 하단에서 상단으로 올라가는 좌표는 (0,0), (0,1), .. 입니다. (0,3) 과 (1,3) 은 데이터가 존재하는 공간이 아닙니다. 고차원 공간의 시각화에 중요한 점 중 하나는 빈 공간을 학습하는 것입니다. 그러나 고차원 공간의 시각화에 자주 이용되는 t-SNE 는 빈 공간을 학습하는 능력이 없습니다. t-SNE 는 모든 점들을 2차원 공간에 “빈틈없이” 평평히 펼쳐 놓기 위한 방법입니다. 다음으로 자주 이용되는 PCA 는 빈 공간을 학습하는 능력이 있습니다만, 직교하는 두 개의 축에 대해서만 그 점들을 학습할 수 있습니다. 또한 고차원이지만, 사실상 저차원의 manifold 를 지닐 때에만 이러한 빈 공간이 잘 학습됩니다. 그러나 아래 그림에서 SOM 은 데이터가 존재하지 않는 공간에 대해서도 grid 가 학습을 합니다. 또한 (0,3) 은 (0,2), (0,4) 와 인접하기 때문에 (0,2) 와 (0,4) 사이에 빈 공간이 존재한다는 사실을 알 수 있습니다. 이처럼 원 공간에서 인접한 점들이 새로운 공간에서도 인접한 경우를 topological properties 가 보존되었다고 표현합니다. 물론 (0,3) 에 빈 공간이 학습된 것은 우연입니다. 데이터의 개수와 그리드 내 마디의 개수, 그리고 마디의 초기값이 절묘하게 조화를 이뤘기 때문이며, 항상 빈 공간이 학습되지는 않습니다. 이는 다음 포스트에서 더 자세히 다루겠습니다.
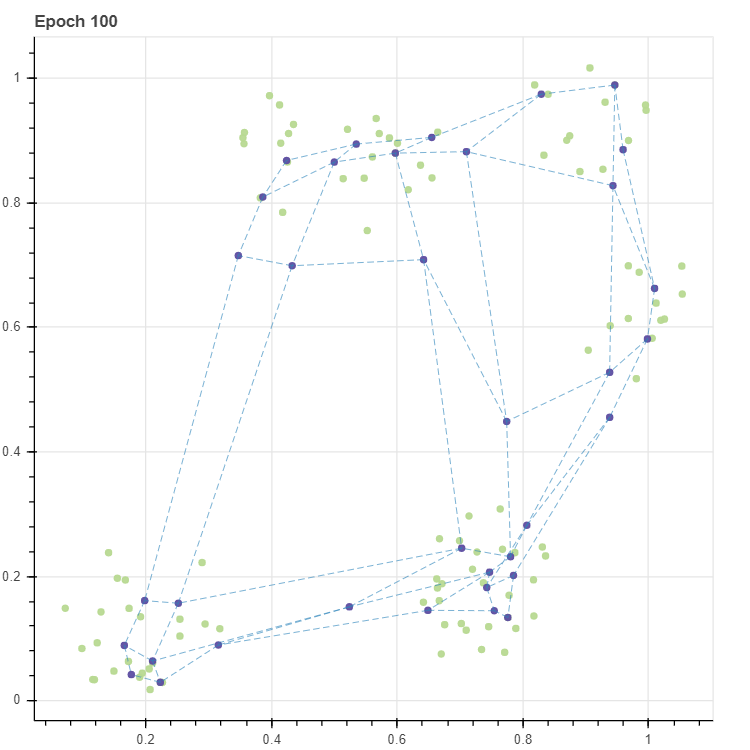
다시 SOM 개발로 돌아와서 이번에는 동일한 작업을 더 큰 learning rate, lr=1.0 으로 수행합니다. 일단 diff 가 이전에 비해 약 20 배 정도 큽니다. 마디값이 매우 크게 진동하고 있습니다.
C_old = C.copy()
epochs = 100
for epoch in range(epochs):
C_new = update_stochastic(X, C_old, lr=1.0, masks=masks)
diff = paired_distances(C_new, C_old, metric=metric).mean()
C_old = C_new
if epoch % 10 == 0:
print(f'epoch= {epoch}/{epochs}, diff={diff:.4}')
p = scatterplot(X, height=600, width=600, color='lightgrey', title=f'Epoch {epochs}', size=3, alpha=0.5, show_inline=False)
p = scatterplot(C_new, p=p, show_inline=False)
p = lineplot(C_new, p=p, pairs=pairs, line_width=0.5)
epoch= 0/100, diff=0.1427
epoch= 10/100, diff=0.07342
epoch= 20/100, diff=0.0749
epoch= 30/100, diff=0.0856
epoch= 40/100, diff=0.07526
epoch= 50/100, diff=0.05645
epoch= 60/100, diff=0.06516
epoch= 70/100, diff=0.07926
epoch= 80/100, diff=0.07929
epoch= 90/100, diff=0.05995
결과를 살펴보면 그리드가 삐툴어졌습니다. learning rate = 1.0 은 \(X_i - C\) 의 값을 그대로 gradient 로 이용한다는 의미입니다. \(W_v\) 가 \(X_i\) 로 한번에 가까워지고, 다른 데이터 \(X_j\) 에 의하여 다시 멀리 흐트러진다는 의미입니다. 그래서 learning rate 를 작게 유지해야 합니다. 이는 일반적인 뉴럴 네트워크의 학습의 상식과도 일맥상통합니다. 그러나 어떤 값을 이용해야 하는지는 알 수 없습니다. 하지만 학습이 진행될수록 마디값이 수렴한다면 반복 횟수가 증가함에 따라 작은 learning rate 를 이용해야 할 것입니다.
앞서 구현한 stochastic gradient descent 함수와 반복 횟수에 따른 learning rate 의 조절 기능을 포함하여 fit 함수로 정리합니다. 이때 masks 와 업데이트 함수인 update_stochastic 를 keyword arguments, **kargs 에 입력하였습니다. 이는 이후 fit 함수를 다른 방식의 업데이트 함수와 함께 이용하기 위한 준비입니다.
import math
from time import time
def fit(X, C, epochs, metric='euclidean', lr=0.1, decay=True,
epsilon=0.00001, verbose=10, epoch_begin=0, **kargs):
update_func = kargs.get('update_func', update_stochastic)
C_old = C.copy()
t = time()
lr_e = lr
eb = epoch_begin
for e in range(eb, epochs + eb):
# update
C_new = update_func(X, C_old, lr_e, metric, **kargs)
diff = paired_distances(C_new, C_old, metric=metric).mean()
C_old = C_new
# verbose
if (verbose > 0) and (e % verbose) == 0:
print(f'epoch= {e}/{epochs}, diff={diff:.4}')
# check whether satisfy earlystop condition
if diff < epsilon:
print(f'Early stop at {e}/{epochs}')
break
# decaying learning rate
if decay:
lr_e = lr * (1 - 0.5 * (e + 1) / epochs)
t = time() - t
t_epoch = t / (e+1)
if verbose > 0:
print(f'Training time = {t:.3} sec; {t_epoch:.3}/epoch sec')
return C_old, t, e
이제 학습 함수까지 정리를 하였으니 이를 모두 이용하여 데이터를 생성, 네트워크를 초기화, 학습을 완료한 뒤 그 결과를 시각화합니다.
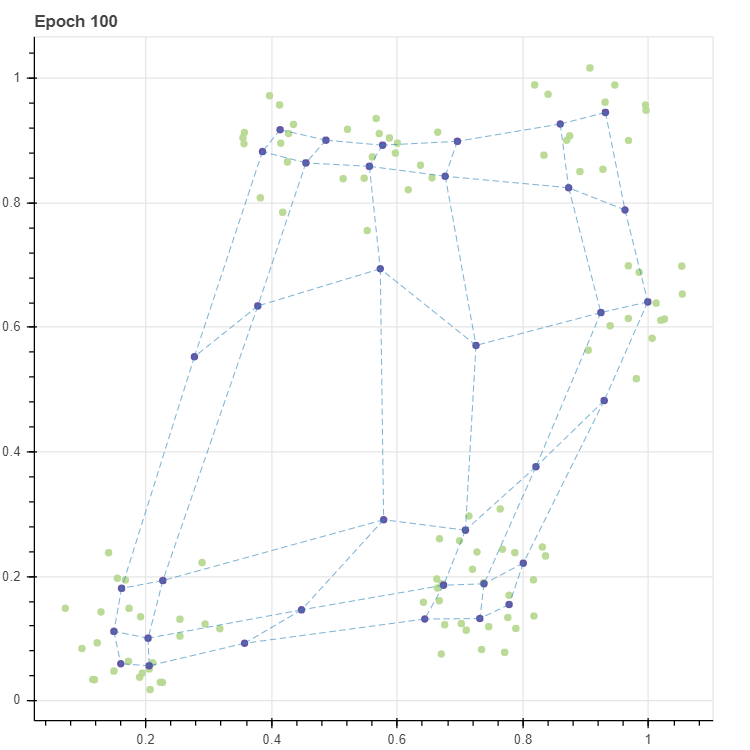
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
grid, C, pairs = initialize_simple(6, 6)
C_new, _, _ = fit(X, C, epochs=100, masks=masks, lr=0.1, decay=True)
p = scatterplot(X, height=600, width=600, color='lightgrey', title=f'Epoch {epochs}', size=3, alpha=0.5, show_inline=False)
p = scatterplot(C_new, p=p, show_inline=False)
p = lineplot(C_new, p=p, pairs=pairs, line_width=0.5)
epoch= 0/100, diff=0.06047
epoch= 10/100, diff=0.00552
epoch= 20/100, diff=0.003811
epoch= 30/100, diff=0.002412
epoch= 40/100, diff=0.001813
epoch= 50/100, diff=0.001478
epoch= 60/100, diff=0.001427
epoch= 70/100, diff=0.001194
epoch= 80/100, diff=0.001054
epoch= 90/100, diff=0.0008535
Training time = 2.84 sec; 0.0284/epoch sec
앞서 확인했던 그림과 동일한 그리드가 학습되었습니다.
Drawing plots for debugging
그런데 학습 도중의 그리드 상태를 scatter plots 로 모아서 보면 좋을 것 같습니다. 매번 원하는 epochs 수 만큼 학습을 진행하고 scatter plot 으로 그린 뒤, 이를 figures 에 저장합니다. 그리고 list 형식인 figures 를 list of list 로 만들어 Bokeh 의 gridplot 을 만듭니다. Bokeh 의 grid plot 에 대한 설명과 사용법은 이전의 Bokeh tutorial 을 보시기 바랍니다.
from bokeh.layouts import gridplot
def fit_with_draw(X, C, epochs, metric='euclidean', lr=0.11, decay=True,
epsilon=0.00001, verbose=10, n_fig_cols=3, draw_each=10, **kargs):
# Initialize figure list
figures = []
if isinstance(draw_each, int):
num_figs = math.ceil(epochs / draw_each)
epochs_array = [draw_each for b in range(num_figs)]
else:
epochs_array = draw_each
# draw initial condition
p = scatterplot(X, height=400, width=400, color='lightgrey', title='Initialize', show_inline=False)
p = scatterplot(C, p=p, size=4, show_inline=False)
p = lineplot(C, p=p, pairs=pairs, line_width=0.5, show_inline=False)
figures.append(p)
# fit and draw
C_new = C.copy()
base = 0
for epoch_this in epochs_array:
# fit
C_new, _, _ = fit(X, C_new, epoch_this, metric, lr, decay,
epsilon, verbose=epochs, epoch_begin=base, **kargs)
# draw
title = f'Epoch {base + epoch_this}'
p = scatterplot(X, height=400, width=400, color='lightgrey', title=title, show_inline=False)
p = scatterplot(C_new, p=p, size=4 if C.shape[0] <= 64 else 3, show_inline=False)
p = lineplot(C_new, p=p, pairs=pairs, line_width=0.5, show_inline=False)
figures.append(p)
# update base
base += epoch_this
# make grid plot
figure_mat = []
n_figs = len(figures)
for b in range(0, n_figs, n_fig_cols):
figure_mat.append(figures[b : b + n_fig_cols])
gp = gridplot(figure_mat)
return gp
위에서 만든 fit_with_draw 함수를 이용하여 epochs=100 학습 시 매 20 번마다 현재의 그리드 상태를 scatter plot 으로 그려 grid plot 으로 return 합니다. 그리고 bokeh.plotting.show 함수를 이용하여 이를 출력합니다. 그런데 이후부터는 이 포스트에서는 learning rate 를 학습 반복 횟수에 따라 감소하는 decay 를 이용하지 않습니다. 수렴도 제대로 이뤄지지 않는데 억지로 지나치게 작은 크기의 learning rate 를 이용할 필요는 없기 때문입니다.
from bokeh.plotting import show
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
gp = fit_with_draw(X, C, epochs=100, masks=masks, draw_each=20, epsilon=-0.1, decay=False)
show(gp)
Training time = 0.583 sec; 0.0291/epoch sec
Training time = 0.52 sec; 0.013/epoch sec
Training time = 0.482 sec; 0.00803/epoch sec
Training time = 0.481 sec; 0.00602/epoch sec
Training time = 0.481 sec; 0.00481/epoch sec
약 20 번의 학습으로도 그리드는 적절한 수준으로 수렴하였습니다. SOM 의 학습은 데이터 근처에 있는 마디들이 데이터에 달라붙고, 그 뒤 주변의 데이터와 떨어진 마디들이 천천이 옮겨붙는 패턴으로 이뤄집니다.
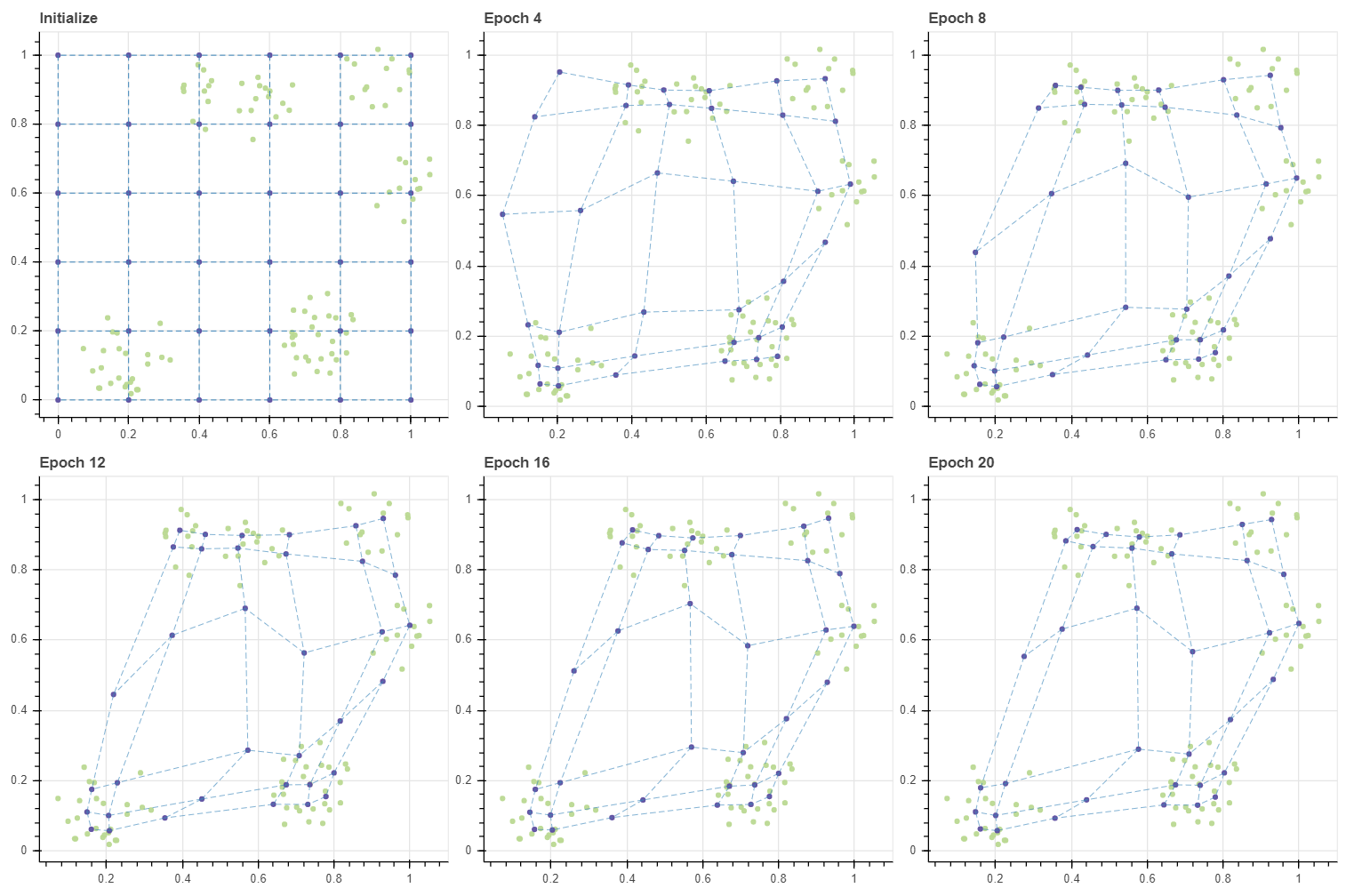
Training SOM with large grid
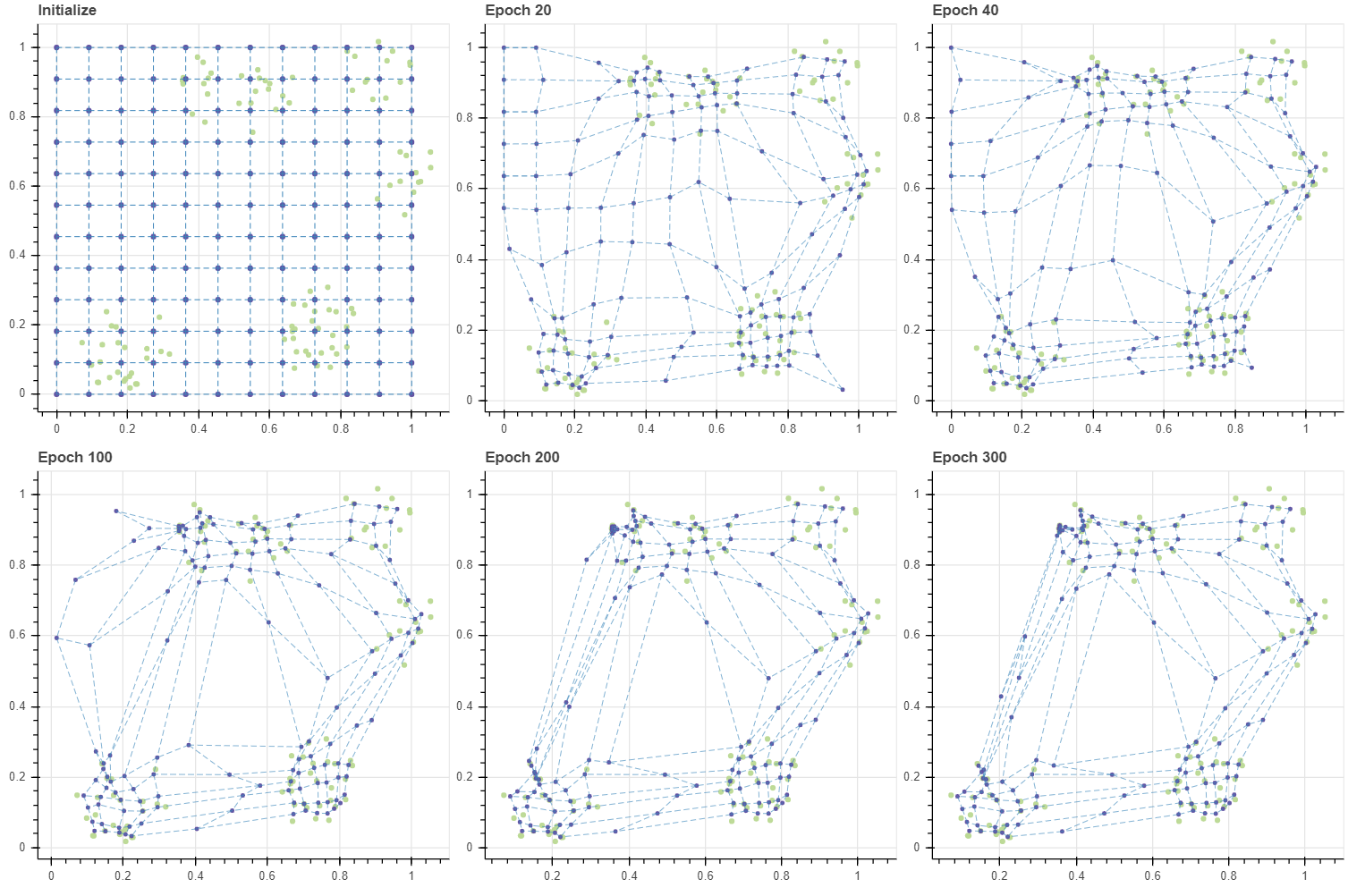
이번에는 그리드 내 마디의 개수를 훨씬 많이 증가시켜 봅니다. (12,12) 크기의 격자에는 144 개의 마디가 있습니다. 이는 데이터의 개수, 103 보다도 큽니다. 필요한 반복 횟수는 늘어났지만, 학습은 (6,6) 그리드처럼 수렴합니다. 그리고 빈 공간도 일부 학습이 되었습니다. 학습 초기를 더 자세히 살펴보기 위하여 동일한 간격의 epoch 이 아닌, 임의의 반복 횟수를 draw_each 에 입력할 수 있도록 하였습니다. 편리하군요. 이제 계속 세팅만 바꿔가며 여러가지를 실험해 볼 수 있습니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
grid, C, pairs = initialize_simple(12, 12)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=300, masks=masks,
draw_each=[20, 20, 60, 100, 100], epsilon=-0.1, decay=False)
위에서도 공통된 패턴이 발견되는데, 학습이 진행될수록 epoch 당 학습 시간이 줄어듭니다. 이는 gradient 의 값이 0 에 가까워지면 행렬 값의 곱셈과 덧셈이 일부 일어나지 않기 때문이라 짐작됩니다.
Training time = 0.573 sec; 0.0286/epoch sec
Training time = 0.497 sec; 0.0124/epoch sec
Training time = 1.5 sec; 0.015/epoch sec
Training time = 2.48 sec; 0.0124/epoch sec
Training time = 2.49 sec; 0.00829/epoch sec
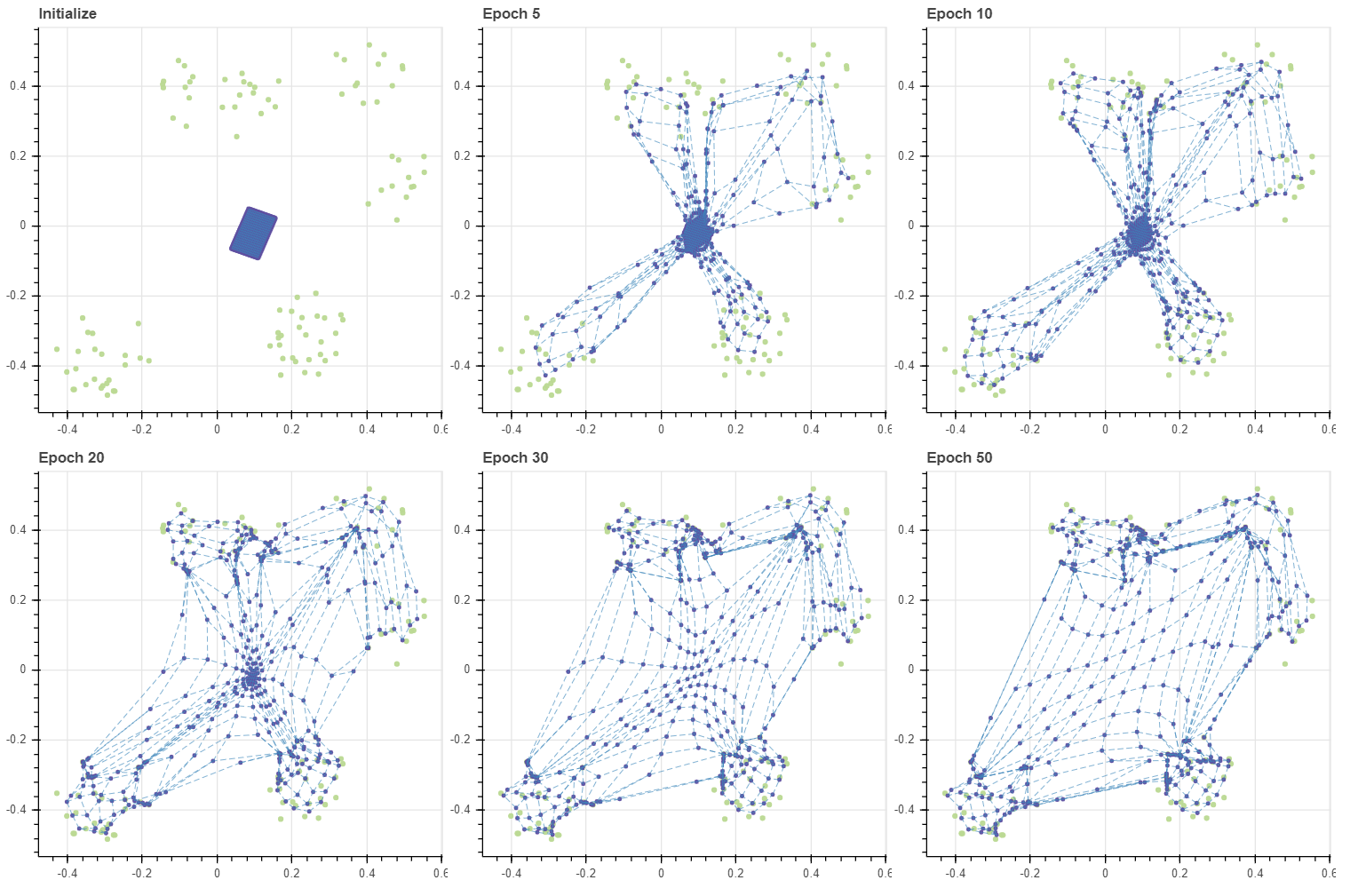
앞서 SOM 의 학습 패턴은 데이터 근처의 마디들이 우선적으로 데이터에 달라붙고, 그 뒤 주변 마디가 천천히 옮겨온다고 말하였습니다. BMU 에 해당하는 마디들은 빠르게 데이터 주변으로 이동하지만, 한 번도 BMU 로 선택되지 못한 마디들은 학습데이터에 의하여 직접적으로 업데이트가 일어나는 것이 아니라, 주변 이웃 마디가 BMU 였기 때문에 “덤”으로 업데이트가 이뤄집니다. 그리고 이 부분은 SOM 의 약점입니다.
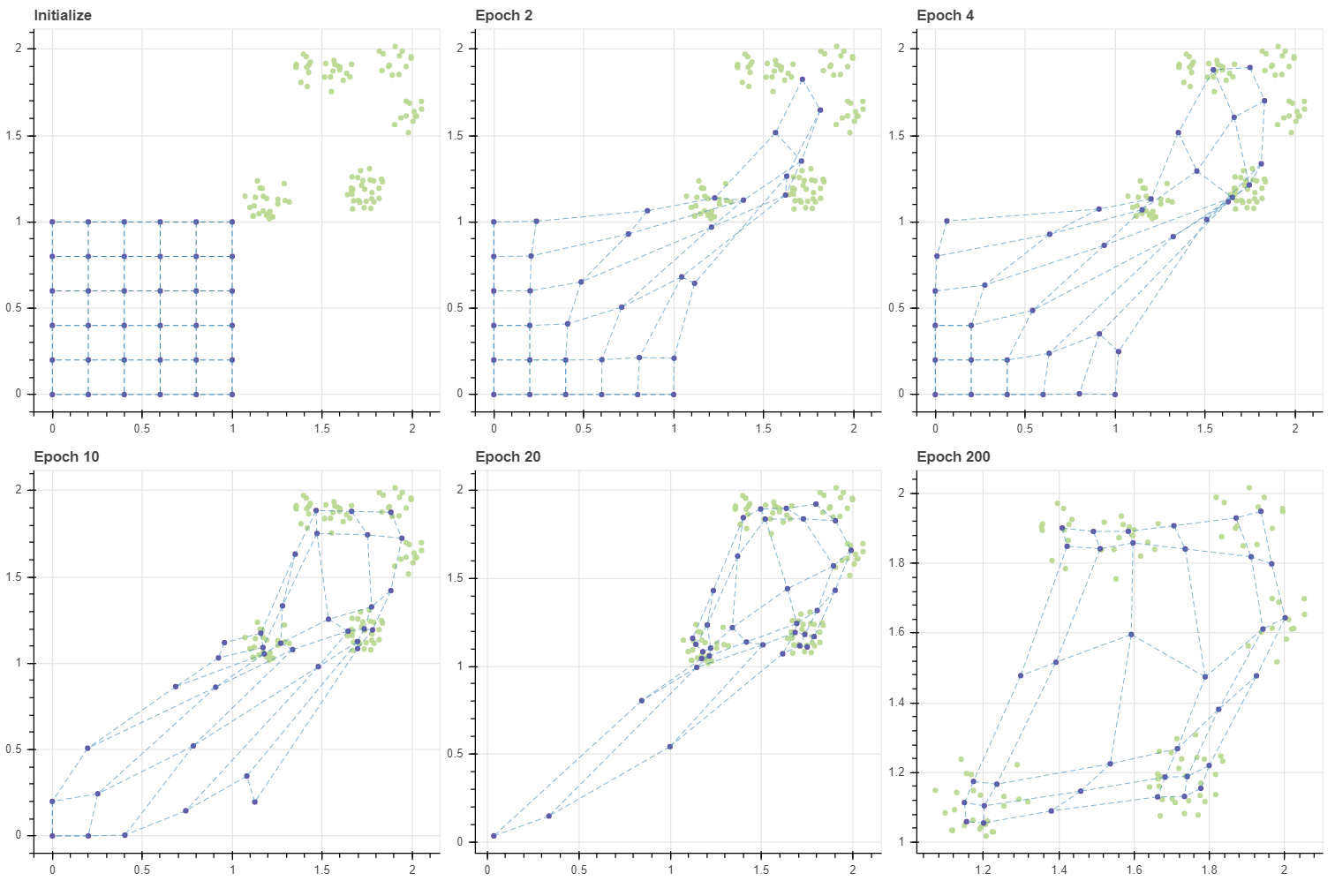
Out-ranged initial points
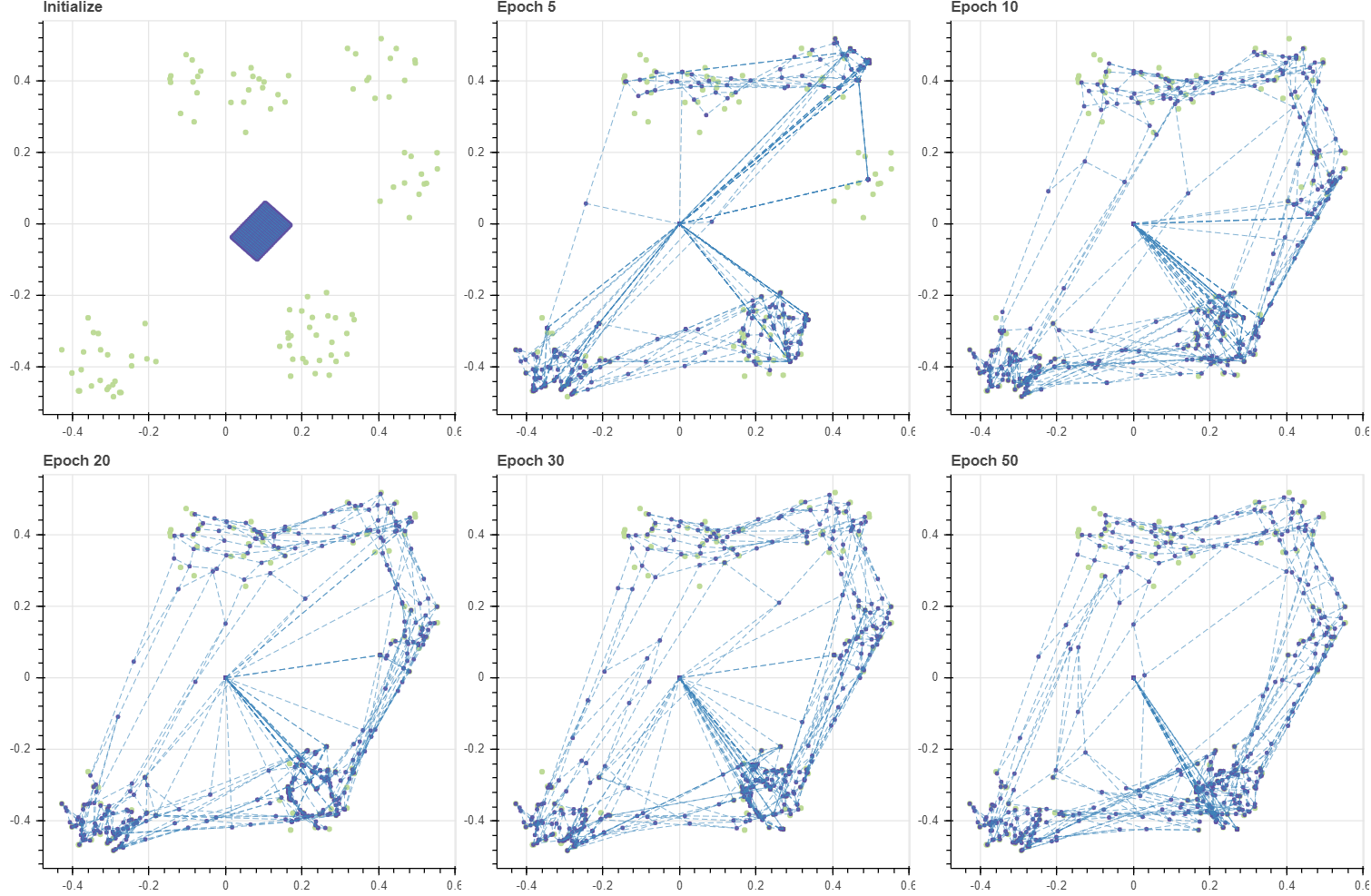
우리는 무심하게 마디의 초기값으로 (0, 1) 사이의 값을 이용하였지만, 마디의 초기값에 따라 SOM 의 학습 속도와 성능은 달라집니다. 아래는 데이터의 범위를 (1,1) 부터 (2,2) 옮기고, (6,6) 크기의 그리드의 초기값은 그대로 (0,0) 부터 (1,1) 을 이용한 경우입니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
X += 1.0
grid, C, pairs = initialize_simple(6, 6)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=200, masks=masks,
draw_each=[2, 2, 6, 10, 180], epsilon=-0.1, decay=False)
show(gp)
Training time = 0.0795 sec; 0.0397/epoch sec
Training time = 0.0565 sec; 0.0141/epoch sec
Training time = 0.17 sec; 0.017/epoch sec
Training time = 0.281 sec; 0.0141/epoch sec
Training time = 4.34 sec; 0.0217/epoch sec
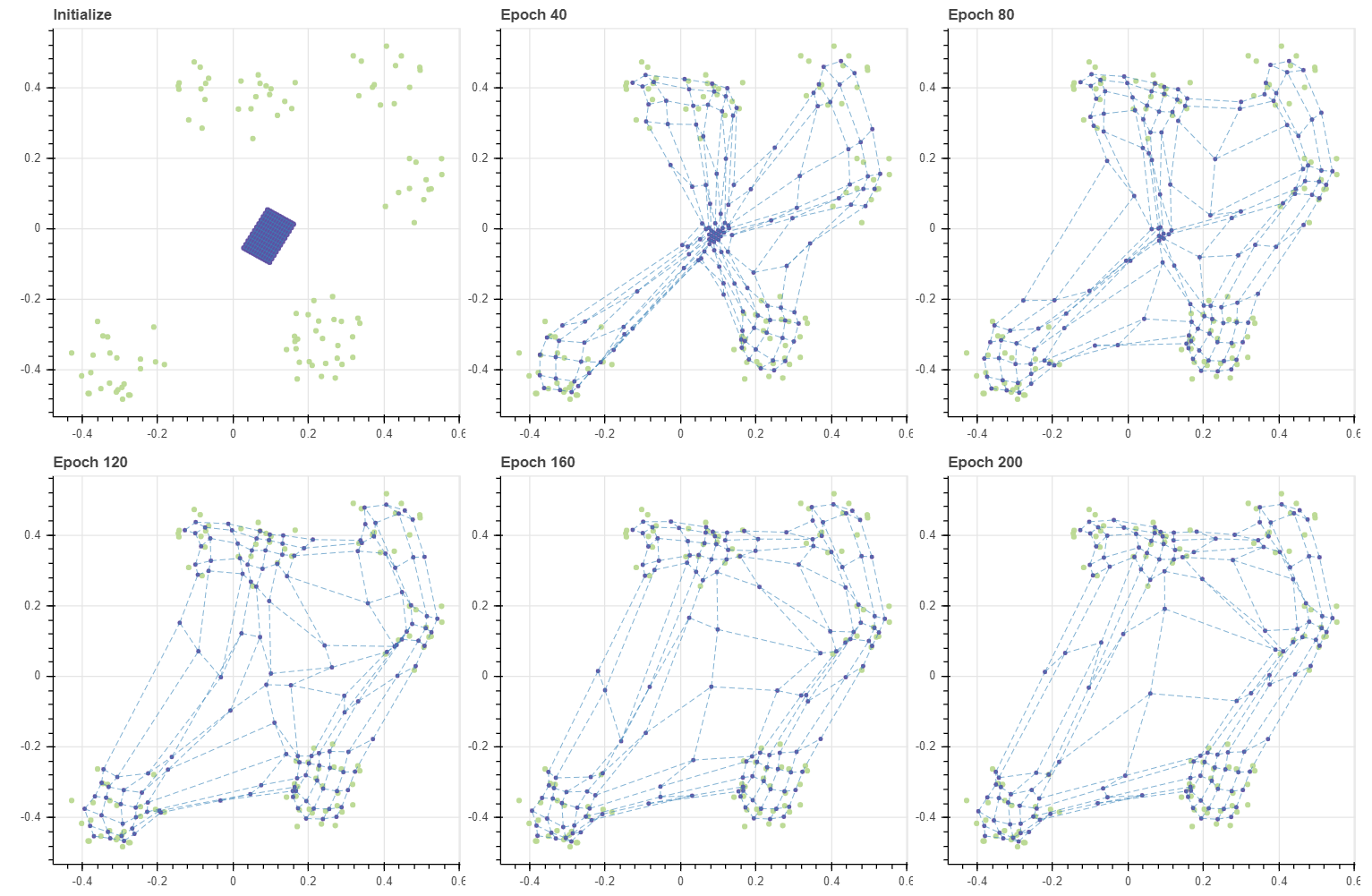
앞서 epochs=20 에 수렴했던 데이터가 이번에는 더 많은 반복을 거쳐야 수렴하였습니다. 더 중요한 점은 학습 패턴입니다. 초기 상태에서 모든 데이터의 BMU 는 그리드의 (5,5) 마디 입니다. 이 마디가 데이터 공간의 (2.0, 2.0) 근처까지 쭉 땅겨지면서 마디 (4,5), (5,4) 를 함께 끌고 갑니다. Epoch 1 에서 BMU 로 세 개의 마디가 선택됨에 따라 (4,4), (3,5), (5,3) 과 같은 마디가 함께 끌려옵니다. 이처럼 마디가 순차적으로 끌려오며 그리드가 전체적으로 이동하는 양상을 보입니다. 그런데 Epoch 20 때에도 (0,0) 마디는 조금밖에 업데이트 되지 않았네요. 즉 그리드를 데이터가 분포하는 공간 근처로 전체적으로 옮기기 위해 수십 번의 epochs 이 필요합니다. 애초에 초기값이 잘 설정되었다면 불필요했을 과정입니다.
그런데 그리드의 크기가 커지면 이 현상은 더 심해집니다. 앞서 BMU 외의 마디들이 학습될 가능성은 그 인접 마디가 BMU 일 때 뿐이었습니다. 그리드의 모서리에 위치한 마디부터 순차적으로 이동하다보니 마디 (0,0) 이 움직일 수 있는 기회는 아주 여러번의 반복이 일어나야 생깁니다. 그런데 그마저도 학습 품질이 좋은 것도 아닙니다. Epoch 1000 의 그림에서 (1.2, 1.0) 부근에 마디들이 모여있음을 볼 수 있습니다. 반대로 (1.4, 2) 나 (1.9, 1.9) 에는 마디들이 거의 없습니다. 데이터의 밀도는 비슷하지만, 모든 마디가 데이터 공간을 훑고 지나가다보니 (1.2, 1.0) 근방의 데이터들이 일종의 장벽이 되어 후반부에 이동한 마디들을 붙잡았습니다. 이후에 그리드를 기반으로 입력데이터의 차원을 2차원으로 변환할 때 이는 공간의 왜곡을 발생시킵니다.
grid, C, pairs = initialize_simple(12, 12)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=1000, masks=masks,
draw_each=[50, 50, 100, 200, 600], epsilon=-0.1, decay=False)
show(gp)
Training time = 1.32 sec; 0.0264/epoch sec
Training time = 1.23 sec; 0.0123/epoch sec
Training time = 2.45 sec; 0.0122/epoch sec
Training time = 4.9 sec; 0.0122/epoch sec
Training time = 14.7 sec; 0.0147/epoch sec
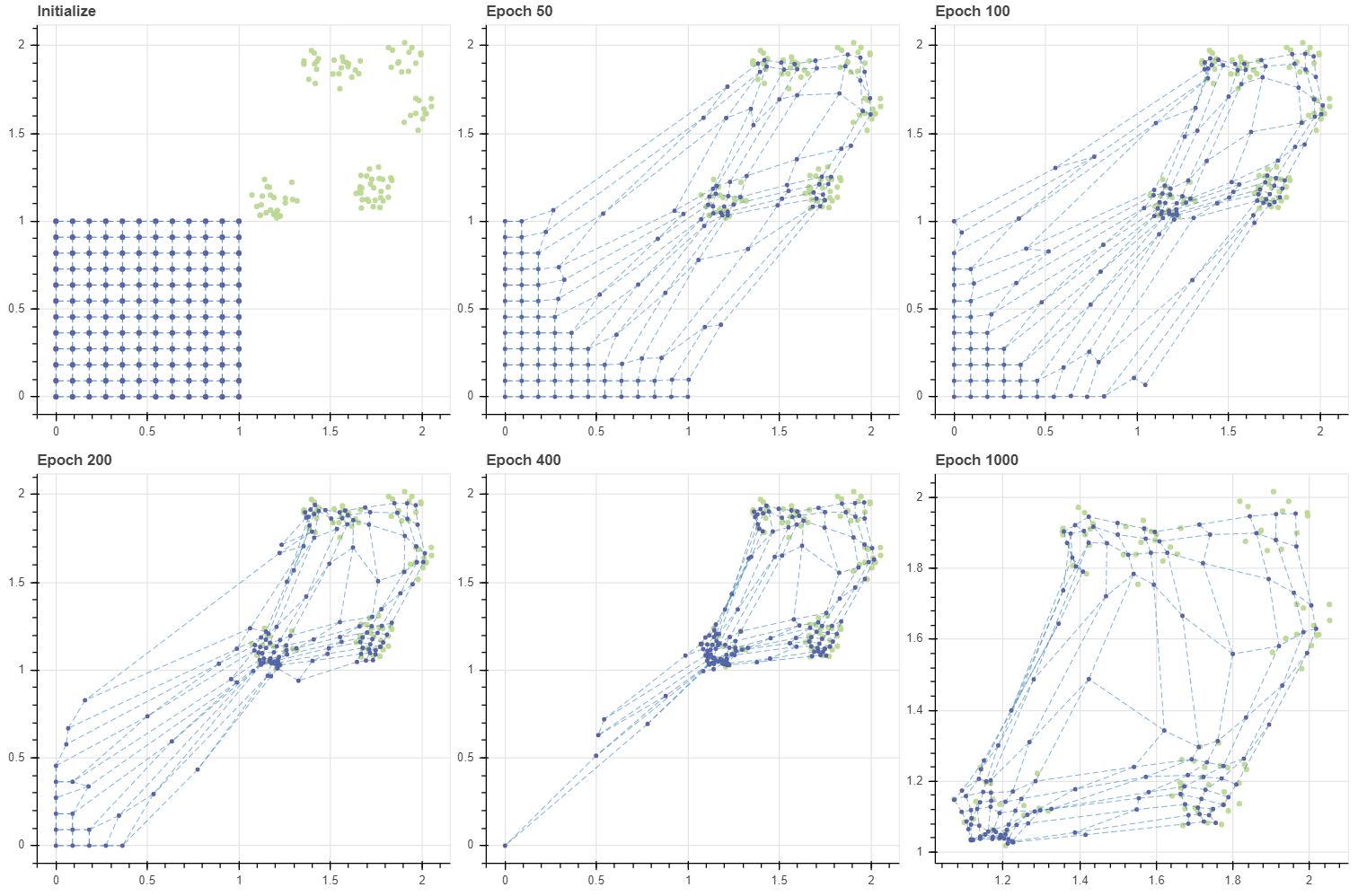
Improving quality of initialization
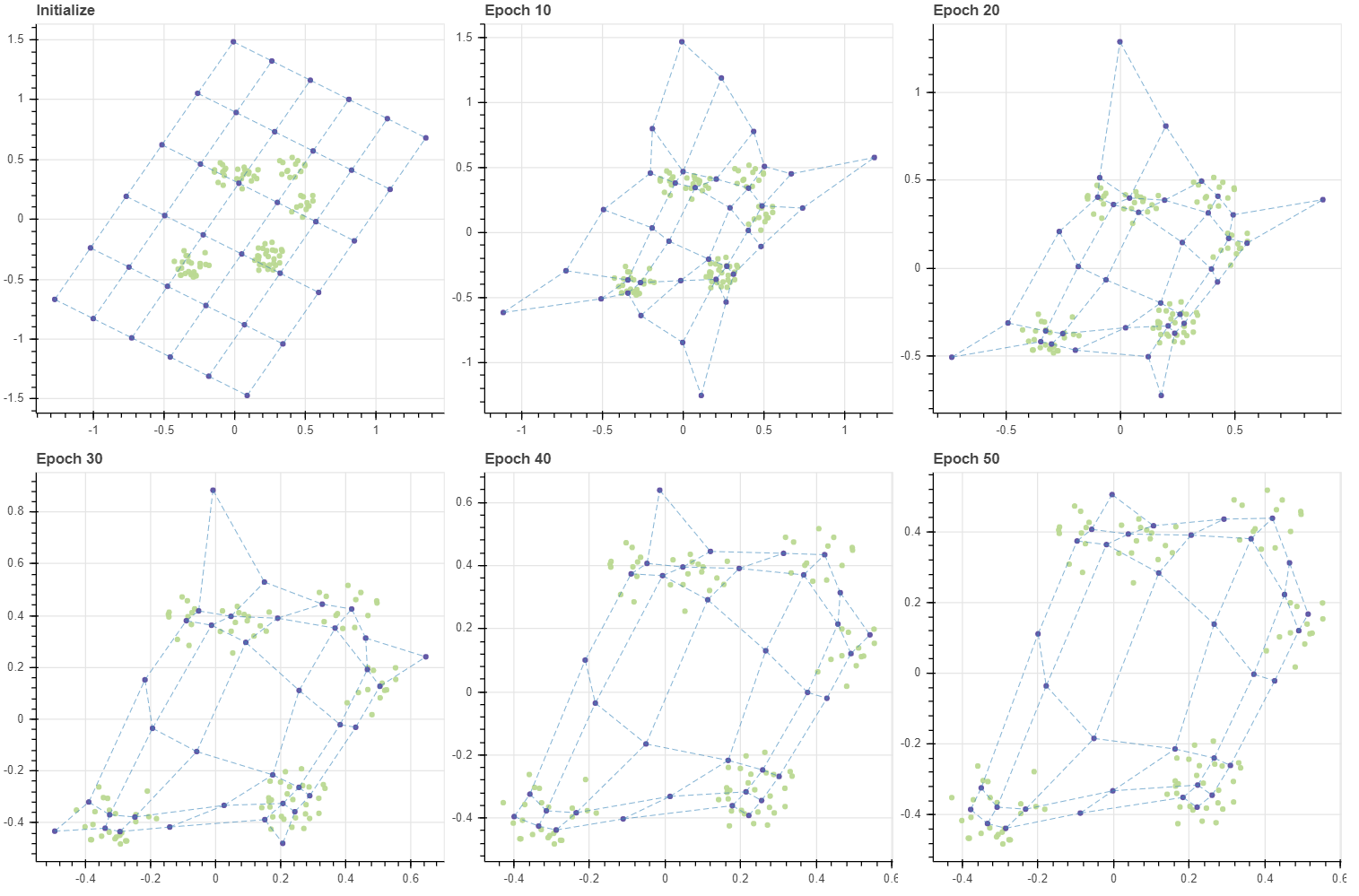
SOM 의 초기화 값으로 일반적으로 0 에 가까운 random vectors 를 이용하라고 자주 말하지만 이는 틀린 주장입니다. 정확히는 데이터로 감싸지는 공간의 중심점의 아주 작은 정렬된 그리드, 혹은 데이터 공간을 감싸는 아주 큰 정렬된 그리드여야 안정적인 학습 성능을 얻을 수 있습니다. 이를 확인하기 위하여 몇 가지 초기화 함수를 구현하였습니다.
method='unitgrid' 는 앞서 이용했던 0 부터 1 사이를 균등하게 나눈 그리드 입니다. 다른 데이터에 대해서도 잘못된 초기값에 따른 성능 저하를 확인하기 위하여 남겨둔 방법입니다.
method='pca' 는 PCA 를 이용하여 데이터를 가장 잘 설명하는 두 개의 축을 학습하고 PC1, PC2 으로 데이터의 2차원 좌표를 표현한 뒤, 이 값의 최대/최소값으로 그리드를 생성하는 것입니다. 여기에 tiny 라는 계수를 함께 이용하는데, tiny=1.0 이면 PC1, PC2 축의 데이터의 최대/최소값으로 그리드를 생성, tiny < 1 이면 데이터 공간의 내부, tiny > 1 이면 데이터를 감싸는 더 큰 그리드를 생성하라는 의미입니다. 개발에 이용하는 데이터는 2차원이기 때문에 PCA 를 적용하면 축회전이 이뤄집니다. 만약 데이터의 차원이 2 보다 크거나 데이터가 sparse matrix 이면 TruncatedSVD 를 이용하였습니다. TruncatedSVD 는 2차원을 2차원으로 변환하는 기능을 제공하지 않습니다.
method='grid' 는 PCA 대신 Random projection 을 이용하여 직교에 가까운 두 개의 축을 임으로 선택한 뒤, 이 축을 PC1 과 PC2 처럼 이용하는 방법입니다. 데이터의 크기가 클 경우 PCA 의 학습에 오랜 시간이 걸릴 수 있습니다. 이때는 ‘random’ 을 이용해도 좋습니다. PCA 와 Random projection 은 기준 축을 학습하는 방법이기 때문에 이들은 coordinate 함수를 공유하도록 구현하였습니다. Random projection 에 대한 설명은 이전의 Locality Sensitive Hashing 설명 포스트를 보시기 바랍니다.
마지막으로 method='random' 은 임의로 마디의 값을 초기화 합니다. tiny 를 이용하여 스캐일을 조절할 수 있도록 하였습니다. 데이터의 평균값을 조절하는 기능은 구현하지 않았습니다. 어자피 실제로는 쓰지 않을, 비교 실험용 함수입니다.
from sklearn.preprocessing import normalize
from sklearn.decomposition import PCA, TruncatedSVD
def initialize(X, n_rows, n_cols, method='grid', tiny=1.0):
grid, pairs = make_grid_and_neighbors(n_rows, n_cols)
# initialize grid using SVD (grid on PC1 and PC2)
if method == 'pca':
C = initialize_pca(n_rows, n_cols, X, tiny)
# initialize grid using Random Projection
elif method == 'grid':
C = initialize_grid(n_rows, n_cols, X, tiny)
# initializes node vectors of 2D grid with equal interval
elif method == 'unitgrid':
C = initialize_unit_grid(n_rows, n_cols,
x_min = kargs.get('x_min', 0),
x_max = kargs.get('x_max', 1),
y_min = kargs.get('y_min', 0),
y_max = kargs.get('y_max', 1))
# initialize node vectors randomly
else:
input_dim = X.shape[1]
C = initialize_random(n_rows * n_cols, input_dim, tiny)
return grid, C, pairs
def initialize_grid(n_rows, n_cols, X, tiny=1.0):
# generate axis 1 randomly
axis1 = np.random.random_sample(X.shape[1]) - 0.5
axis1 /= np.linalg.norm(axis1)
# find orthogonal close axis
axis2 = normalize(np.random.random_sample((10,X.shape[1])) - 0.5, norm='l2')
idx = np.abs(np.inner(axis1, axis2)).argmin()
axis2 = axis2[idx]
# set range
components = np.vstack([axis1, axis2])
z = np.dot(X, components.T)
z = tiny * (z - z.mean(axis=0))
# coordinate
C = coordinate(n_rows, n_cols, axis1, axis2,
x_min = z[:,0].min(), x_max = z[:,0].max(),
y_min = z[:,1].min(), y_max = z[:,1].max(), center = X.mean(axis=0))
return C
def initialize_unit_grid(n_rows, n_cols, x_min=0, x_max=1, y_min=0, y_max=1, center=None, tiny=1.0):
axis = tiny * np.asarray([[1.0, 0.0], [0.0, 1.0]])
return coordinate(n_rows, n_cols, axis[0], axis[1], x_min, x_max, y_min, y_max, center)
def initialize_pca(n_rows, n_cols, X, tiny=1.0):
if tiny == 0:
tiny = 1
# train PCA if input dim == 2
if X.shape[1] == 2:
model = PCA(n_components=2)
# train SVD if input dim > 2 or X is sparse
else:
model = TruncatedSVD(n_components=2)
z = tiny * model.fit_transform(X)
axis = model.components_
C = coordinate(n_rows, n_cols, axis[0], axis[1],
x_min = z[:,0].min(), x_max = z[:,0].max(),
y_min = z[:,1].min(), y_max = z[:,1].max(), center = X.mean(axis=0))
return C
def coordinate(n_rows, n_cols, axis1, axis2, x_min, x_max, y_min, y_max, center=None):
x_values = np.linspace(x_min, x_max, n_rows)
y_values = np.linspace(y_min, y_max, n_cols)
C = [i * axis1 + j * axis2 for i in x_values for j in y_values]
C = np.asarray(C)
if center is not None:
C = C + center
return C
def initialize_random(n_codes, input_dim, tiny=1.0):
return tiny * (np.random.random_sample((n_codes, input_dim)) - 0.5)
구현된 초기화 방법을 이용하여 앞선 데이터를 (12,12) 그리드로 재학습합니다. Random projection 에 기반한 초기화 방법을 이용하였습니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
X += 1.0
grid, C, pairs = initialize(X, 12, 12, method='grid', tiny=1.0)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=200, masks=masks, draw_each=40, epsilon=-0.1, decay=False)
show(gp)
Training time = 1.09 sec; 0.0272/epoch sec
Training time = 0.996 sec; 0.0124/epoch sec
Training time = 0.996 sec; 0.0083/epoch sec
Training time = 1.0 sec; 0.00625/epoch sec
Training time = 1.0 sec; 0.005/epoch sec
초기화 상태에서 정확히 데이터를 감싸는 대각선 방향의 그리드가 만들어졌습니다. 그리고 데이터와 가까운 마디부터 우선적으로 데이터에 달라붙고 주변 마디들이 천천히 다가옵니다. 이는 앞서 살펴보았던 안정적인 SOM 학습과 비슷한 패턴입니다. 각 클러스터 마다 달라붙은 마디의 개수도 대체로 균등해 보입니다.
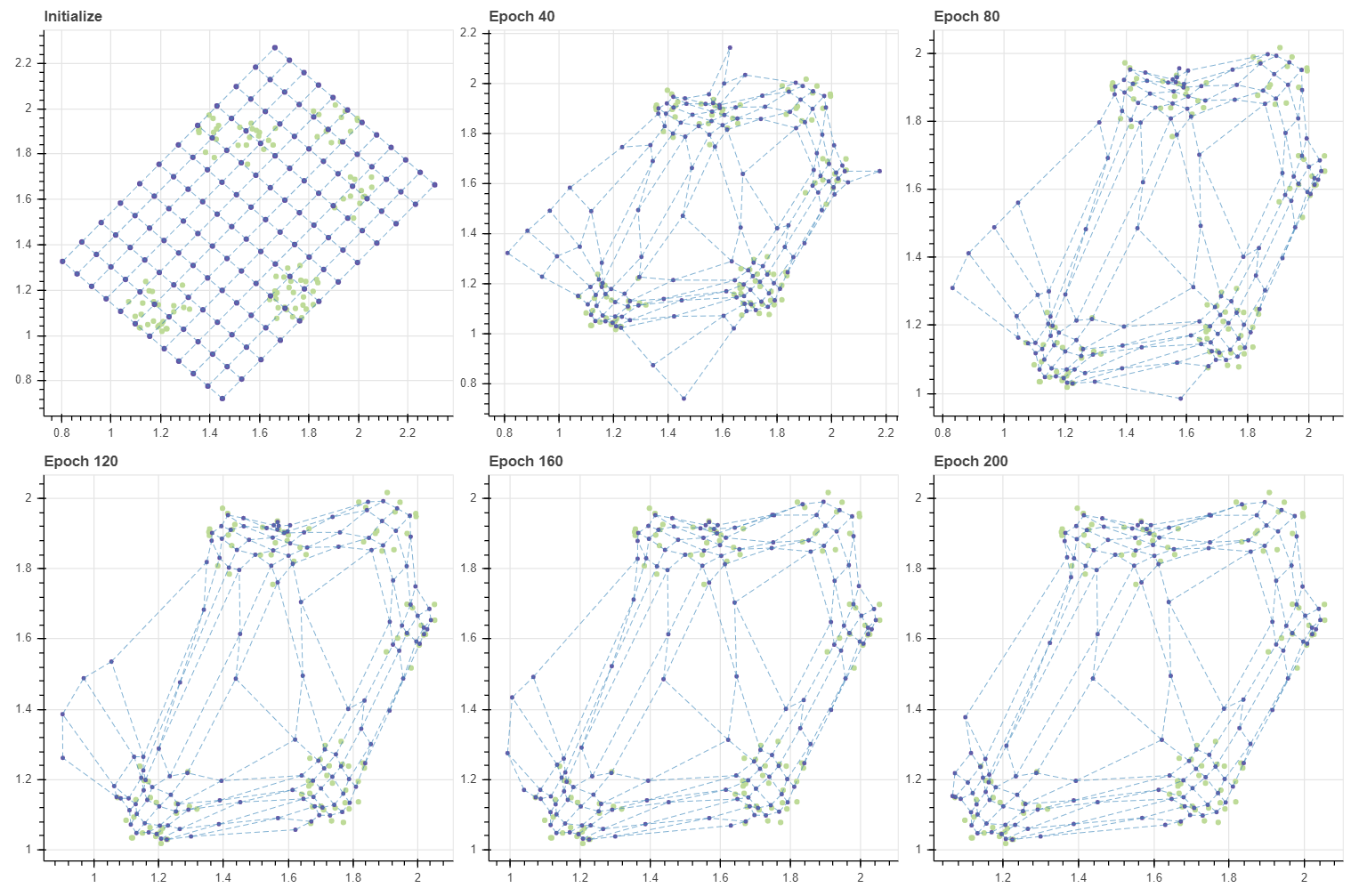
이번에는 그리드의 크기를 작게 만들어 데이터로 감싸지는 공간의 중심에 그리드를 만들었습니다. Random projection 을 이용하다보니 그리드의 방향이 조금 달라졌습니다.
grid, C, pairs = initialize(X, 12, 12, method='grid', tiny=0.1)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=200, masks=masks, draw_each=40, epsilon=-0.1, decay=False)
show(gp)
Training time = 1.08 sec; 0.027/epoch sec
Training time = 0.987 sec; 0.0123/epoch sec
Training time = 0.983 sec; 0.00819/epoch sec
Training time = 0.988 sec; 0.00617/epoch sec
Training time = 0.984 sec; 0.00492/epoch sec
이번에는 그리드의 바깥 부분의 마디들이 데이터에 우선적으로 달라붙고 그 뒤 순차적으로 그리드의 중심에 위치한 마디들이 순차적으로 이동합니다. 클러스터 별 마디의 분포도 대체로 균등해보입니다만, 그리드가 삐뚤어져 보이긴합니다.
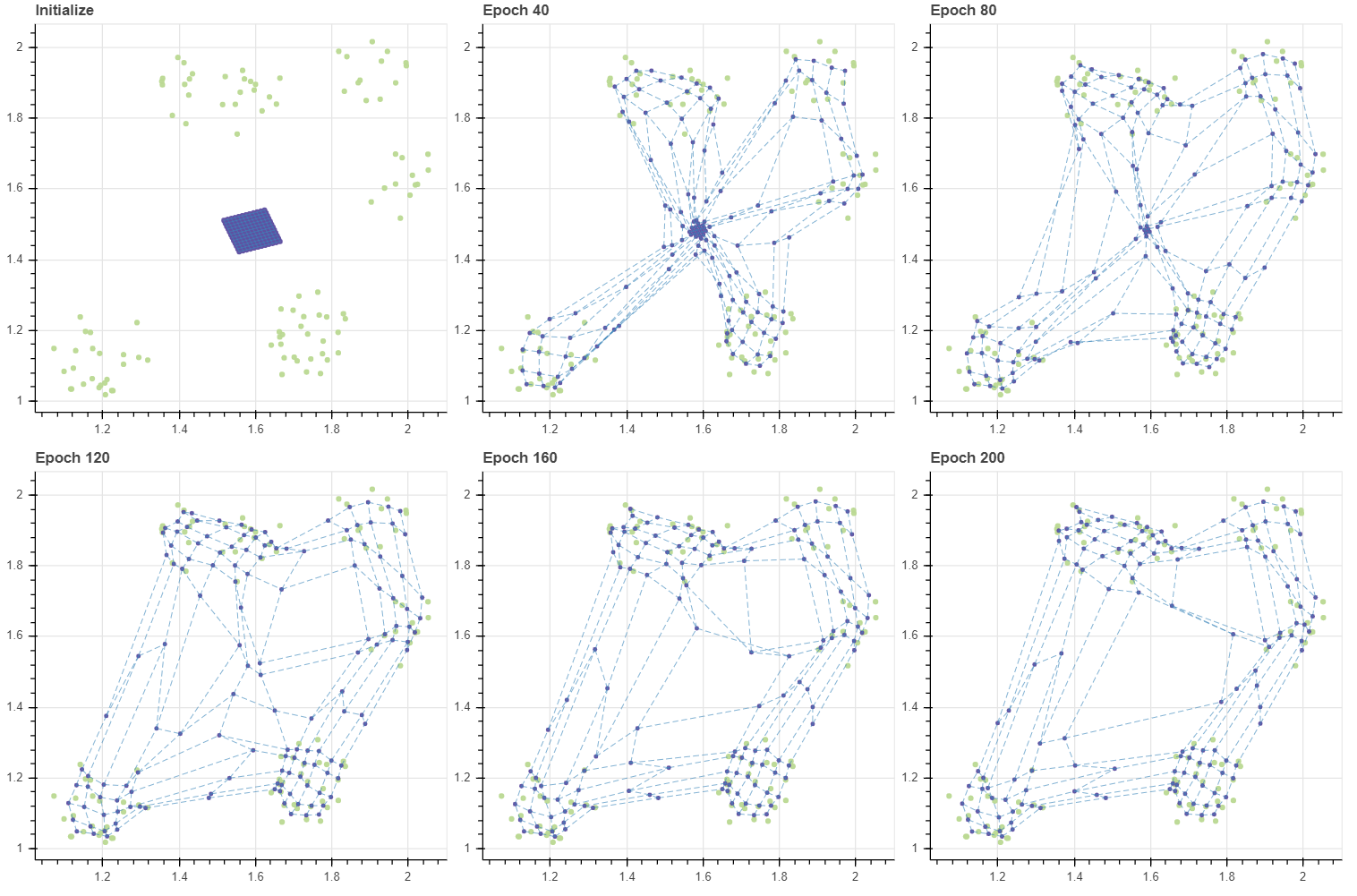
이번에는 tiny=3.0 으로 설정하여 데이터보다 훨씬 큰 그리드로 초기화를 한 뒤 SOM 을 학습합니다. 이때는 그리드의 중간에 위치한 마디들이 우선적으로 데이터에 달라붙고 가장자리의 마디들이 천천히 달라붙습니다. 그리드의 중심이 데이터의 중심과 대체로 일치하면 tiny 의 값과 상관없이 어느 정도 안정적인 성능을 보여줍니다.
grid, C, pairs = initialize(X, 12, 12, method='grid', tiny=3.0)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=300, masks=masks, draw_each=60, epsilon=-0.1, decay=False)
show(gp)
Training time = 1.57 sec; 0.0262/epoch sec
Training time = 1.48 sec; 0.0123/epoch sec
Training time = 1.49 sec; 0.00826/epoch sec
Training time = 1.48 sec; 0.00617/epoch sec
Training time = 1.48 sec; 0.00493/epoch sec
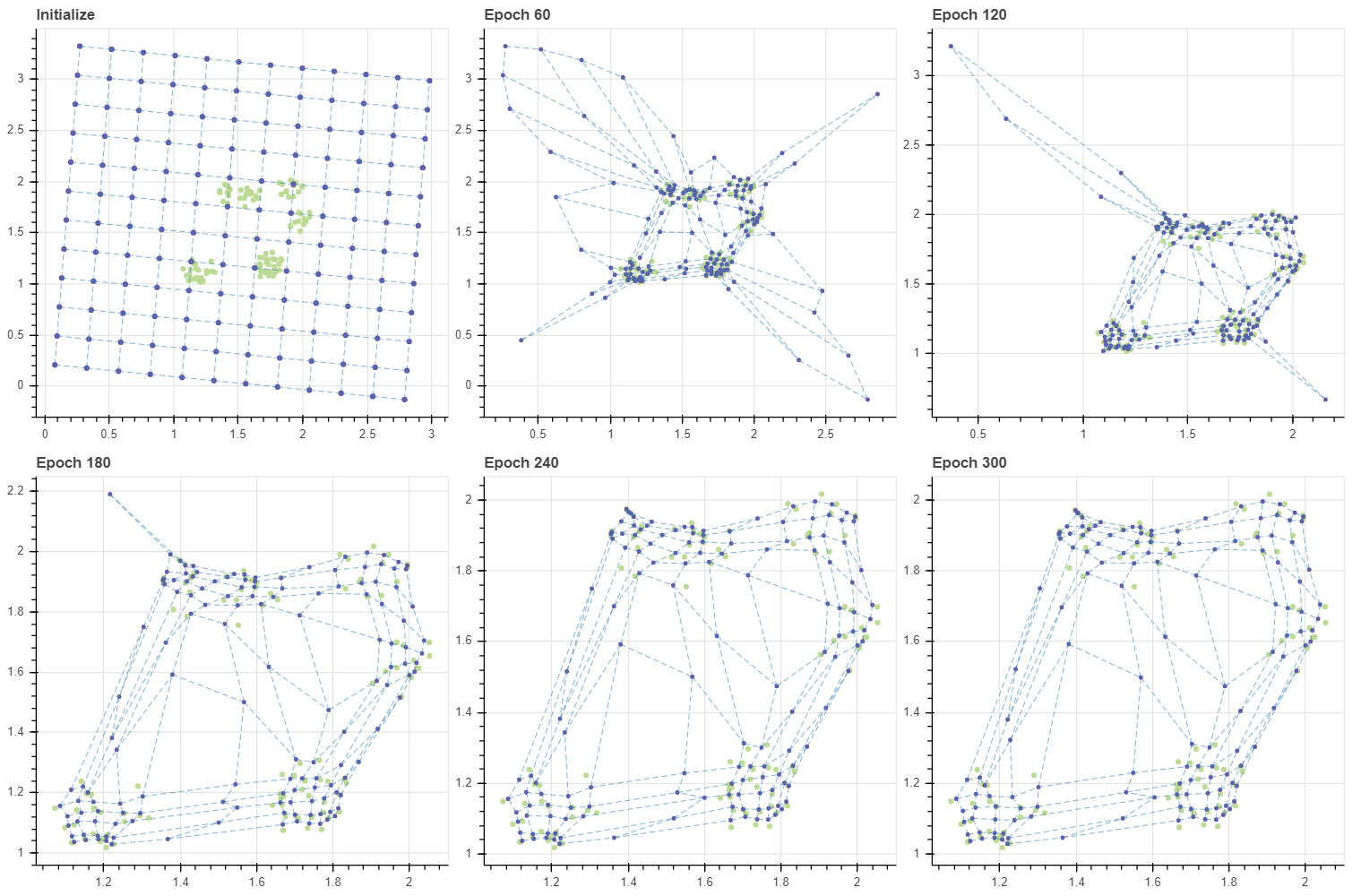
하지만 그리드를 랜덤 벡터로 초기화하면 그리드 공간이 꼬입니다. Epoch 500 에서는 그리드 내 인접한 마디가 실제로 학습 데이터의 인접한 공간을 대표하지 않을 가능성이 있습니다. 공간을 가로지르는 연결선들이 다수 존재하기 때문입니다. 물론 꼬인 그리드가 몇 천번의 반복 학습을 수행하면 풀리긴 합니다만, 애초에 랜덤 벡터를 이용하지 않으면 될 문제입니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
X -= 0.5
grid, C, pairs = initialize(X, 12, 12, method='random', tiny=0.1)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=500, masks=masks, draw_each=100, epsilon=-0.1, decay=False)
show(gp)
Training time = 2.53 sec; 0.0253/epoch sec
Training time = 2.45 sec; 0.0123/epoch sec
Training time = 2.44 sec; 0.00813/epoch sec
Training time = 2.44 sec; 0.0061/epoch sec
Training time = 2.44 sec; 0.00488/epoch sec
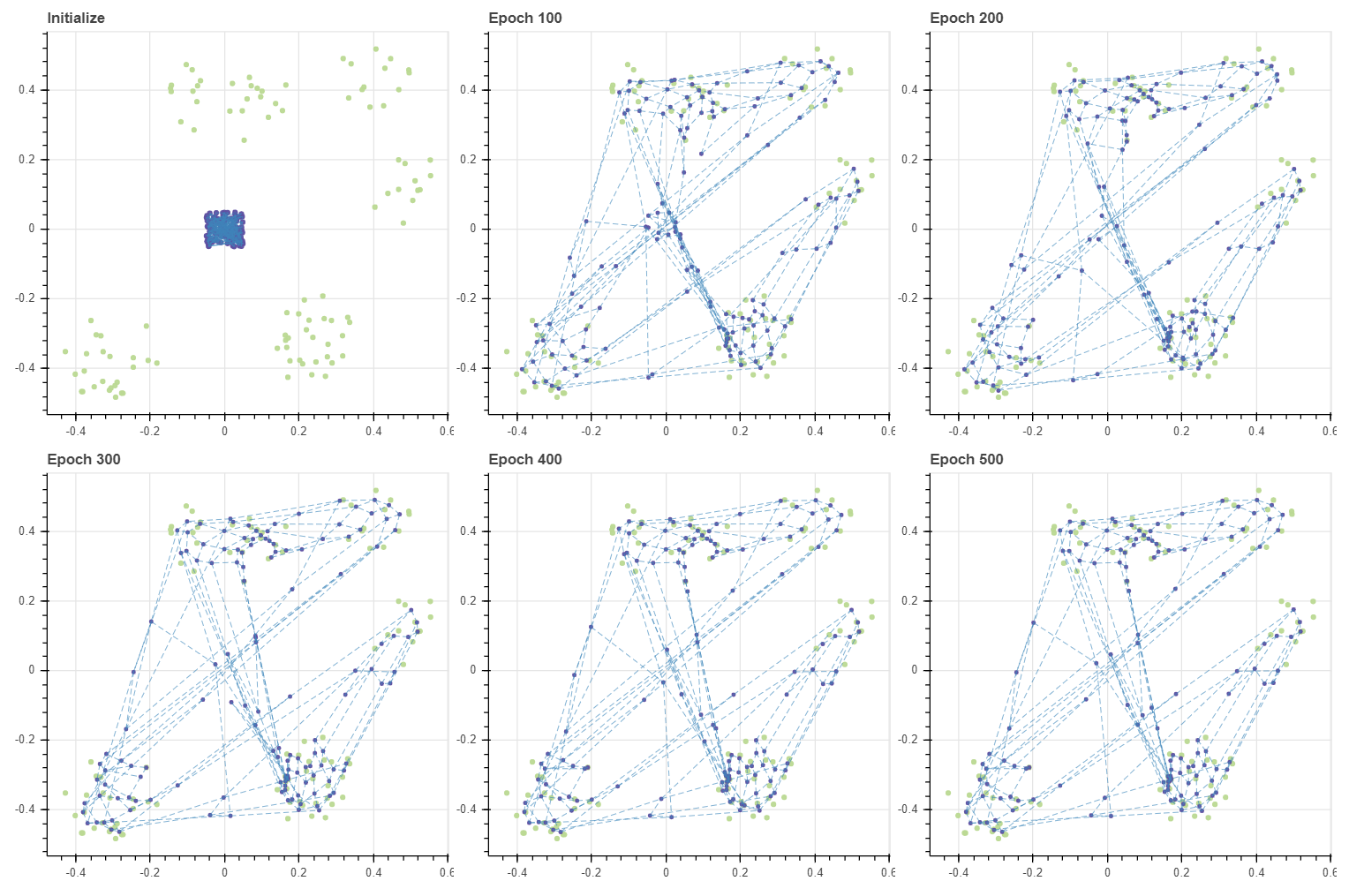
PCA 를 이용하여 학습할 경우에도 약 epoch 200 에 가까워지니 어느 정도 안정적인 그리드가 학습됩니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
X -= 0.5
grid, C, pairs = initialize(X, 12, 12, method='pca', tiny=0.1)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=200, masks=masks, draw_each=40, epsilon=-0.1, decay=False)
show(gp)
정리하면 초기값은 데이터로 감싸지는 중심부에서 정렬된 작은 그리드나 데이터를 감쌀 수 있는 큰 그리드를 초기값으로 이용하는 것이며, 원점 근처의 작은 값들로 그리드를 초기화 하더라도 데이터 분포와 크게 어긋날 경우 그리드가 전체적으로 이동하는 과정에서 불필요한 학습이 이뤄지고, 그리드와 데이터가 처음 만나는 부분의 데이터에 마디들이 걸려 불균형적으로 마디가 분포할 수 있습니다.
Mini-batch style
그런데 왜 SOM 은 stochastic gradient descent 방식으로 학습할까요? 이것은 논문에서 찾은 내용이 아닌, 사견입니다. SOM 은 1980 년대에 제안된 모델이고 당시에는 큰 데이터를 실험에 자주 이용하지 않았습니다 (실험이 끝나긴 해야죠). 적은 수의 데이터를 이용하여 모델을 학습하기 위해서 학습 데이터 하나마다 업데이트를 시켰다고 생각합니다. 사실 학습데이터를 임의의 순서로 뒤섞은 뒤 매우 작은 learning rate 로 stochastic gradient descent 를 이용하면 minibatch style 로 학습하는 것과 성능이 크게 다르지는 않습니다. 이번에는 minibatch style 로 update 하는 함수를 만든 뒤, 앞서 만든 fit 과 함께 이용합니다.
to_minibatch 는 numpy.ndarray 나 scipy.sparse.csr_matrix 형태의 데이터가 입력되었을 때 이를 여러 개의 mini-batch 로 나누는 함수입니다. 만약 batch_size 가 0 보다 작다면 batch style 로 학습하는 것이므로 입력데이터를 그대로 yield 합니다. 그렇지 않다면 데이터의 rows 를 임의의 순서로 섞은 뒤 slice 를 하여 yield 를 합니다. Minibatch 는 batch style 함수에 sliced matrix 를 각각 입력하면 됩니다. 그러므로 update_batch 를 먼저 구현합니다. 이 함수는 미리 gradient 를 저장할 grad 라는 행렬을 만든 뒤, 앞서 stochastic gradient descent 와 같은 방식으로 Xi - C 에 기반한 gradient 를 계산합니다. 이에 마스크를 적용한 값을 grad 에 누적합니다. 그 뒤 모든 Xi 의 gradient 의 평균을 C 에 더해줍니다.
def update_minibatch(X, C, lr=0.01, metric='euclidean', batch_size=4, masks=None, **kargs):
n_data = X.shape[0]
n_codes, n_features = C.shape
C_new = C.copy()
for b, Xb in enumerate(to_minibatch(X, batch_size)):
C_new = update_batch(Xb, C_new, lr, metric, masks)
return C_new
def to_minibatch(X, batch_size):
if batch_size <= 0:
yield X
n_data = X.shape[0]
n_batches = math.ceil(n_data / batch_size)
indices = np.random.permutation(n_data)
for batch in range(n_batches):
b = batch * batch_size
e = (batch + 1) * batch_size
yield X[b:e]
def update_batch(X, C, lr=0.01, metric='euclidean', masks=None, **kargs):
n_data = X.shape[0]
n_codes, n_features = C.shape
C_new = C.copy()
grad = np.zeros(C.shape, dtype=C.dtype)
for i, Xi in enumerate(X):
bmu, _ = closest(Xi.reshape(1,-1), C, metric)
bmu = int(bmu) # matrix shape=(0,)
diff = Xi - C # shape = (n_codes, n_features)
grad_i = lr * diff * masks[bmu][:,np.newaxis]
grad += grad_i
C_new += grad / n_data
return C_new
minibatch stype 로 만든 함수를 이용하기 위해 keyword argument 에 update_func 로 update_minibatch 함수를 입력합니다. 이를 위해서 앞서 fit 함수에 **kargs 를 준비해 뒀었습니다. 구현한 함수가 제대로 작동하는지 오랜만에 (6,6) 크기의 작은 그리드를 만들어 학습 결과를 확인합니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
X -= 0.5
grid, C, pairs = initialize(X, 6, 6, method='pca', tiny=2.0)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=50, masks=masks, draw_each=10,
epsilon=-0.1, decay=False, update_func=update_minibatch)
show(gp)
Training time = 0.296 sec; 0.0296/epoch sec
Training time = 0.29 sec; 0.0145/epoch sec
Training time = 0.267 sec; 0.00888/epoch sec
Training time = 0.249 sec; 0.00623/epoch sec
Training time = 0.245 sec; 0.00489/epoch sec
c-means style update
안정적인 초기화 값을 얻는 방법은 알았습니다. 그러나 앞서 안정적인 방법으로 초기화를 하더라도 (12,12) 크기의 그리드가 학습되는데 약 300 epochs 가 필요하였습니다. 전체 학습시간은 약 7.5 초 였습니다. 겨우 100 여개의 데이터를 학습하는 비용치고는 매우 비쌉니다. 이후에 수십만개의 데이터를 거대한 그리드에 매핑하려면 하루가 넘게 걸리지도 모릅니다. 이번에는 학습 속도를 개선해봅니다.
Mini-batch style 로 학습하는 함수를 만들었지만, gradient 를 누적하다가 한 번에 업데이트 할 뿐, gradient 의 계산 횟수는 크게 줄지 않았습니다. 그 이유 중 하나는 마스크를 이용하는 방식으로 구현하였기 때문입니다. 모든 마디에 대하여 \(W_v - X_i\) 를 계산한 뒤, 사용하지 않을 gradient 에 0 을 곱하면 결국 마디의 개수가 늘어날 때 그에 비례하여 gradient 의 계산 횟수가 늘어난다는 의미이기 때문입니다. 어자피 0 이 곱해질 부분은 애초에 계산을 하지 말아야 합니다.
또한 학습이 안정된 SOM 의 경우 마디가 이동하는 방향이 어디인지도 고민할 필요가 있습니다. SOM 의 한 마디는 그 마디를 BMU 로 지니는 학습데이터의 평균 근처로 이동합니다. 물론 그 이웃 마디를 BMU 로 지니는 다른 학습데이터의 영향도 받습니다. 이를 고려하면 SOM 의 한 마디는 BMU 와의 거리가 얼마인지에 따라 차등된 가중치가 곱해진 가중 평균 근처로 이동합니다. 그렇다면 BMU 와 BMU 의 이웃한 마디에 해당하는 데이터들에 대하여 가중 평균을 계산하면 됩니다. 만약 이웃한 마디를 고려하지 않는다면 이는 k-means 의 학습 방식입니다. 그런데 \(X_i\) 가 가장 가까운 하나의 마디 뿐 아니라 그리드 상에서 가까운 몇 개의 마디들을 한꺼번에 업데이트 하기 때문에 이는 fuzzy k-means 인 c-means 와 매우 유사합니다. 앞으로 이를 c-means style 이라 명하겠습니다.
이를 위하여 그리드의 이웃 구조를 표현하는 새로운 인덱스를 만듭니다. make_neighbor_graph 는 grid 가 입력되면 한 마디와 Manhattan distance 가 max_width 를 넘지 않는 마디에 대하여 그 거리의 승수만큼 decay 를 곱한 값을 가중치로 부여합니다. 그리고 역이웃 인덱스 (inverse neighbor graph) 도 함께 만듭니다. 이는 이후에 다른 기능의 구현에서 필요합니다.
def make_neighbor_graph(grid, max_width=2, decay=0.25):
def weight_array(f, s):
return np.asarray([np.power(f,i) for i in range(1, s+1) for _ in range(4*i)])
def pertubate(s):
def unique(i, s):
if abs(i) == s:
return [0]
return [s - abs(i), -s + abs(i)]
def pertubate_(s_):
return [(i,j) for i in range(-s_, s_+1) for j in unique(i, s_)]
return [pair for s_ in range(1, s+1) for pair in pertubate_(s_)]
def is_outbound(i_, j_):
return (i_ < 0) or (i_ >= n_rows) or (j_ < 0) or (j_ >= n_cols)
n_rows, n_cols = grid.shape
n_codes = n_rows * n_cols
W = weight_array(decay, max_width)
N = -np.ones((n_codes, W.shape[0]), dtype=np.int)
N_inv = -np.ones((n_codes, W.shape[0]), dtype=np.int)
for row, (i, j) in enumerate(zip(*np.where(grid >= 0))):
idx_b = grid[i,j]
for col, (ip, jp) in enumerate(pertubate(max_width)):
if is_outbound(i+ip, j+jp):
continue
idx_n = grid[i+ip, j+jp]
N[idx_b,col] = idx_n
N_inv[idx_n,col] = idx_b
return N, N_inv, W
아래와 같은 (4,4) 크기의 그리드의 경우에 좌/우/상/하에 위치한 이웃을 N 행렬로 표현합니다. 예를 들어 N[0] 은 그리드의 0 번 마디이며, 오른쪽에 1 번, 아래쪽에 4 번 마디가 위치한다는 의미입니다. 왼쪽과 위쪽에는 마디가 없으므로 -1 을 부여합니다.
grid = np.asarray(
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]]
)
N, N_inv, W = make_neighbor_graph(grid, max_width=1)
N
array([[-1, 1, -1, 4],
[-1, 2, 0, 5],
[-1, 3, 1, 6],
[-1, -1, 2, 7],
[ 0, 5, -1, 8],
[ 1, 6, 4, 9],
[ 2, 7, 5, 10],
[ 3, -1, 6, 11],
[ 4, 9, -1, 12],
[ 5, 10, 8, 13],
[ 6, 11, 9, 14],
[ 7, -1, 10, 15],
[ 8, 13, -1, -1],
[ 9, 14, 12, -1],
[10, 15, 13, -1],
[11, -1, 14, -1]])
이 방법 역시 minibatch style 로 구현할 수 있습니다. update_cmeans 는 mini-batch style 을 이용할 수 있도록 준비합니다. batch_size > 1 이라면 to_minibatch 함수를 이용하여 입력데이터를 slice 하여 각각을 이용하여 C 를 업데이트 합니다. 그렇지 않다면 udpate_cmeans_batch 함수를 이용하여 c-means 처럼 학습합니다. C_cont 는 C 에 업데이트 될 새로운 content 입니다. BMU 에 해당하는 학습데이터들은 그대로 C_cont 에 더하고, 이웃한 마디가 BMU 일 경우에는 그에 해당하는 가중치만큼을 곱하여 C_cont 에 더합니다. 그 뒤 더해진 가중치의 총합으로 나눕니다. 이 값을 이전 시점의 C 와 update_ratio : 1 - update_ratio 비율로 혼합합니다. 만약 update_ratio=1 이라면 이전 시점의 값은 전혀 이용하지 않고 c-means 처럼 학습한다는 의미입니다. 다른 arugment 인 adjust_ratio 는 이후에 설명하겠습니다.
def update_cmeans(X, C, update_ratio, metric='euclidean', batch_size=-1,
grid=None, neighbors=None, inv_neighbors=None, weights=None,
adjust_ratio=0.5, max_width=2, decay=0.25, **kargs):
if (neighbors is None) or (weights is None):
neighbors, inv_neighbors, weights = make_neighbor_graph(grid, max_width, decay)
C_new = C.copy()
for b, Xb in enumerate(to_minibatch(X, batch_size)):
C_new = update_cmeans_batch(Xb, C_new, update_ratio, metric,
neighbors, inv_neighbors, weights, adjust_ratio)
return C_new
def update_cmeans_batch(X, C, update_ratio, metric, neighbors, inv_neighbors, weights, adjust_ratio):
n_data = X.shape[0]
n_codes = C.shape[0]
C_cont = np.zeros(shape=C.shape)
W_new = np.zeros(n_codes)
bmu, dist = closest(X, C, metric)
for bmu_c in range(n_codes):
# find instances corresponding BMU
indices = np.where(bmu == bmu_c)[0]
n_matched = indices.shape[0]
if n_matched == 0:
continue
Xc = np.asarray(X[indices,:].sum(axis=0)).reshape(-1)
C_cont[bmu_c] += Xc
W_new[bmu_c] += n_matched
# equivalent to kmeans (no regard to neighbors)
if weights.shape[0] == 0:
continue
# update sum of vectors neighbors of BMU
for c, w in zip(neighbors[bmu_c], weights):
if c == -1:
continue
C_cont[c] += w * Xc
W_new[c] += w * n_matched
C_new = update_ratio * C_cont + (1 - update_ratio) * C
return C_new
앞서 만든 update_cmeans 함수를 이용하여 SOM 을 학습합니다. 이 함수는 grid 를 이용하기 때문에 keyword arguments 로 grid 를 입력합니다. 그리고 실험을 위해 adjust_ratio=0 으로 설정합니다. learning rate lr 은 position argument 이기 때문에 fit 함수의 lr 은 update_cmeans 의 update_ratio 로 이용됩니다. lr=1.0 = update_ratio=1.0 이므로 c-means style 로 그리드를 학습합니다. 극적인 확인을 위하여 이번에는 그리드의 크기를 (20,20) 으로 키웠습니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
X -= 0.5
grid, C, pairs = initialize(X, 20, 20, method='grid', tiny=0.1)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=50, draw_each=[5, 5, 10, 10, 20], epsilon=-0.1,
decay=False, update_func=update_cmeans, lr=1.0, grid=grid, adjust_ratio=0)
show(gp)
Training time = 0.0762 sec; 0.0152/epoch sec
Training time = 0.0875 sec; 0.00875/epoch sec
Training time = 0.179 sec; 0.00895/epoch sec
Training time = 0.181 sec; 0.00602/epoch sec
Training time = 0.361 sec; 0.00723/epoch sec
그런데 그 결과 특이한 현상이 발생합니다. 대부분의 마디들은 데이터에 달라붙는데 (0.0, 0.0) 근방에 여러 개의 마디들이 남아있습니다. 이는 BMU 혹은 그 인접한 마디들로도 선택되지 않는 마디들입니다. C_cont 가 zero vector 이기 때문에 c-means style 로 학습하면 이러한 마디는 영원히 학습이 이뤄지지 않습니다. 그리드의 크기가 데이터의 개수에 비하여 매우 크기 때문에 발생하는 문제입니다. 물론 마디의 개수를 크게 줄이면 이러한 문제가 발생할 가능성이 줄어듭니다 (발생하지 않는다고 보장할 수는 없습니다). 그리드를 계속하여 키워 학습하는 이유는 이들이 빈 공간을 세밀하게 학습할 수 있기 때문입니다. 이 문제를 해결해 봅시다.
이 문제가 발생한 이유는 어떤 마디는 BMU 혹은 BMU 주위의 마디보다도 훨씬 멀기 때문입니다. 하나의 학습데이터 포인트 \(X_i\) 가 영향을 줄 수 있는 마디는 BMU 의 이웃의 이웃 정도입니다. 물론 max_width 를 크게 키울 수도 있겠지만, 그만큼 업데이트 되는 마디의 개수가 늘어나게 됩니다. 또한 멀리 떨어진 마디는 가중치가 작아 업데이트의 속도도 느릴 것입니다. 이를 해결하기 위하여 몇 가지 트릭을 이용하였습니다. 마디가 업데이트 될 때의 가중치의 합이 W_new 에 누적되고 있었습니다. 첫번째 트릭으로 이 값이 0 인 마디들은 일단 이전 시점의 C 를 C_cont 로 이용합니다. 업데이트가 되지 않으면 이전 시점에서 움직이지 말라는 의미입니다. 두번째로 가중치 합이 0 인 마디들은 자신의 이웃 마디의 가중 평균으로 이동하는 것입니다. 만약 자신 주변 이웃들 역시 한번도 움직이지 않는다면 그 마디는 영원히 움직이지 않습니다. 그러나 그럴 일은 없음을 보장할 수 있습니다.
만약 \(X_i\) 의 BMU 가 a 이고 이는 a-b-c 로 연결, c 는 c-d-e 로 연결되었다고 가정합니다. BMU 의 이웃인 c 는 오로직 \(X_i\) 에 의해서만 업데이트가 이뤄졌습니다. 그리고 d 와 e 는 학습 과정 내내 어떤 데이터의 BMU 혹은 이웃 마디로도 선택되지 않았다고 가정하더라도 d 의 이웃인 c 가 이동했기 때문에 d 의 이웃의 가중 평균을 이용하면 C_cont[d] 는 C[d] 와 다른 값을 가집니다. 이번에 d 가 이동하였다면 다음 반복 과정에서는 d 에 이웃한 e 가 그 값을 이용하게 됩니다. 즉 학습데이터에 의하여 업데이트가 되지 않은 마디는 스스로 업데이트 된 마디를 쫓아가게 함으로써 모든 마디가 업데이트가 이뤄집니다. 그리고 이웃의 가중 평균으로 새로운 C_cont 를 만드는 비중을 adjust_ratio 로 조절합니다.
def update_cmeans_batch(X, C, update_ratio, metric, neighbors, inv_neighbors, weights, adjust_ratio):
for bmu_c in range(n_codes):
# do something
# ...
nonzero_indices = np.where(W_new > 0)[0]
inverse_norm = np.zeros(n_codes)
inverse_norm[nonzero_indices] = W_new[nonzero_indices] ** -1
C_cont = C_cont * inverse_norm[:,np.newaxis]
# stuck nodes move around to the their updated neighbors by themselves
if adjust_ratio > 0:
stuck_indices = np.where(W_new == 0)[0]
stuck_mask = np.ones(n_codes)
stuck_mask[np.where(W_new > 0)[0]] = 0
W_stuck = np.zeros(n_codes)
C_stuck = np.zeros(C.shape)
C_cont[stuck_indices] = C[stuck_indices]
w_0 = weights[0]
for j, w in enumerate(weights):
w = min(0.95, adjust_ratio) * w / w_0
contents = np.zeros(C.shape)
rows = np.where(inv_neighbors[:,j] >= 0)[0]
contents[rows] = w * C_cont[inv_neighbors[rows,j]]
contents = contents * stuck_mask[:,np.newaxis]
W_stuck[rows] += w
C_stuck += contents
nonzero_indices = np.where(W_stuck > 0)[0]
inverse_norm = np.zeros(n_codes)
inverse_norm[nonzero_indices] = W_stuck[nonzero_indices] ** -1
C_stuck = C_stuck * inverse_norm[:,np.newaxis]
C_cont[stuck_indices] = C_stuck[stuck_indices]
C_new = update_ratio * C_cont + (1 - update_ratio) * C
return C_new
이 방법을 포함하는 새로운 update_cmeans 방법을 이용하여 (20, 20) 크기의 그리드를 동일한 데이터로 학습합니다.
grid, C, pairs = initialize(X, 20, 20, method='grid', tiny=0.1)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=50, draw_each=[5, 5, 10, 10, 20], epsilon=-0.1,
decay=False, update_func=update_cmeans, lr=0.5, grid=grid, adjust_ratio=0.5)
show(gp)
Training time = 0.0724 sec; 0.0145/epoch sec
Training time = 0.08 sec; 0.008/epoch sec
Training time = 0.173 sec; 0.00863/epoch sec
Training time = 0.176 sec; 0.00587/epoch sec
Training time = 0.357 sec; 0.00714/epoch sec
Epoch 5 까지는 데이터와 가까운 마디들이 빠르게 데이터에 달라붙었습니다. Epoch 10 까지도 (0.0, 0.0) 주변에 많은 마디가 위치합니다만, Epoch 20 이후부터는 이들이 점점 데이터에 안정적으로 붙어있는 마디들 근처로 이동합니다. 결국 Epoch 50 에는 그리드가 안정적으로 펼쳐졌습니다. 그런데 이전에 PCA 를 이용한 경우에 (12, 12) 크기의 그리드가 Epoch 200 정도에 안정적으로 학습되었습니다. 이와 비교하면 훨씬 큰 크기의 그리드가 더 적은 반복 횟수만으로도 더 안정적으로 학습된 것입니다.
이번에는 초기값을 데이터보다 더 큰 그리드로 만들었습니다. 이때도 약 50 번의 epochs 만으로도 학습이 수렴함을 확인할 수 있습니다.
grid, C, pairs = initialize(X, 20, 20, method='grid', tiny=2.0)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=50, draw_each=[5, 5, 10, 10, 20], epsilon=-0.1,
decay=False, update_func=update_cmeans, lr=0.5, grid=grid, adjust_ratio=0.5)
show(gp)
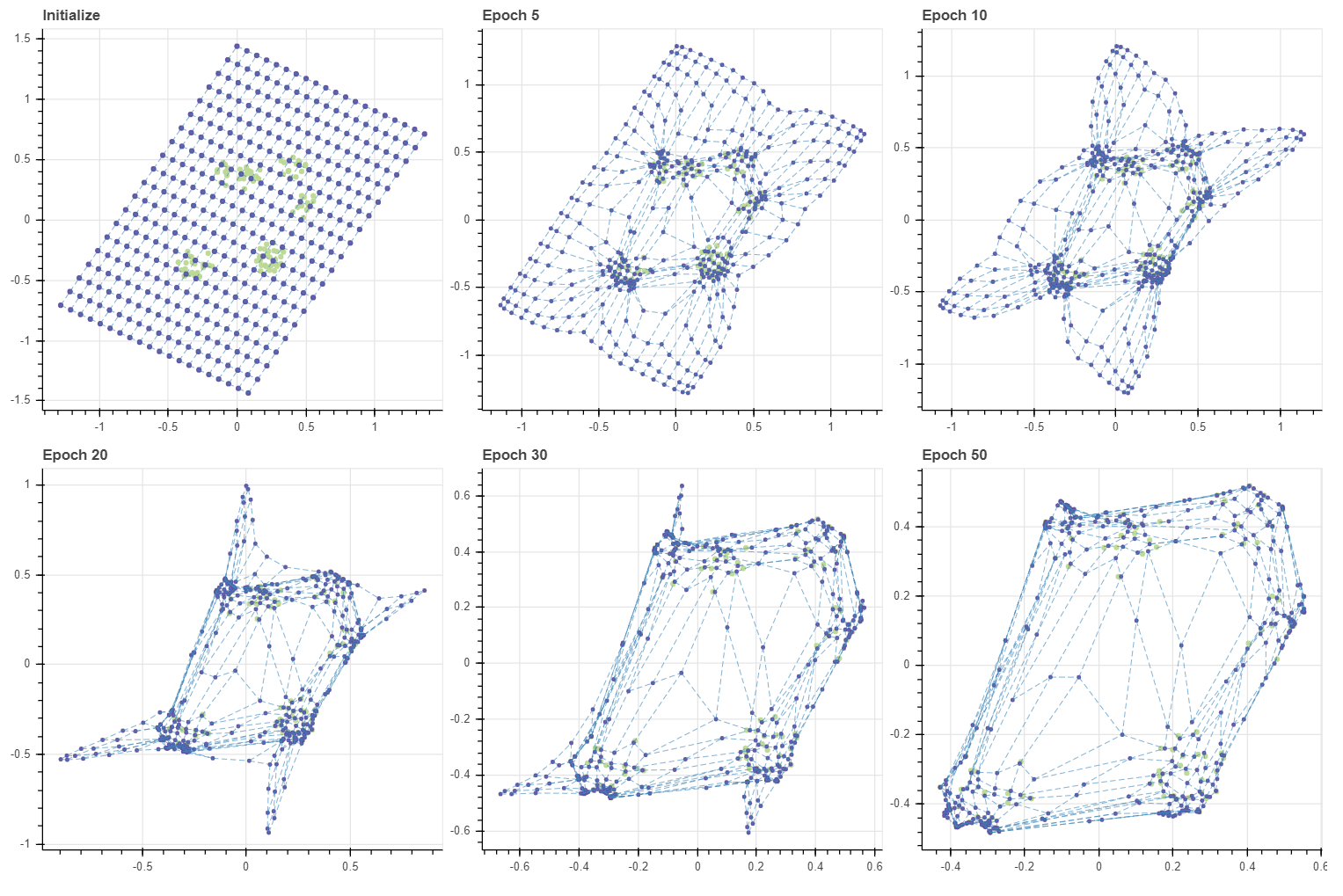
마스크를 곱하는 방식이 직관적이지만 그리드가 커지면 학습이 매우 비효율적입니다. update_cmeans 함수는 gradient 가 0 이 아닌 마디들만을 선택하여 효율적으로 계산을 합니다. 그리고 수렴한 SOM 의 마디는 해당 마디가 BMU 혹은 그 이웃으로 할당된 학습데이터의 가중 평균 근처로 이동하므로, 역으로 이를 이용하여 c-means 와 비슷하게 gradient 를 정의합니다. 또한 BMU 와 거리가 너무 멀어 업데이트가 잘 되지 않는 마디들의 학습을 가속화 하기 위하여 마디 주변이 변화하면 그 변화를 다음 반복 단계에서 따라가도록 유도함으로써 수렴이 빠르게 일어나도록 하였습니다.
Relation with k-means
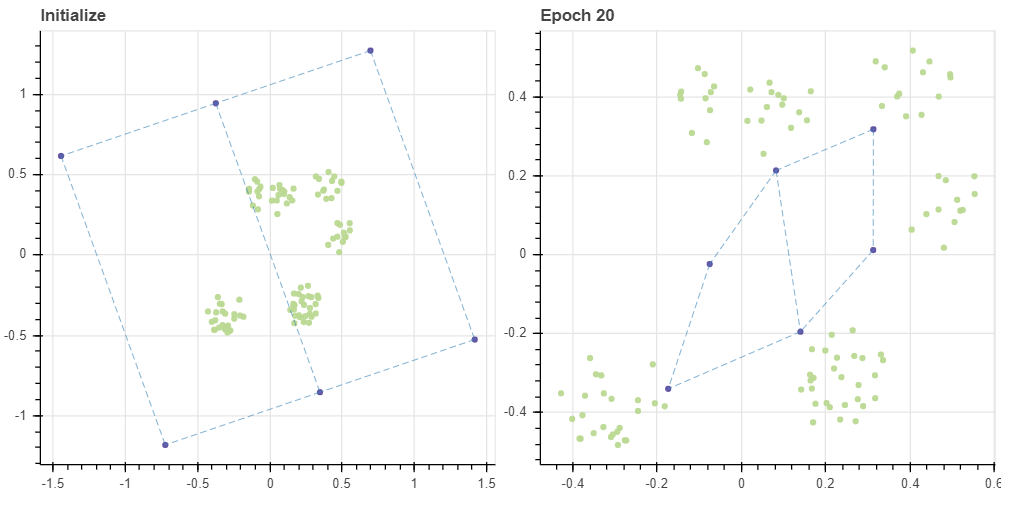
이번 포스트에서는 SOM 의 개념을 알아보고 이를 간단히 구현하였습니다. 그리고 SOM 은 그리드의 초기값에 따라 학습 수렴 속도와 품질이 차이가 날 수 있음도 살펴보았습니다. 만약 마디의 개수가 데이터의 개수보다 훨씬 작다면 SOM 은 k-means 와 비슷하게 학습됩니다. 아래처럼 (2, 3) 의 그리드의 마디는 데이터를 약 다섯개의 군집으로 표현합니다. (0,1) 마디를 제외한 모든 마디는 BMU 로 할당 되기 때문에 마치 k-means 의 centroid 의 역할을 합니다. 그런데 이 BMU 에 해당하는 데이터의 평균값으로 마디의 값이 학습 되기 때문에 실제 데이터에 존재하지 않는 공간에 마디가 위치하는 현상이 발생하기도 합니다. 이는 k-means 에서도 자주 발생하는 문제이기도 합니다. 그리고 이때는 데이터 공간을 몇 개의 partitions 으로 나눕니다. 하지만 공간의 구조를 학습하지는 않습니다. 반대로 그리드의 크기가 어느 정도 크면 데이터 분포의 외각 뿐 아니라 구조까지도 자세하게 학습합니다. 여유가 될 경우 빈 공간까지도 학습할 수 있습니다. 또한 그리드의 크기는 고차원 지도의 resolution 의 역할을 하기도 합니다. 이에 대해서는 다음 포스트에서 다뤄봅니다.
Appendix
fit 함수를 구현할 때 update_func 에 metric argument 를 이용할 수 있도록 하였습니다. metric 은 scipy.spatial 에서 제공하는 모든 거리 척도를 이용할 수 있습니다. 이번에는 데이터의 일부를 제거하여 방향 벡터 기준으로 군집이 생기는 초승달 모양의 데이터를 만든 뒤, Cosine distance 를 이용하여 SOM 을 학습해 봅니다. 방향 벡터 기준으로는 Euclidean distance 를 이용하는 것보다 훨씬 간단한 공간이기 때문에 빠르게 수렴이 일어납니다.
X, _ = make_rectangular_clusters(n_clusters=8, min_size=10, max_size=15, volume=0.2, seed=0)
X -= 0.5
X = X[np.where(X[:,0] >= -0.19)[0]]
grid, C, pairs = initialize(X, 6, 6, method='grid', tiny=0.1)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=10, draw_each=2, epsilon=-0.1, metric='cosine',
decay=False, update_func=update_cmeans, lr=0.5, grid=grid, adjust_ratio=0)
show(gp)
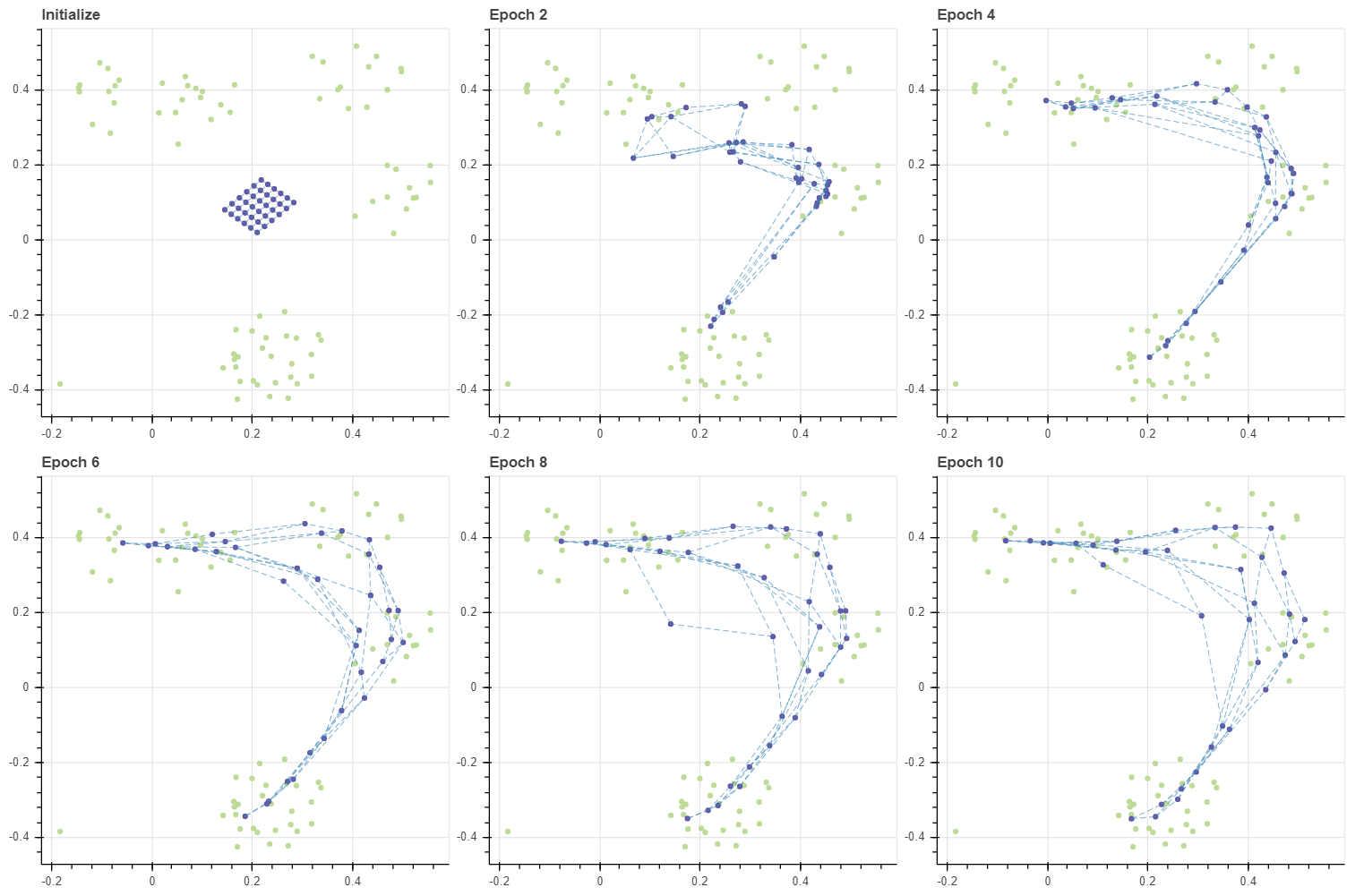
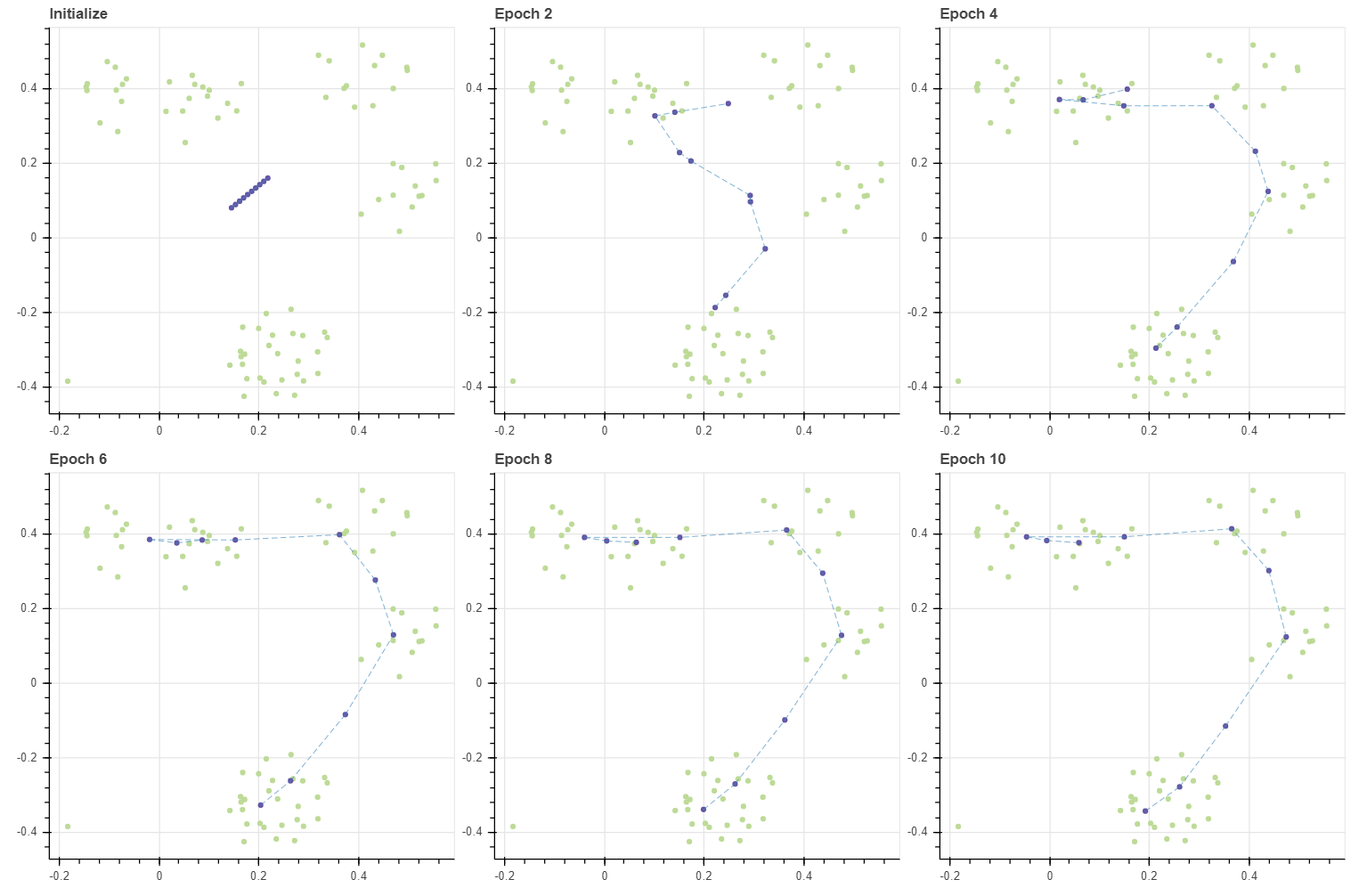
Cosine distance 를 이용하면 모든 벡터를 반지름이 1 인 구 (sphere) 의 표면 위에 위치하는 단위 벡터 (unit vector) 로 변형한 뒤 거리를 측정하는 것과 같습니다. Cosine distance 가 벡터의 크기 (norm) 에 영향을 받지 않기 때문입니다. 그렇다면 격자 모양의 grid 보다 훨씬 단순한 공간을 가정해야 합니다. 2차원 데이터에서의 각도는 1차원 변수이기 때문입니다. 3차원에서는 2 개의 각도로 데이터를 표현합니다. 이러한 좌표 표기법을 극좌표계 (radial coordinate system) 이라 합니다. 여하튼 이번에는 선으로 이뤄진 그리드를 가정하여 데이터를 학습합니다.
grid, C, pairs = initialize(X, 1, 10, method='grid', tiny=0.1)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=10, draw_each=2, epsilon=-0.1, metric='cosine',
decay=False, update_func=update_cmeans, lr=0.5, grid=grid, adjust_ratio=0)
show(gp)
방향을 따라 이어지는 선의 형태로 그리드가 학습되었습니다. 필요에 따라서는 circular 형태의 grid 를 만들 수도 있습니다. 이때는 neighbors, inv_neighbors 를 만드는 함수를 추가로 정의하면 됩니다.
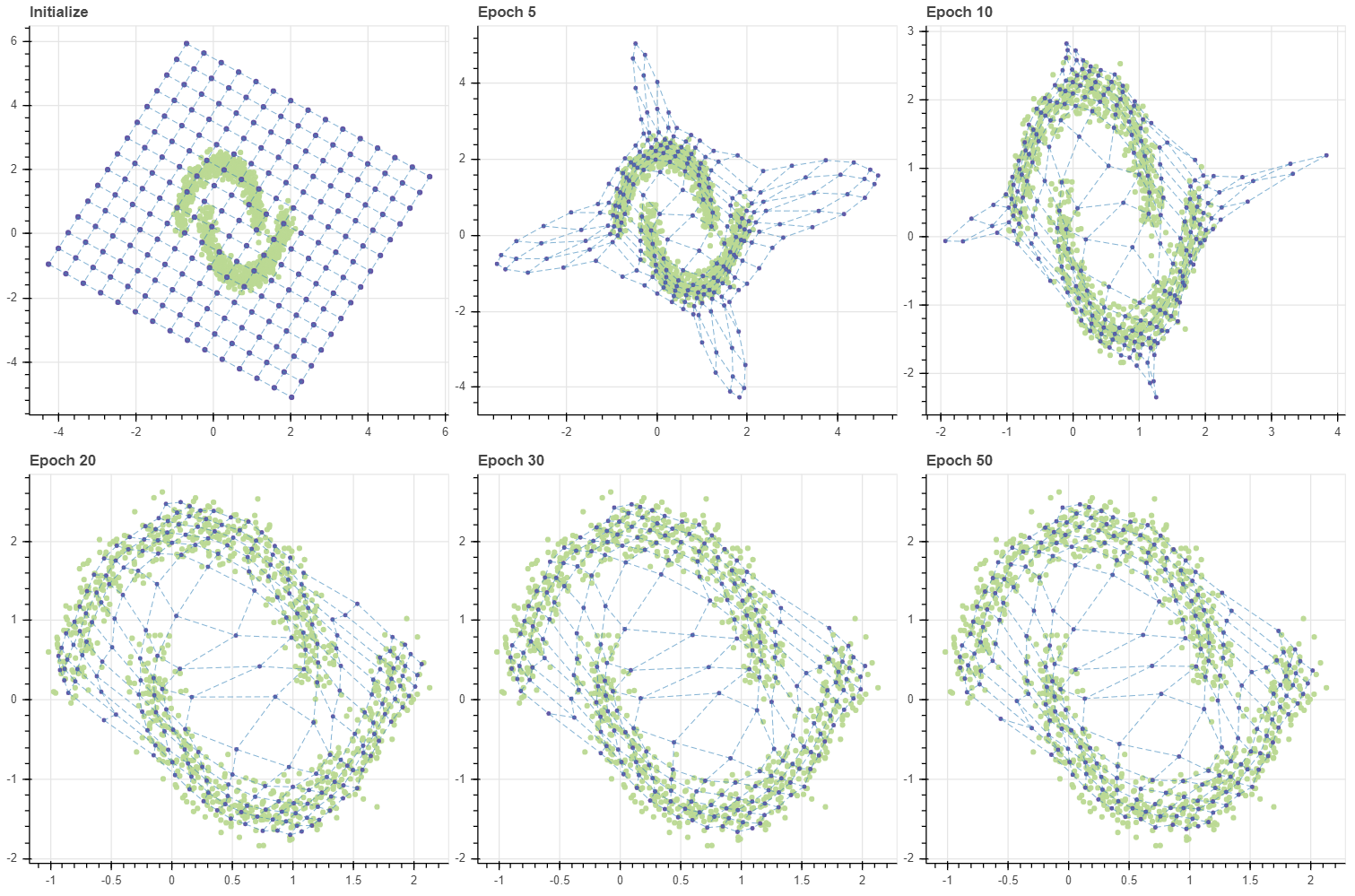
마지막으로 지금까지 만든 구현체를 이용하여 two moon datset 에 (15,15) 그리드의 SOM 을 학습해 봅니다. 1000 개의 데이터에 대하여 225 개의 마디가 달라붙습니다. 이번에도 적은 epochs 만에 학습이 안정화 됨을 볼 수 있습니다.
from soydata.data.classification import make_moons
from soydata.visualize import scatterplot
X, labels = make_moons(n_samples=1000, xy_ratio=2.0, x_gap=-0.2, y_gap=0.2, noise=0.1)
grid, C, pairs = initialize(X, 15, 15, method='grid', tiny=2.0)
masks = make_masks(grid)
gp = fit_with_draw(X, C, epochs=50, draw_each=[5, 5, 10, 10, 20], epsilon=-0.1,
decay=False, update_func=update_cmeans, lr=0.5, grid=grid, adjust_ratio=0.5)
show(gp)