PageRank 는 대표적인 graph ranking 알고리즘입니다. 이전 포스트에서 Python 의 자료구조인 dict 를 이용하여 PageRank 를 구현하였습니다. 하지만 Python 의 불필요한 작업들 때문에 속도가 빠르지 않습니다. C 를 기반으로 구현된 numpy 를 이용하면 매우 빠른 PageRank 구현체를 만들 수 있습니다. 그러나 잘못 구현하면 out of memory 를 만나게 됩니다. 이번 포스트에서는 numpy 를 이용한 PageRank 의 구현에 관하여 이야기합니다.
Brief review of PageRank
PageRank 는 가장 대표적인 graph ranking 알고리즘입니다. Web page graph 에서 중요한 pages 를 찾는데 이용됩니다. 이를 위하여 PageRank 는 직관적인 아이디어를 이용합니다. 많은 유입 링크 (backlinks)를 지니는 pages 가 중요한 pages 라 가정하였습니다. 일종의 ‘투표’입니다. 각 web page 가 다른 web page 에게 자신의 점수 중 일부를 부여합니다. 다른 web page 로부터의 링크 (backlinks) 가 많은 page 는 자신에게 모인 점수가 클 것입니다.
PageRank 에서 각 node 의 중요도 는 다음처럼 계산됩니다. 는 page 의 backlinks 의 출발점 마디입니다. 에서 로 web page 의 hyperlink 가 있습니다. 각 page 는 자신의 점수를 자신이 가진 links 의 개수만큼으로 나눠서 각각의 에게 전달합니다. 는 로부터 받은 점수의 합에 상수 를 곱합니다. 그리로 전체 마디의 개수 의 역수인 의 배 만큼을 더합니다.
자세한 PageRank 의 이야기는 이전 포스트를 참고하세요.
Implementing PageRank with Python dict (slow version)
이전 포스트에서 Python 의 dict 를 이용하여 PageRank 를 구현하였습니다. input 데이터 g 는 dict dict 형식입니다. Pure Python codes 로 구현할 수 있습니다. 쓰지 못할 수준은 아니지만, 계산 속도가 느린 편입니다.
def pagerank(G, bias=None, df=0.15,
max_iter=50, converge_error=0.001,verbose=0):
"""
Arguments
---------
G: Inbound graph, dict of dict
G[to_node][from_node] = weight (float)
df: damping factor, float. default 0.15
"""
if not bias:
bias = {}
A, nodes = _normalize(G)
N = len(nodes) # number of nodes
sr = 1 - df # survival rate (1 - damping factor)
ir = 1 / N # initial rank
# Initialization
rank = {n:ir for n in nodes}
# Iteration
for _iter in range(1, max_iter + 1):
rank_new = {}
# t: to node, f: from node, w: weight
for t in nodes:
f_dict = A.get(t, {})
rank_t = sum((w*rank[f] for f, w in f_dict.items())) if f_dict else 0
rank_t = sr * rank_t + df * bias.get(t, ir)
rank_new[t] = rank_t
# convergence check
diff = sum((abs(rank[n] - rank_new[n]) for n in nodes))
if diff < converge_error:
if verbose:
print('Early stopped at iter = {}'.format(_iter))
break
if verbose:
print('Iteration = {}'.format(_iter))
rank = rank_new
return rank이전 포스트에서 이용하였던 영화 - 배우 네트워크를 이용합니다. 총 265,607 개의 마디로 이뤄진 그래프 입니다. Edges 는 ‘영화 배우’ 와 ‘영화 배우’의 양방향으로 연결되어 있습니다.
len(g) # 265607g 는 inbound graph 입니다.
g[from_node u][to_node v] = transaction prob (v --> u)
bias 는 관객수를 이용하였습니다. 네이버 영화 데이터베이스 기준 영화평이 많이 달린 영화에 가중치를 주는 personalized PageRank 입니다. Bias 의 합은 1이 되도록 영화평 개수의 총합으로 정규화를 하였습니다.
데이터는 저의 pagerank github 에 올려두었습니다.
# create idx to num comments
with open('pagerank/data/movie-actor/num_comments.txt', encoding='utf-8') as f:
docs = [line[:-1].split('\t') for line in f]
_idx2numcomments = {movie_idx:int(num) for movie_idx, num in docs}
bias = [0, 0, ... 374, 0, 5572, ... ]
_sum = sum(bias)
bias = np.asarray([b / _sum for b in comments_bias])영화평의 개수를 bias 로 이용했습니다. 한국에서 인기있던 영화들의 rank 가 높아야 합니다. 영화 nodes 만을 선택한 뒤, 랭킹이 높은 상위 50 개의 영화를 살펴봅니다.
movie_rank = {node:rank for node, rank in rank.items() if node[0] == 'm'}
for movie, _ in sorted(movie_rank.items(), key=lambda x:-x[1])[:50]:
movie_idx = movie.split()[1]
print(idx2movie(movie_idx))한국에서 인기있는 영화들이 상위에 랭킹이 된 것으로 보아 PageRank 알고리즘은 학습이 잘 되었음을 확인할 수 있습니다.
인천상륙작전 (2016, 한국)
연평해전 (2015, 한국)
국가대표 (2009, 한국)
설국열차 (2013, 한국)
어벤져스: 에이지 오브 울트론 (2015, 미국)
국제시장 (2014, 한국)
겨울왕국 (2014, 미국)
암살 (2015, 한국)
7번방의 선물 (2013, 한국)
캡틴 아메리카: 시빌 워 (2016, 미국)
곡성(哭聲) (2016, 한국)
귀향 (2016, 한국)
26년 (2012, 한국)
인터스텔라 (2014, 미국 영국)
세 얼간이 (2011, 인도)
부산행 (2016, 한국)
아가씨 (2016, 한국)
레미제라블 (2012, 영국)
밀정 (2016, 한국)
럭키 (2016, 한국)
디 워 (2007, 한국)
판도라 (2016, 한국)
미스터 고 (2013, 한국)
다세포 소녀 (2006, 한국)
해운대 (2009, 한국)
님아, 그 강을 건너지 마오 (2014, 한국)
광해, 왕이 된 남자 (2012, 한국)
수상한 그녀 (2014, 한국)
트랜스포머: 사라진 시대 (2014, 미국)
킹스맨 : 시크릿 에이전트 (2015, 미국 영국)
괴물 (2006, 한국)
아수라 (2016, 한국)
역린 (2014, 한국)
포화 속으로 (2010, 한국)
어거스트 러쉬 (2007, 미국)
비긴 어게인 (2014, 미국)
검은 사제들 (2015, 한국)
아바타 (2009, 미국)
말할 수 없는 비밀 (2008, 대만)
베테랑 (2015, 한국)
덕혜옹주 (2016, 한국)
감기 (2013, 한국)
타워 (2012, 한국)
라스트 갓파더 (2010, 한국 미국)
늑대소년 (2012, 한국)
왕의 남자 (2005, 한국)
그래비티 (2013, 미국 영국)
영웅: 샐러멘더의 비밀 (2013, 한국 미국 러시아 연방)
라디오 스타 (2006, 한국)
과속스캔들 (2008, 한국)
Implementing PageRank with Numpy (fast version)
먼저 dict dict 형식인 g 를 sparse matrix 로 변환합니다. 다음 round 의 rank 값은 현재 rank 값에 adjacent matrix 를 내적한 형태입니다. 그림처럼 adjacent matrix 의 번째 row 와 현재 시점의 를 내적한 값이 에 저장됩니다.
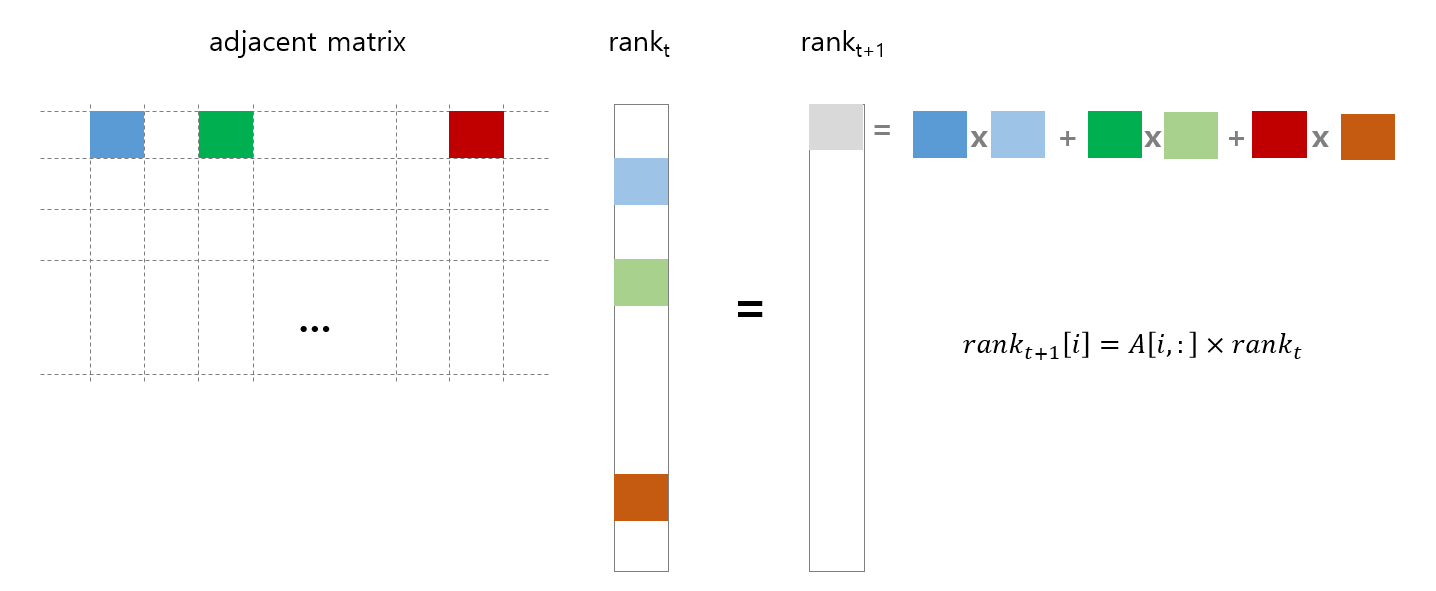
Row 는 이전 포스트에서 개미로 비유한 random walker 가 다음 시점에 이동할 마디이며, column 은 이전 시점에 출발한 마디입니다. g 를 돌며 from node idx 를 rows list 에, to node idx 를 column list 에, 그리고 weight 를 data list 에 입력하여 csc_matrix 로 만듭니다.
Sparse matrix 에 관한 설명은 이전 포스트를 참고하세요.
from scipy.sparse import csc_matrix
rows = []
cols = []
data = []
for from_node, to_dict in g.items():
from_idx = node2idx[from_node]
for to_node, weight in to_dict.items():
to_idx = node2idx[to_node]
rows.append(from_idx)
cols.append(to_idx)
data.append(weight)
A = csc_matrix((data, (rows, cols)))이렇게 만들어진 adjacent matrix 의 shape 은 아래와 같습니다. 마디의 개수는 len(g) 와 같습니다.
print(A.shape) # (265607, 265607)ir 은 입니다. PageRank 계산을 시작할 때 모든 마디의 기본값으로 이용됩니다. 를 위하여 adjacent matrix 와 rank vector 의 내적을 수행해야 합니다.
이 때 numpy.dot 을 이용할 수 있습니다. 하지만, numpy 는 sparse matrix 의 내적을 수행하기 위해 이를 dense matrix 로 변환합니다. 265,607 by 265,607 의 double array 를 만듭니다. 계산을 하기 이전에 out of memory 가 발생합니다.
# Do not implement like this
# You will open the door to hell
# np.dot(A, rank) Scipy 에서는 scipy.sparse 에서 safe_sparse_dot 함수를 제공합니다. scipy.sparse.matrix 와 numpy.ndarray 의 내적, 혹은 sparse matrix 간의 내적은 scipy 의 함수를 이용해야 합니다. sparse matrix 에서 제공하는 .dot() 함수는 safe_sparse_dot 함수를 호출합니다.
# call scipy.sparse safe_sparse_dot()
rank_new = A.dot(rank) Sparse matrix 와 dense matrix 간의 내적은 sparse matrix 의 0 이 아닌 값을 기준으로 계산해야 합니다. Sparse matrix 의 대부분의 값이 0 이기 때문에 곱셈을 할 필요가 없는 값이 매우 많기 때문입니다. safe_sparse_dot() 함수는 이를 위하여 만들어졌습니다.
간혹 내적의 총합이 float 연산 과정에서의 truncated error 때문에 1 보다 줄어들 수 있습니다. 이를 보정하기 위하여 l1 normalize 를 수행합니다.
print(rank_new.sum()) # 0.9997310802270433
rank_new = normalize(rank_new.reshape(1, -1), norm='l1').reshape(-1)
print(rank_new.sum()) # 1.0000000000000002Dangling nodes 문제를 방지하기 위한 random jumping 까지 구현되어야 합니다. 에 의하여 계산된 에 배를 한 뒤, 를 더합니다.
이 과정을 모두 포함한 구현은 아래와 같습니다.
import numpy as np
max_iter = 30
df = 0.85
ir = 1 / A.shape[0]
rank = np.asarray([ir] * A.shape[0])
bias = np.asarray(bias)
for n_iter in range(1, max_iter + 1):
rank_new = A.dot(rank) # call scipy.sparse safe_sparse_dot()
rank_new = normalize(rank_new.reshape(1, -1), norm='l1').reshape(-1)
rank_new = df * rank_new + (1 - df) * bias
diff = abs(rank - rank_new).sum()
rank = rank_new
print('iter {} : diff = {}'.format(n_iter, diff))영화평의 개수를 bias 로 이용했습니다. 한국에서 인기있던 영화들의 rank 가 높아야 합니다. 영화 nodes 만을 선택한 뒤, 랭킹이 높은 상위 50 개의 영화를 살펴봅니다.
for movie, value in sorted(movierank.items(), key=lambda x:-x[1])[:50]:
movie_idx = movie.split()[1]
print(idx2movie(movie_idx))한국에서 인기있는 영화들이 상위에 랭킹이 된 것으로 보아 PageRank 알고리즘은 학습이 잘 되었음을 확인할 수 있습니다.
26년 (2012, 한국)
부산행 (2016, 한국)
디 워 (2007, 한국)
곡성(哭聲) (2016, 한국)
7번방의 선물 (2013, 한국)
인터스텔라 (2014, 미국 영국)
인천상륙작전 (2016, 한국)
국제시장 (2014, 한국)
괴물 (2006, 한국)
국가대표 (2009, 한국)
암살 (2015, 한국)
베테랑 (2015, 한국)
아바타 (2009, 미국)
연평해전 (2015, 한국)
설국열차 (2013, 한국)
말할 수 없는 비밀 (2008, 대만)
겨울왕국 (2014, 미국)
왕의 남자 (2005, 한국)
캡틴 아메리카: 시빌 워 (2016, 미국)
님아, 그 강을 건너지 마오 (2014, 한국)
늑대소년 (2012, 한국)
귀향 (2016, 한국)
과속스캔들 (2008, 한국)
어벤져스: 에이지 오브 울트론 (2015, 미국)
세 얼간이 (2011, 인도)
다세포 소녀 (2006, 한국)
검사외전 (2016, 한국)
아저씨 (2010, 한국)
군도:민란의 시대 (2014, 한국)
광해, 왕이 된 남자 (2012, 한국)
해적: 바다로 간 산적 (2014, 한국)
해운대 (2009, 한국)
터널 (2016, 한국)
화려한 휴가 (2007, 한국)
아가씨 (2016, 한국)
럭키 (2016, 한국)
다크 나이트 라이즈 (2012, 미국 영국)
다이빙벨 (2014, 한국)
덕혜옹주 (2016, 한국)
아수라 (2016, 한국)
다크 나이트 (2008, 미국)
밀정 (2016, 한국)
인셉션 (2010, 미국 영국)
포화 속으로 (2010, 한국)
전우치 (2009, 한국)
검은 사제들 (2015, 한국)
히말라야 (2015, 한국)
트랜스포머 (2007, 미국)
7광구 (2011, 한국)
좋은 놈, 나쁜 놈, 이상한 놈 (2008, 한국)
Comparison computation time: Python dict vs Numpy
numpy 를 이용하여 구현한 PageRank 의 iteration 30 번의 계산 시간은 0.278 초 입니다.
Python dict 를 이용하여 구현한 PageRank 의 iteration 30 번의 계산 시간은 42.706 초 입니다.
압도적으로 numpy 가 빠름을 확인할 수 있습니다. CPU 를 이용한 행렬 연산을 Python 으로 해야한다면, Python 의 자료구조가 아닌 numpy 와 scipy 를 이용하면 빠른 계산을 할 수 있습니다.
계산 속도 비교의 jupyter notebook tutorial 은 github 에 올려두었습니다. 실험에 이용한 데이터와 함께 있으니 직접 비교하실 수 있습니다.
한국에서 유명한 영화들이 높은 rank 를 갖는 것은 맞지만, 두 방법의 rank 기준 순서가 조금 다릅니다. Graph 내의 PageRank 의 합을 1 로 정하여 truncation error 가 난 것인지 혹은 구현 과정에서 실수가 있었는지는 살펴봐야 겠습니다.