NMF, k-means 를 이용한 토픽 모델링과 NMF, k-means + PyLDAvis 시각화

LDAvis 는 토픽 모델링의 한 방법인 Latent Dirichlet Allocation (LDA) 의 학습 결과를 시각화하는 목적으로 자주 이용됩니다. 하지만 LDAvis 는 임의의 토픽 모델링의 결과를 모두 시각화 할 수 있습니다. 이번 포스트에서는 LDA 외에 토픽 모델링에 이용되는 Nonnegative Matrix Factorization (NMF) 와 k-means 의 학습 결과를 LDA 의 학습 결과와 유사하게 변형한 뒤, LDAvis 를 이용하여 이를 시각화 하는 방법에 대하여 살펴봅니다.

LDAvis

Latent Dirichlet Allocation (LDA) 는 토픽 모델링에 이용되는 대표적인 알고리즘입니다. 여기서 말하는 토픽은 “어떤 주제를 구성하는 단어들”입니다. 추상적인 정의입니다. 흔히 우리가 말하는 “이 글의 주제”와 같습니다. 한 토픽을 설명하기 위하여 특정 단어들이 이용될 것입니다. 문서 집합에서 이 단어 집합을 찾으려는 것이 토픽 모델링입니다. 일종의 word-level semantic clustering 입니다.

LDA 는 세 가지 가정을 합니다. 첫째, “문서는 여러 개의 토픽을 지닐 수 있고 한 문서는 특정 토픽을 얼마나 지녔는지의 확률 벡터로 표현된다” 입니다. 이 말은 아래와 같은 식으로 기술됩니다. $t$ 는 토픽, $d$ 는 문서입니다.

$$P(t \vert d)$$

둘째, “하나의 토픽은 해당 토픽에서 이용되는 단어의 비율로 표현된다” 입니다. 이는 아래와 같은 각 토픽 별 단어의 생성 확률 분포 식으로 표현됩니다. $w$ 은 단어입니다.

$$P(w \vert t)$$

그리고 한 문서에서 특정 단어들이 등장할 가능성 $P(w, d)$ 은 위의 두 확률 분포의 곱으로 표현됩니다. 아래의 식은 문서 $d$ 에 단어 $w = w_1, w_2, \dots$ 가 등장할 확률입니다. $C$ 는 Dirichlet distribution 에 의한 상수이며, $n^{w_j, d}$ 는 문서 $d$ 에서 단어 $w_j$ 가 등장한 횟수입니다.

$$P(w, d) = C \times \sum_{w_j \in w} n^{w_j, d} \prod_i P(w_j \vert t_i) \times P(t_i \vert d)$$

그리고 LDA 의 학습 결과로 각 문서에 대한 토픽 벡터 $P_{dt}$ 와 토픽에 대한 단어 벡터 $P_{tw}$ 를 얻습니다. LDAvis 는 이 두 가지 정보와 원 데이터를 이용하여 토픽 모델링의 결과를 시각화 합니다.

고차원의 벡터를 이해하기 위하여 시각화 방법들이 이용됩니다. 대표적인 방법으로 t-SNE 라 불리는 t-Stochastic Neighbor Embedding 이 있습니다. t-SNE 는 고차원 공간에서 유사한 두 벡터가 2 차원 공간에서도 유사하도록, 원 공간에서의 점들 간 유사도를 보존하면서 차원을 축소합니다. 우리가 이해할 수 있는 공간은 2 차원 모니터 (지도) 혹은 3 차원의 공간이기 때문입니다. 그리고 LDA 의 학습 결과로 얻은 두 가지 정보인 $P_{dt}$ 와 $P_{tw}$ 도 고차원의 벡터입니다. 단지 확률 벡터이기 때문에 각 row 의 합이 1 이고, 모든 값이 0 이상일 뿐입니다.

LDAvis 는 두 가지 정보를 시각적으로 표현합니다. 첫째는 2차원으로 표현된 $P_{tw}$ 입니다. 토픽에 대한 단어 벡터는 방향적 경향성이 있기 때문에 Principal Component Analysis (PCA) 를 이용할 수도 있습니다. 혹은 t-SNE 를 이용할 수도 있습니다. LDAvis 는 이 두 가지 알고리즘 중 하나를 선택하여 $P_{tw}$ 를 2 차원의 벡터로 표현합니다.

둘째로 각 토픽에 대한 키워드를 선택합니다. 키워드 점수는 한 토픽에 얼마나 자주 등장하는지에 대한 점수와 다른 토픽보다 유독 많이 등장하는가에 대한 점수를 $\lambda$ 의 비율로 합하여 정의합니다. 이에 대한 의미는 이전의 LDAvis 에 대한 포스트를 참고 하시기 바랍니다. 식은 아래와 같으며 $\lambda$ 는 사용자에 의하여 설정 가능합니다.

$$\lambda \cdot P(w \vert t) + (1 - \lambda) \cdot \frac{P(w \vert t)}{P(w)}$$

아래는 LDAvis 가 이용하는 인풋 데이터입니다. LDA 의 학습 결과 외에도 각 문서의 길이, 단어 인덱스를 단어로 치환하는 list of str, 그리고 각 단어의 전체 빈도수 벡터가 입력됩니다. 이 포스트에서는 lovit_textmining_dataset 을 이용하여 LDA, NMF, k-means 를 이용한 토픽 모델링 학습과 LDAvis 를 이용한 이들의 시각화를 알아봅니다.

topic_term_dists # numpy.ndarray, shape = (n_topics, n_terms)
doc_topic_dists  # numpy.ndarray, shape = (n_docs, n_topics)
doc_lengths      # numpy.ndarray, shape = (n_docs,)
vocab            # list of str, vocab list
term_frequency   # numpy.ndarray, shape = (n_vocabs,)

LDA 의 구현체 중 가장 널리 이용되는 것은 아마도 Python 의 Gensim 일 것입니다. 그리고 많은 경우 Gensim LDA 를 시각화 하기 위하여 LDAvis 가 이용되기 때문에 PyLDAvis 에는 gensim 용 함수를 따로 만들어 두었습니다. 아래는 Bag of words model 로 표현된 데이터를 이용하여 Gensim LDA 를 학습한 뒤, LDAvis 로 시각화 하는 과정의 코드입니다. Gensim LDA 는 dict 형식으로 된 int -> str 의 dictionary 가 필요합니다. Gensim 의 Dictionary 는 실제 텍스트 파일에서 단어의 빈도수와 document frequency 를 계산하여 생성됩니다. 하지만 다른 목적을 위하여 이미 벡터라이징이 끝나있는 경우들도 많습니다. 이 코드는 이러한 상황을 가정하였습니다. 그러므로 Gensim 의 Dictionary 를 만들기 위하여 다시 한 번 텍스트 파일을 이용하지는 않을 겁니다 (심지어 scikit-learn 의 Vectorizer 와 Gensim 의 Dictionay 에서의 vocabulary 순서가 다를 수도 있습니다). 아래처럼 sparse matrix 와 vocabulary index 를 가지고 있을 때 Dictionary 의 대용은 enumerate 와 dict 함수를 이용하여 list of str 로부터 손쉽게 만들 수 있습니다.

import gensim # version=3.6.0
from gensim.models import LdaModel
import pyLDAvis # version=2.1.1
import pyLDAvis.gensim as gensimvis
from lovit_textmining_dataset.navernews_10days import get_bow

# input data
x, idx_to_vocab, vocab_to_idx = get_bow(date='2016-10-20', tokenize='noun')
x # sparse matrix
idx_to_vocab # list of str

# train Gensim LDA
corpus = gensim.matutils.Sparse2Corpus(x, documents_columns=False)
id2word = dict(enumerate(idx_to_vocab))
lda_model = LdaModel(corpus=corpus, num_topics=100, id2word=id2word)

# make dictionary
dictionary = dict(enumerate(idx_to_vocab))

# train LDAvis
prepared_data = gensimvis.prepare(lda_model, corpus, dictionary)
pyLDAvis.show(prepared_data)

혹은 dict (int, str) 형식이 아닌 gensim 의 Dictionary 를 직접 만들 수도 있습니다. Dictionary 에는 여섯 종류의 attributes 가 포함되어 있는데, 이들은 모두 bag of words 와 같은 sparse matrix 와 각 column 이 어떤 단어에 해당하는지에 대한 인덱스로부터 만들 수 있는 정보들입니다. 물론 LDAvis 만을 학습하기 위해서는 위처럼 dict(enumerate(idx_to_vocab)) 만으로도 충분합니다.

from gensim.corpora import Dictionary

def bow_to_dictionary(bow, idx_to_vocab):
    id2token = dict(enumerate(idx_to_vocab))
    token2id = {token:id for id, token in id2token.items()}
    num_docs, num_pos = bow.shape
    _, cols = bow.nonzero()
    dfs = np.bincount(cols, minlength=num_pos)
    dfs = dict(enumerate(dfs.tolist()))
    num_nnz = x.nnz

    dictionary = Dictionary()
    dictionary.id2token = id2token
    dictionary.token2id = token2id
    dictionary.num_docs = num_docs
    dictionary.num_pos = num_pos
    dictionary.dfs = dfs
    dictionary.num_nnz = num_nnz
    return dictionary

dictionary = bow_to_dictionary(x, idx_to_vocab)

그 결과 예시는 아래와 같습니다.

위의 결과도 해석이 가능하고 납득도 됩니다. 하지만 LDA 모델을 제대로 이용하기 위해서는 몇 가지 후처리 과정이 필요합니다. 이에 대해서는 이후에 다른 포스트에서 다루도록 하겠습니다.

Topic modeling using Nonnegative Matrix Factorization (NMF)

Nonnegative Matrix Factorization (NMF) 은 Latent Semantic Indexing (LSI) 와 비슷합니다. LDA 는 각 문서를 토픽 벡터로 표현합니다. 하지만 LSI 는 topic space 의 벡터로 표현하며, LSI 는 Doc2Vec 과 비슷합니다. Doc2Vec 으로 학습된 문서에 대한 벡터는 그 값을 해석하기는 어렵지만, 비슷한 벡터로 표현되는 두 문서는 서로 비슷한 토픽을 지녔다고 해석할 수 있습니다. 이처럼 NMF 역시 문서를 topic space 의 벡터로 표현합니다. 하지만 그 벡터의 각 elements 가 모두 0 이상인 값으로 구성되어 있습니다.

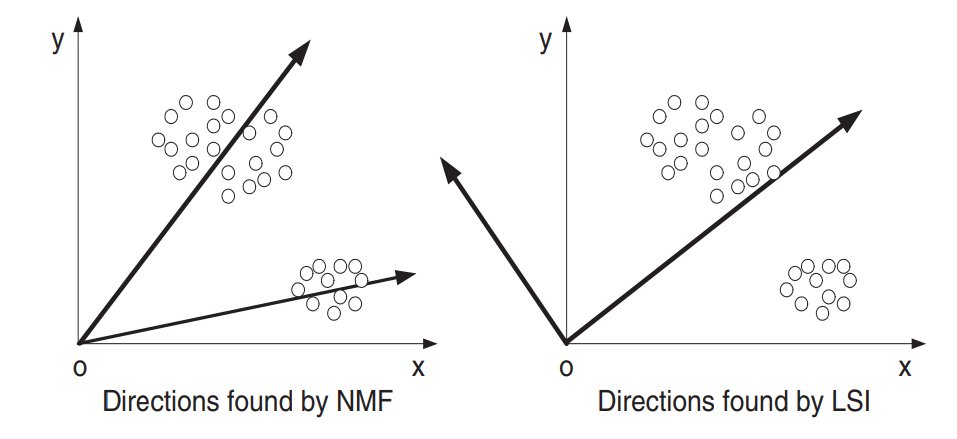
하지만 NMF 는 Singular Vector Decomposition (SVD) 를 이용하는 LSI 와 기본 가정이 다릅니다. 아래 그림은 (Xu et al., 2003) 의 NMF 에 대한 개념도입니다. LSI 는 각 토픽을 나타내는 새로운 축들이 서로 독립이라 가정하며, 벡터 공간에서 두 벡터가 독립이기 위해서는 서로 간의 각도가 90 도여야 합니다. 그리고 한 벡터와 직교인 다른 벡터는 음의 방향 벡터를 가질 가능성이 “매우” 높습니다. 하지만 우리가 토픽 모델링에 이용할 Bag-of-words model 은 가장 작은 값이 0 인 nonnegative matrix 이며, 음의 값으로 이뤄진 토픽 벡터는 의미를 해석하기 어렵습니다.

이러한 직교 가정을 풀어버린 matrix factorization 방법이 NMF 입니다. 각 토픽을 나타내는 축이 서로 독립이 아니라 가정합니다. 그 결과 비슷한 두 개의 축이 학습될 수는 있습니다. 하지만 LSI 보다 훨씬 더 큰 해석력을 가집니다.

NMF 는 아래의 식으로부터 두 가지 성분을 학습합니다. $D$ 는 Sparse coding 의 dictionary 역할을 하며, 토픽 모델링에서는 각 토픽의 단어 벡터 입니다. $Y$ 는 $D$ 를 이용하는 각 문서의 새로운 토픽 벡터 입니다. $y$ 는 각 문서 $x$ 가 $D$ 의 성분을 얼마나 지니고 있는지 표현하는 coefficient vector 입니다.

$$min \rVert X - DY \rVert_{Fro}^{2}, D \ge 0 \& Y \ge 0$$

그리고 여기에 과적합을 해결하기 위한 L1, L2 regularization 을 추가할 수 있습니다. Scikit-learn 의 NMF 구현체는 두 가지 regularization 에 대하여 모두 구현되어 있습니다. $\gamma$ 는 L1, L2 penalty 를 상대적으로 얼마나 줄지 조절하는 패러매터입니다. $\gamma$ 가 1 이면 Sparse coding 입니다.

$$min \rVert X - DY \rVert_{Fro}^{2} + \alpha \times \gamma \times (\rVert D \rVert_1 + \rVert Y \rVert_1) + 0.5 \cdot \alpha \times (1 - \gamma ) \times (\rVert D \rVert_2 + \rVert Y \rVert_2), D \ge 0 \& Y \ge 0$$

위의 해를 탐색하기 위해서는 PCA 와 비슷한 해법이 이용됩니다. 하지만 우리가 학습해야 하는 패러매터는 $D, Y$ 두 가지 입니다. 이러한 상황에서 이용할 수 있는 해법 중 하나는 하나의 변수를 고정하고 다른 변수를 학습하는 것입니다. 처음에는 $D, Y$ 를 임의의 값으로 초기화 한 뒤, $D$ 를 고정하여 최적의 $Y$ 를 찾습니다. 하나의 변수를 고정하면 Least Square Estimation 을 이용할 수 있습니다. 여기에 nonnegativity 까지 고려할 수 있는 추정 방법을 이용하여 해를 탐색합니다 (Constrained least square estimation methods). 그러나 아직 $D$ 는 학습이 되지 않은 값입니다. 이번에는 $Y$ 를 고정한 뒤 위와 동일한 과정으로 $D$ 를 학습합니다. 이러한 과정을 두 값이 수렴할 때까지 반복합니다.

참고로 Scikit-learn 의 Sparse Coding 은 구현체가 완성되지 않았습니만, NMF 는 거의 완성되었습니다. 위의 식의 해를 찾기 위해서는 많은 계산량이 필요하기 때문에 대부분 근사 해법이 이용되지만, Scikit-learn 의 Sparse coding 은 이를 이용하지 않는 것으로 생각됩니다. 대신 NMF 는 근사 해법을 이용하고 있기 때문에 빠른 시간 내에 학습이 가능합니다. 만약 Sparse coding 이 필요할 경우에는 $\gamma$ 만 1 로 설정하면 됩니다.

아래는 Bag of words model 에 NMF 를 적용하여 각 문서 별 topic vector 를 학습하는 과정입니다. 문서마다 길이가 다를 수 있으니 L1 normalization 을 거쳐 입력 데이터로 사용합니다. Scikit-learn 에서는 $\gamma$ 가 l1_ratio 라는 이름의 패러매터로 구현되어 있습니다. 그리고 기본값은 0 입니다. 오로직 L2 regularization 만 적용됩니다.

from sklearn.decomposition import NMF
from sklearn.preprocessing import normalize
from lovit_textmining_dataset.navernews_10days import get_bow

x, idx_to_vocab, vocab_to_idx = get_bow(date='2016-10-20', tokenize='noun')

n_topics = 100
n_docs, n_terms = x.shape

nmf = NMF(n_components=n_topics)
y = nmf.fit_transform(normalize(x, norm='l1')) # shape = (n_docs, n_topics)
components = nmf.components_ # shape = (n_topics, n_terms)

y 는 각 문서에 대한 토픽 벡터 입니다. 단 nonnegative topical vector 이지만 확률 형식은 아닙니다 (그 합이 1 은 아닙니다). components 는 각 토픽에 대한 단어 벡터이며, 이 역시 확률 형식은 아닙니다. 앞서서 LDAvis 는 확률 형식으로 정의된 $P_{dt}, P_{tw}$ 가 필요하다고 말하였습니다. 우리는 y 와 components 를 확률 형식으로 변환하여 LDAvis 에 입력할 것입니다. 그런데 y 의 경우 빈 문서가 입력될 수도 있습니다. Zero vector $x$ 는 zero vector $y$ 로 변환되며, 이는 normalize 함수를 적용하여도 여전이 zero vector 입니다. 이 경우에는 모든 값을 1 / n_topics 로 입력하였습니다. 이 과정을 zero_to_base_prob 라는 함수로 구현합니다.

import numpy as np
from sklearn.preprocessing import normalize

def y_to_doc_topic(y):
    n_topics = y.shape[1]
    base = 1 / n_topics
    doc_topic_prob = normalize(y, norm='l1')
    rowsum = doc_topic_prob.sum(axis=1)
    doc_topic_prob[np.where(rowsum == 0)[0]] = base
    return doc_topic_prob

components 에 zero vector 가 학습될 가능성은 낮지만, 안전하게 위와 동일한 후처리 과정을 거쳐 L1 normalization 을 합니다.

def components_to_topic_term(components):
    n_terms = components.shape[1]
    base = 1 / n_terms
    topic_term_prob = normalize(components, norm='l1')
    rowsum = topic_term_prob.sum(axis=1)
    topic_term_prob[np.where(rowsum) == 0)[0]] = base
    return topic_term_prob

doc_topic_prob = y_to_doc_topic(y)
topic_term_prob = components_to_topic_term(components)

문서 길이와 단어 빈도수 벡터는 Bag-of-words model 을 행과 열 방향으로 합하여 얻을 수 있습니다. sum 함수의 결과를 numpy.ndarray 로 변환하는 부분만 추가하여 아래처럼 두 변수를 만들 수 있습니다.

doc_lengths = np.asarray(x.sum(axis=1)).reshape(-1)
term_frequency = np.asarray(x.sum(axis=0)).reshape(-1)

이제 모든 재료가 준비되었으니 LDAvis 에 이를 입력합니다. R 은 오른쪽에 출력되는 키워드의 개수입니다.

from pyLDAvis import prepare, show

prepared_data = prepare(
    topic_term_prob,
    doc_topic_prob,
    doc_lengths,
    idx_to_vocab,
    term_frequency,
    R = 30 # num of displayed terms
)

show(prepared_data)

사실 NMF 는 $\gamma$ 에 따라 학습 결과의 경향이 달라지기 때문에 이 역시 잘 설정해야 합니다. 이에 대한 내용은 이후에 다른 포스트에서 다루도록 하겠습니다.

Topic modeling using k-means

LDA 는 한 문서가 한 개 이상의 토픽으로 구성될 수 있다고 가정합니다. 하지만 하나의 문서에 반드시 하나의 토픽만 할당될 수 있다면 k-means 와 같은 문서 군집화 방법도 이용될 수 있습니다. 이전의 LDAvis 를 이용한 k-means 시각화포스트에서는 포스트에서 제안한 centroid vector 를 이용한 k-means clustering labeling 의 결과를 시각화 하기 위하여 복잡한 과정을 거쳤습니다. 만약 LDAvis 의 키워드 추출 방식을 이용한다면 이보다 손쉽게 LDAvis 를 이용하여 k-means 의 학습 결과를 시각화 할 수 있습니다.

문서 군집화를 위해서는 Euclidean distance 가 아닌 Cosine distance 를 이용하는 것이 좋다는 것을 이전의 Spherical k-means 포스트에서 언급하였습니다. 이전 포스트에서 언급한 soyclustering 패키지를 이용하여 Spherical k-means 를 학습합니다. 참고로 LDA 나 NMF 는 하나의 문서에 여러 개의 토픽이 포함될 수 있다 가정하기 때문에 토픽의 개수가 작더라도 문서가 토픽 벡터로 잘 표현됩니다. 하지만 k-means 에서는 여러 이유로 상대적으로 좀 더 큰 숫자를 군집의 개수로 입력하는 것이 좋습니다. 이 이유에 대해서도 나중에 k-means 에 대한 포스트에서 설명하겠습니다. 또한 학습에 이용하는 Bag-of-words model 에서 stopwords 를 성실히 제거하지 않았을 경우에는 TF-IDF 를 적용하는 것도 괜찮은 방법입니다. 이번에는 TF-IDF 로 변환한 데이터를 이용하여 문서 군집화를 학습합니다.

from sklearn.feature_extraction.text import TfidfTransformer
from soyclustering import SphericalKMeans
from lovit_textmining_dataset.navernews_10days import get_bow

x, idx_to_vocab, vocab_to_idx = get_bow(date='2016-10-20', tokenize='noun')
x_tfidf = TfidfTransformer().fit_transform(x)

kmeans = SphericalKMeans(n_clusters = 200)
labels = kmeans.fit_predict(x_tfidf)

이번에도 우리는 문서의 토픽 확률 벡터와 토픽의 단어 확률 벡터를 만들어야 합니다. labels 는 각 문서가 어떤 군집 (토픽)에 해당하는지에 대한 아이디이며, 이를 이용하여 손쉽게 문서의 토픽 확률 벡터를 만들 수 있습니다. labels 에 해당하는 토픽에 1 의 확률을 부여하면 됩니다.

import numpy as np

def labels_to_doc_topic_prob(labels):
    n_clusters = np.unique(labels).shape[0]
    n_docs = labels.shape[0]
    doc_topic_prob = np.zeros((n_docs, n_clusters))

    for c in range(n_clusters):
        idx = np.where(labels == c)[0]
        doc_topic_prob[idx, c] = 1

    return doc_topic_prob

토픽의 단어 확률 벡터는 각 label 에 해당하는 문서 내의 단어 빈도수 벡터를 정규화 하면 됩니다. 이때도 빈 문서가 하나의 군집이 될 수 있으니 NMF 에서와 동일한 후처리 과정을 거칩니다.

def labels_x_to_topic_term_prob(labels, x):
    n_clusters = np.unique(labels).shape[0]
    n_terms = x.shape[1]

    topic_term_prob = np.zeros((n_clusters, n_terms))
    for c in range(n_clusters):
        idx = np.where(labels == c)[0]
        topic_term_freq = x[idx].sum(axis=0)
        freq_sum = topic_term_freq.sum()
        if freq_sum == 0:
            continue
        topic_term_prob[c] = topic_term_freq / freq_sum

    base = 1 / n_terms
    rowsum = topic_term_prob.sum(axis=1)
    topic_term_prob[np.where(rowsum == 0)[0]] = base

    return topic_term_prob

NMF 와 같은 과정을 거쳐 LDAvis 의 입력값을 모두 마련합니다. 그 뒤 다시 한 번 prepared data 를 만들어 시각화를 합니다. 만약 t-SNE 를 이용하여 2 차원의 토픽 벡터를 학습하고 싶다면 아래처럼 mds 옵션을 tsne 로 변환해 줍니다. 그리고 두 축의 이름도 아래처럼 변경할 수 있습니다.

from pyLDAvis import prepare, show

doc_topic_prob = labels_to_doc_topic_prob(labels)
topic_term_prob = labels_x_to_topic_term_prob(labels, x)
doc_lengths = np.asarray(x.sum(axis=1)).reshape(-1)
term_frequency = np.asarray(x.sum(axis=0)).reshape(-1)

prepared_data = prepare(
    topic_term_prob,
    doc_topic_prob,
    doc_lengths,
    idx_to_vocab,
    term_frequency,
    mds = 'tsne',
    plot_opts = {'xlab': 't-SNE1', 'ylab': 't-SNE2'}
)

show(prepared_data)

Reference

• Xu, W., Liu, X., & Gong, Y. (2003, July). Document clustering based on non-negative matrix factorization. In Proceedings of the 26th annual international ACM SIGIR conference on Research and development in informaion retrieval (pp. 267-273). ACM.